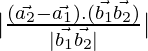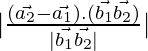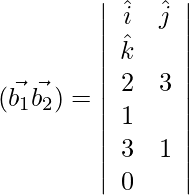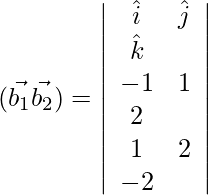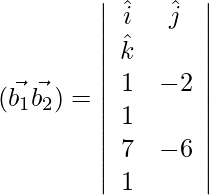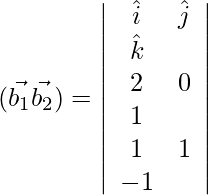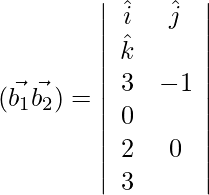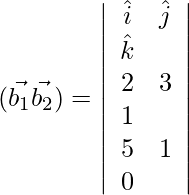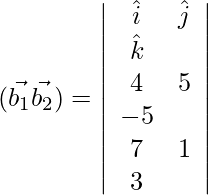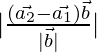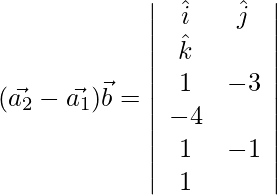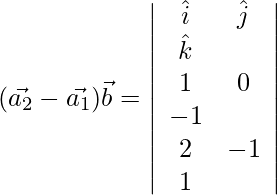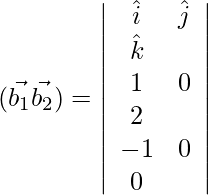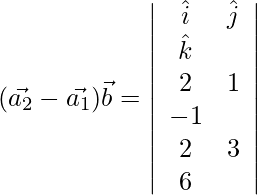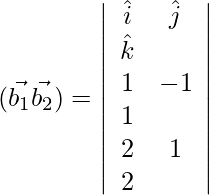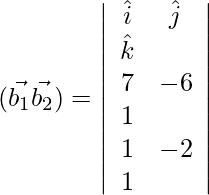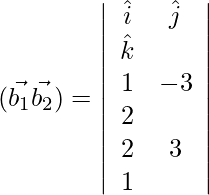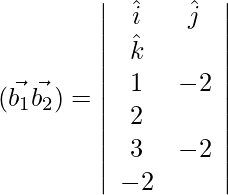Pregunta 1. Encuentra la distancia más corta entre el par de líneas cuya ecuación vectorial es:
(yo) 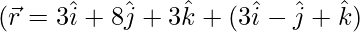 y
y 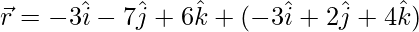
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
=
=
=
= 36 + 225 + 9
= 270
=
= √270
Al sustituir los valores en la fórmula, tenemos
DE = 270/√270
= √270
La distancia más corta entre el par de líneas dado es 3√30 unidades.
(ii) 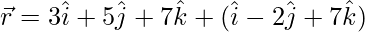 y
y 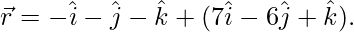
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
=
=
=
= – 16 × 32
= – 512
=
=
Al sustituir los valores en la fórmula, tenemos
DE =
La distancia más corta entre el par de líneas dado es
unidades.
(iii) 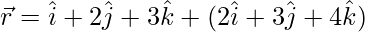 y
y 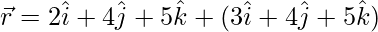
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
=
=
= 1
=
Al sustituir los valores en la fórmula, tenemos
DE =
La distancia más corta entre el par de líneas dado es 1/√6 unidades.
(iv) 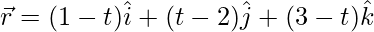 y
y 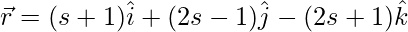
Solución:
Las ecuaciones anteriores se pueden reescribir como:
y,
Como sabemos que la distancia más corta entre las líneas
y
es:
re =
= 9/3√2
La distancia más corta es 3/√2 unidades.
(v) 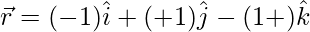 y
y 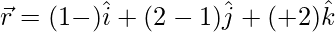
Solución:
Las ecuaciones dadas se pueden escribir como:
\
y
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
= 15
= 3√2
Por lo tanto, la distancia entre las líneas es
unidades.
(vi) 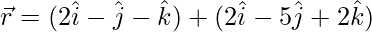 y
y 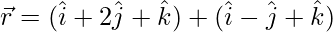
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re =
Ahora,
= 3√2
Sustituyendo los valores en la fórmula, tenemos
La distancia entre las líneas es
unidades.
(vii) 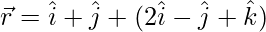 y
y 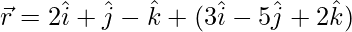
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
= 10
Sustituyendo los valores en la fórmula, tenemos:
La distancia entre las líneas es 10/√59 unidades.
(viii) 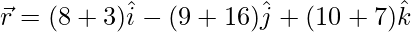 y
y 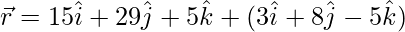
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
= 1176
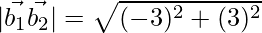
= 84
Sustituyendo los valores en la fórmula, tenemos:
La distancia entre las líneas es 1176/84 = 14 unidades.
Pregunta 2. Encuentra la distancia más corta entre el par de líneas cuya ecuación cartesiana es:
(yo) 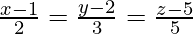 y
y 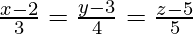
Solución:
Las líneas dadas se pueden escribir como:
y
=
=
= –1
= √6
Al sustituir los valores en la fórmula, tenemos:
SD = 1/√6 unidades.
(ii) 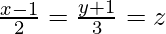 y
y 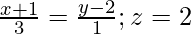
Solución:
Las ecuaciones dadas también se pueden escribir como:
y \
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
= 3
SD = 3/√59 unidades.
(iii) 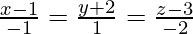 y
y 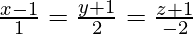
Solución:
Las ecuaciones dadas se pueden reescribir como:
y
= √29
= 8
SD = 8/√29 unidades.
(iv) 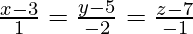 y
y 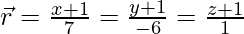
Solución:
Las ecuaciones dadas se pueden reescribir como:
y
=
SD = 58/√29 unidades.
Pregunta 3. Al calcular la distancia más corta, determine si los pares de líneas se intersecan o no:
(yo) 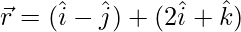 y
y 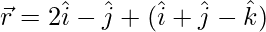
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
= –1
= √14
⇒ DE = 1/√14 unidades ≠ 0
Por lo tanto, el par de líneas dado no se interseca.
(ii) 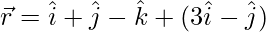 y
y 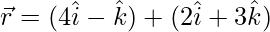
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
= 0
= √94
⇒ DE = 0/√94 unidades = 0
Por lo tanto, el par de líneas dado se intersecan.
(iii) 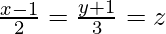 y
y 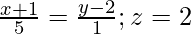
Solución:
Las líneas dadas se pueden reescribir como:
y
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
= −9
= √195
⇒ DE = 9/√195 unidades ≠ 0
Por lo tanto, el par de líneas dado no se interseca.
(iv) 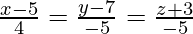 y
y 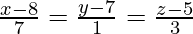
Solución:
Las líneas dadas se pueden reescribir como:
y
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
= 282
⇒ DE = 282/√3 unidades ≠ 0
Por lo tanto, el par de líneas dado no se interseca.
Pregunta 4. Encuentra la distancia más corta entre los siguientes:
(yo) 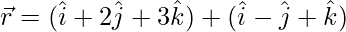 y
y 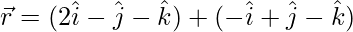
Solución:
La segunda línea dada se puede reescribir como:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
=
⇒ DE =
unidades.
(ii) 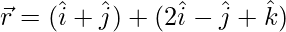 y
y 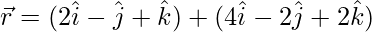
Solución:
La segunda línea dada se puede reescribir como:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
⇒
= √11
⇒ DE = √11/√6 unidades.
Pregunta 5. Encuentra las ecuaciones de las líneas que unen los siguientes pares de vértices y luego encuentra la distancia más corta entre las líneas:
(i) (0, 0, 0) y (1, 0, 2) (ii) (1, 3, 0) y (0, 3, 0)
Solución:
La ecuación de la recta que pasa por los vértices (0, 0, 0) y (1, 0, 2) viene dada por:
De manera similar, la ecuación de la recta que pasa por los vértices (1, 3, 0) y (0, 3, 0):
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
= −6
= 2
⇒ DE = |-6/2| = 3 unidades.
Pregunta 6. Escriba las ecuaciones vectoriales de las siguientes líneas y, por lo tanto, encuentre la distancia más corta entre ellas:
Solución:
Las ecuaciones dadas se pueden escribir como:
y
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
⇒
=
\vec{|b|}= 7
⇒ DE = √293/7 unidades.
Pregunta 7. Encuentra la distancia más corta entre los siguientes:
(yo) 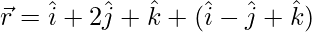 y
y 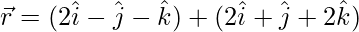
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
=
=
= 3√2
⇒ DE = 3/√2 unidades.
(ii) 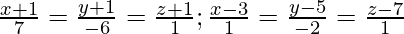
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
=
= √116
⇒ DE = 2√29 unidades.
(iii) 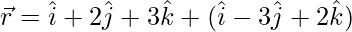 y
y 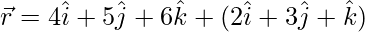
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
=
= √171
⇒ DE = 3√19 unidades.
(iv) 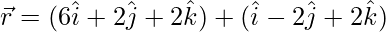 y
y 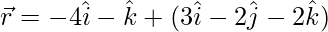
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
Ahora,
=
(\vec{a_2}-\vec{a_1}).(\vec{b_1}×\vec{b_2})=108
|\vec{b_1}×\vec{b_2}|=\sqrt{(-9)^2+(3)^2+(9)^2}
= 12
⇒ DE = 9 unidades.
Pregunta 8. Encuentra la distancia entre las líneas: 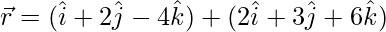 y
y 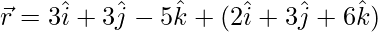
Solución:
Como sabemos que la distancia más corta entre las rectas
y
es:
re=
=
⇒
= √293
⇒ DE = √293/7 unidades.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA