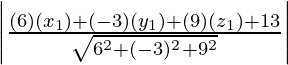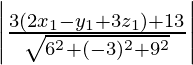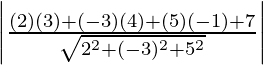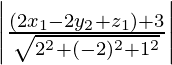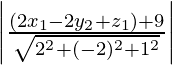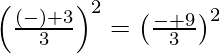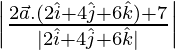Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.10

Pregunta 1. Encuentra la distancia entre los planos paralelos 2x – y + 3z – 4 = 0 y 6x – 3y + 9z + 13 = 0

Solución:

Sea P(x ₁ , y ₁ , z ₁ ) cualquier punto en el plano 2x – y + 3z – 4 = 0.

⟹ 2x ₁ – y ₁ + 3z ₁ = 4 (ecuación-1)

Distancia entre (x ₁ , y ₁ , z ₁ ) y el plano

6x – 3y + 9z + 13 = 0:

Como sabemos, la distancia del punto (x ₁ , y ₁ , z ₁ ) al plano π: ax + by + cz + d = 0 viene dada por:

p = $\left|\frac{ax_1+by_1+cz_1+d}{\sqrt{a^2+b^2+c^2}}\right|$

Ahora, sustituimos los valores, obtenemos

p = $\left|\frac{(6)(x_1)+(-3)(y_1)+(9)(z_1)+13}{\sqrt{6^2+(-3)^2+9^2}}\right|$

= $\left|\frac{3(2x_1-y_1+3z_1)+13}{\sqrt{6^2+(-3)^2+9^2}}\right|$

= $\left|\frac{3(4)+13}{3\sqrt{14}}\right|$ [usando la ecuación 1]

= $\frac{25}{3\sqrt{14}}$

Por lo tanto, la distancia entre los planos paralelos 2x – y + 3z – 4 = 0 y 6x – 3y + 9z + 13 = 0 son $\frac{25}{3\sqrt{14}}$ unidades.

Pregunta 2. Encuentra la ecuación del plano que pasa por el punto (3, 4, -1) y es paralelo al plano 2x – 3y + 5z + 7 = 0. Encuentra también la distancia entre los dos planos.

Solución:

Como el plano es paralelo a 2x – 3y + 5z + 7 = 0, debe ser de la forma:

2x – 3y + 5z + θ = 0

Se da que,

El avión pasa por (3, 4, –1)

⟹ 2(3) – 3(4) +5(–1) + θ = 0

θ = -11

De este modo,

La ecuación del plano es la siguiente:

2x – 3y + 5z – 11 = 0

Distancia del plano 2x – 3y + 5z + 7 = 0 desde (3, 4, –1):

Como sabemos, la distancia del punto (x ₁ , y ₁ , z ₁ ) al plano π: ax + by + cz + d = 0 viene dada por:

p = $\left|\frac{ax_1+by_1+cz_1+d}{\sqrt{a^2+b^2+c^2}}\right|$

Ahora, después de sustituir los valores, obtendremos

= $\left|\frac{(2)(3)+(-3)(4)+(5)(-1)+7}{\sqrt{2^2+(-3)^2+5^2}}\right|$

= $\frac{4}{\sqrt{38}}$

Por lo tanto, la distancia del plano 2x – 3y + 5z + 7 = 0 a (3, 4, -1) es $\frac{4}{\sqrt{38}}$

Pregunta 3. Encuentra la ecuación del plano medio paralelo a los planos 2x – 2y + z + 3 = 0 y 2x – 2y + z + 9 = 0

Solución:

Dado:

Ecuación de planos:

π ₁ = 2x – 2y + z + 3 = 0

π ₂ = 2x – 2y + z + 9 = 0

Sea la ecuación del plano semiparalelo a estos planos:

π ₃ : 2x – 2y + z + θ = 0

Ahora,

Sea P(x ₁ , y ₁ , z ₁ ) cualquier punto de este plano,

⟹ 2(x ₁ ) – 2(y ₁ ) + (z ₁ ) + θ = 0 —(ecuación-1)

Como sabemos, la distancia del punto (x ₁ , y ₁ , z ₁ ) al plano π: ax + by + cz + d = 0 viene dada por:

p = $\left|\frac{ax_1+by_1+cz_1+d}{\sqrt{a^2+b^2+c^2}}\right|$

Distancia de P a π ₁ :

p = $\left|\frac{(2x_1-2y_2+z_1)+3}{\sqrt{2^2+(-2)^2+1^2}}\right|$

= $\left|\frac{(-θ)+3}{3}\right|$ (Usando la ecuación 1)

Similarmente,

Distancia de q a π ₂ :

q = $\left|\frac{(2x_1-2y_2+z_1)+9}{\sqrt{2^2+(-2)^2+1^2}}\right|$

= $\left|\frac{(-θ)+9}{3}\right|$ (Usando la ecuación 1)

Como π ₃ es medio paralelo es π ₁ y π ₂ :

p = q

Asi que,

$\left|\frac{(-θ)+3}{3}\right|=\left|\frac{-θ +9}{3}\right|$

Ahora cuadrados en ambos lados, obtenemos

$\left(\frac{(-θ)+3}{3}\right)^2=\left(\frac{-θ+9}{3}\right)^2$

(3 – θ) ² = (9 – θ) ²

9 – 2×3×θ + θ ² = 81 – 2×9×θ + θ ²

θ = 6

Ahora, sustituimos el valor de θ = 6 en la ecuación 2x – 2y + z + θ = 0, obtenemos

Por lo tanto, la ecuación del plano paralelo medio es 2x – 2y + z + 6 = 0

Pregunta 4. Encuentra la distancia entre los planos 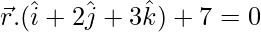$\vec{r}.(\hat{i}+2\hat{j}+3\hat{k})+7=0$ y $\vec{r}.(2\hat{i}+4\hat{j}+6\hat{k})+7=0$

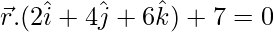
Solución:

Sea $\vec{a}$ el vector de posición de cualquier punto P en el plano

$\vec{r}(\hat{i}+2\hat{j}+3\hat{k})+7=0$

Asi que,

$\vec{a}(\hat{i}+2\hat{j}+3\hat{k})+7=0$ —(ecuación 1)

Como sabemos, la distancia entre $\vec{a}$ el plano y el plano $\vec{r}.\vec{n}-d=0$ viene dada por:

p = $\left|\frac{\vec{a}.\vec{n}-d}{|n|}\right|$

La longitud de la perpendicular desde $P(\vec{a}) to plane \vec{r}.(2\hat{i}+4\hat{j}+6\hat{k})+7=0$ se obtiene sustituyendo los valores de $\vec{a}\ and\ \vec{n}$ , obtenemos

p = $\left|\frac{2\vec{a}.(2\hat{i}+4\hat{j}+6\hat{k})+7}{|2\hat{i}+4\hat{j}+6\hat{k}|}\right|$

= $\left|\frac{2\vec{a}.(\hat{i}+2\hat{j}+3\hat{k})+7}{\sqrt{2^2+4^2+6^2}}\right|$

= $\left|\frac{2(-7)+7}{\sqrt{56}}\right|$

p = $\frac{7}{\sqrt{56}}$

Por lo tanto, la distancia entre los planos

$\vec{r}.(\hat{i}+2\hat{j}+3\hat{k})+7=0$ y $\vec{r}.(2\hat{i}+4\hat{j}+6\hat{k})+7=0$ es $\frac{7}{\sqrt{56}}$