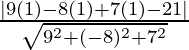Pregunta 14. Encuentra la ecuación del plano que pasa por la intersección de los planos x – 2y + z = 1 y 2x + y + z = 8 y paralelo a la recta con relaciones de dirección proporcionales a 1, 2, 1. Además, encuentra la distancia perpendicular de (1, 1, 1) desde este plano.
Solución:
Como sabemos que la ecuación del plano que pasa por la recta de intersección de dos planos es
(un 1 X + segundo 1 y + C 1 z + re 1 ) + λ(un 2 X + segundo 2 y + C 2 z + re 2 ) = 0
Entonces, la ecuación del plano que pasa por la intersección de los planos x – 2y + z = 1 y 2x + y + z = 8 es
(1 + 2λ)x + (-2 + λ)y + (1 + λ)z – 1 – 8λ = 0 ….(1)
Además, dado que este plano es paralelo a la recta cuyas relaciones de dirección son proporcionales a 1, 2, 1.
⇒ (1 + 2λ)1 + (-2 + λ)2 + (1 + λ)1 = 0
⇒ 1 + 2λ – 4 + 2λ + 1 + λ = 0
⇒ 5λ – 2 = 0
⇒ λ = 2/5
Ahora pon el valor de λ en (1), tenemos:
9x – 8y + 7z – 21 = 0 es la ecuación requerida.
Y la distancia perpendicular del plano desde (1, 1, 1) es
=
=
unidades.
Pregunta 15. Muestra cuándo la recta 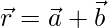 es paralela al plano
es paralela al plano 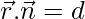 . Demuestra que la recta
. Demuestra que la recta 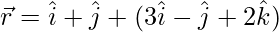 es paralela al plano
es paralela al plano 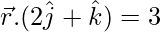 . Además, encuentre la distancia entre la línea y el plano.
. Además, encuentre la distancia entre la línea y el plano.
Solución:
El plano pasa por el punto con vector de posición
y es paralelo al vector
Dada la ecuación del plano es
o
Entonces, el vector normal es
y d = 3.
Ahora,
= 0 – 2 + 2 = 0
Entonces,
es perpendicular a
Por tanto, la recta dada es paralela al plano dado.
Como sabemos que la distancia entre la recta y el plano paralelo es la distancia entre cualquier punto de la recta y el plano dado.
Entonces, Distancia(d) =
=
=
unidades.
Pregunta 16. Demuestra que la recta 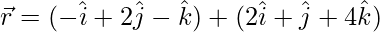 es paralela al plano
es paralela al plano 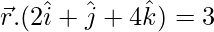 . Además, encuentre la distancia entre los dos.
. Además, encuentre la distancia entre los dos.
Solución:
El plano pasa por el punto con el vector de posición
y es paralelo al vector
[Tex]\vec{b}[/Tex]
El plano dado es
o
Entonces, el vector normal es
y d = 3.
Ahora,
= 0 – 2 + 2 = 0
Entonces, es perpendicular a
.
Por tanto, la recta dada es paralela al plano.
Como sabemos que la distancia entre una recta y un plano paralelo es la distancia entre cualquier punto de la recta y el plano dado.
entonces, Distancia(d) =
=
= 1/√6 unidades.
Pregunta 17. Encuentra la ecuación del plano que pasa por la intersección de los planos 3x – 4y + 5z = 10 y 2x + 2y – 3z = 4 y paralelo a la recta x = 2x = 3z.
Solución:
Como sabemos que la ecuación del plano que pasa por la recta de intersección de dos planos es
(un 1 X + segundo 1 y + C 1 z + re 1 ) + λ(un 2 X + segundo 2 y + C 2 z + re 2 ) = 0
Entonces, la ecuación del plano pasa por la intersección de la
planos 3x – 4y + 5z = 10 y 2x + 2y – 3z = 4 es
(3 + 2λ)x + (-4 + 2λ)y + (5 – 3λ)z – 10 – 4λ = 0 ….(1)
Dado que la ecuación de recta es x = 2x = 3z.
Ahora, dividiendo esta ecuación por 6, obtenemos,
Entonces obtenemos que las relaciones de dirección de esta línea son proporcionales a 6, 3, 2.
Ahora, la normal al plano es perpendicular a la recta cuyas relaciones de dirección son 6, 3, 2.
⇒ (3 + 2λ)6 + (-4 + 2λ)3 + (5 – 3λ)2 – 10 – 4λ = 0
⇒ λ = -4/3
Ahora ponga el valor de λ en la ecuación (1), obtenemos,
x – 20y + 27z = 14 es la ecuación requerida.
Pregunta 18. Encuentra las formas vectorial y cartesiana de la ecuación del plano que pasa por el punto (1, 2, -4) y es paralelo a las rectas 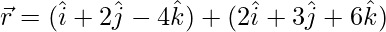 y
y 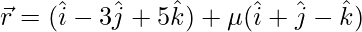 . Además, encuentre la distancia del punto desde el plano obtenido.
. Además, encuentre la distancia del punto desde el plano obtenido.
Solución:
Dado que las ecuaciones de las rectas son
Como sabemos que la ecuación vectorial de un plano que pasa por un punto
y es paralelo a
y
es
Asi que,
Ahora, la ecuación vectorial del plano es
La ecuación cartesiana del plano es
-9x + 8y – z = 11
Ahora la distancia del punto (9, -8, -10) al plano es
re = √146
Pregunta 19. Encuentra la ecuación del plano que pasa por los puntos (3, 4, 1) y (0, 1, 0) y paralelo a la recta 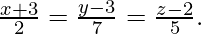
Solución:
Cuando el plano pasa por los puntos (3, 4, 1), entonces la ecuación del plano es
a(x – 3) + b(y – 4) + c(z – 1)=0 ….(1)
Cuando este plano pasa por los puntos (0, 1, 0), entonces la ecuación del plano es
a(0 – 3) + b(1 – 4) + c(0 – 1) = 0
⇒ 3a + 3b + 3c = 0 …..(2)
Además, dado que el plano (es decir, eq (1)) es paralelo a la línea.
Entonces, la normal del plano (es decir, eq (1)) es perpendicular a la línea, entonces,
2a + 7b + 5c = 0 …..(3)
Ahora, al resolver las ecuaciones (1), (2) y (3), obtenemos
8x – 13y + 15z + 13 = 0 es la ecuación requerida.
Pregunta 20. Halla las coordenadas del punto donde la recta 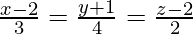 e interseca al plano x – y + z – 5 = 0. Halla también el ángulo entre la recta y el plano.
e interseca al plano x – y + z – 5 = 0. Halla también el ángulo entre la recta y el plano.
Solución:
Dado que la ecuación de la recta es
⇒ x = 3λ + 2, y = 4λ – 1, z = 2λ + 2 ….(1)
Como sabemos que (x, y, z) intersecan el plano x – y + z – 5 = 0,
Asi que,
3λ + 2 – (4λ – 1) + 2λ + 2 – 5 = 0
⇒ λ = 0
Ahora, pon este valor en la ecuación (1), obtenemos
x = 2, y = -1, z = 2
El ángulo entre la recta y el plano es
Aquí,
⇒
⇒
⇒
Pregunta 21. Encuentra la ecuación vectorial del plano que pasa por (1, 2, 3) y es perpendicular al plano 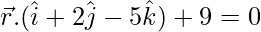 .
.
Solución:
Supongamos que las relaciones de dirección son a, b, c
Dado que la recta pasa por (1, 2, 3), entonces la ecuación de la recta es
….(1)
y la recta es perpendicular al plano
Entonces, la recta es paralela a la normal del plano.
Ahora, las relaciones de dirección son proporcionales a las del plano dado.
⇒ a = λ, b = 2λ, c = -5λ
Ponga estos valores en la ecuación (1), obtenemos
Entonces, la forma vectorial es
es la ecuación requerida.
Pregunta 22. Encuentra el ángulo entre la línea 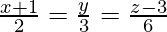 y el plano 10x + 2y – 11z = 3.
y el plano 10x + 2y – 11z = 3.
Solución:
Dado que la ecuación de la recta es
y la ecuación del plano es 10x + 2y – 11z = 3
Asi que,
Como sabemos que el ángulo entre una recta y un plano es
=
⇒ θ = sen −1 (−8/21)
Pregunta 23. Encuentra la ecuación vectorial de la recta que pasa por (1, 2, 3) y es paralela a los planos 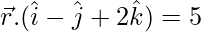 y
y 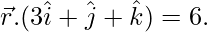
Solución:
Supongamos que ab, b, c son las relaciones de dirección de la línea requerida.
Dado que la recta pasa por (1, 2, 3). Entonces la ecuación de la recta es
…(1)
También dado que eq(1) es paralela a los planos
y
.
Entonces, a – b + 2c = 0 …(2)
3a + b + z = 0 …(3)
Ahora, al resolver las ecuaciones (2) y (3), obtenemos
=> a = -3λ, b = 5λ, c = 4λ
Ahora pon estos valores en la ecuación (1), obtenemos
que es la forma cartesiana de la línea requerida.
Pregunta 24. Encuentra el valor de λ tal que la recta 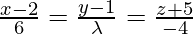 sea perpendicular al plano 3x − y − 2z = 7.
sea perpendicular al plano 3x − y − 2z = 7.
Solución:
Dado que la ecuación de la recta es
y
la ecuación del plano es 3x − y − 2z = 7 y la recta es perpendicular al plano
Entonces, las relaciones de dirección de la línea dada son proporcionales a 6, λ,-4.
y las relaciones de dirección del plano son 3, -1, -2.
Por lo tanto, la línea es paralela al plano dado, la línea es perpendicular
a la normal del plano dado. Asi que,
⇒ (6)(3) + (-1)(-4) + (-2)(11) = 0
⇒ λ = 26
Pregunta 25. Encuentra la ecuación del plano que pasa por los puntos (−1, 2, 0), (2, 2, −1) y paralelo a la recta 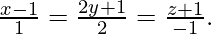
Solución:
La ecuación general del plano que pasa por el punto (−1, 2, 0) es
a(x+1) + b(y-2) + c( z – 0) = 0 ….(1)
Este plano pasa por el punto (2, 2,−1), obtenemos
a(2 + 1) + b(2 – 2) + c( -1 – 0) = 0
⇒ 3a – c = 0 ….(2)
Ahora, a, b, c son la razón de la dirección de la normal al plano (1) y
la normal es perpendicular a la recta, entonces
a + 2b + c = 0 ….(3)
Ahora, al resolver las ecuaciones (2) y (3), obtenemos
a = λ, b = -2 λ, c = 3λ
Ahora ponga todos estos valores en la ecuación (1), obtenemos
λ(x + 1) – 2λ(y – 2) + 3λ(z – 0) = 0
x + 2y + 3z = 3
Por lo tanto, la ecuación del plano requerido es x + 2y + 3z = 3.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA