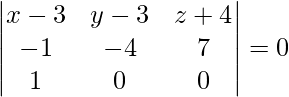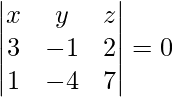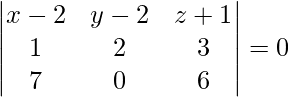Pregunta 1. Encuentra el ángulo entre la recta 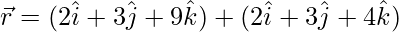 y el plano
y el plano 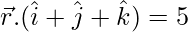 .
.
Solución:
Dado que, la recta es
y el plano es
.
Asi que,
Como sabemos que el ángulo entre una recta y un plano es
Asi que,
⇒
⇒ 9/√87
Pregunta 2. Encuentra el ángulo entre la línea 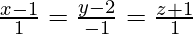 y el plano 2x + y – z = 4.
y el plano 2x + y – z = 4.
Solución:
La línea dada
es paralela al vector
y el plano 2x + y – z = 4 es normal al vector
.
Entonces, el ángulo entre la recta y el plano es
=
= 0
Pregunta 3. Encuentra el ángulo entre la línea que une los puntos (3, -4, -2) y (12, 2, 0) y el plano 3x – y + z = 1.
Solución:
Según la pregunta, la recta pasa por A(3,- 4,- 2) y B(12, 2, 0).
Asi que,
=
=
Entonces, la recta es paralela al vector
y el plano es normal al vector .
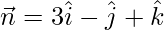
Entonces, el ángulo entre la línea y el plano es,
=
=
Así,
.
Pregunta 4. La recta 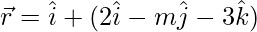 es paralela al plano
es paralela al plano 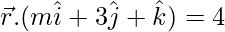 . encuentra m.
. encuentra m.
Solución:
Dar que la ecuación de la línea es
y la ecuación del plano es
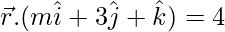
Asi que,
Si una recta es paralela a un plano, entonces la normal al plano es perpendicular a la recta.
⇒
⇒
⇒
⇒ 2m – 3m – 3 = 0
⇒ – metro – 3 = 0
⇒ metro = –3
Pregunta 5. Muestre que la recta cuya ecuación vectorial es 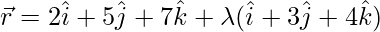 es paralela al plano cuyo vector es
es paralela al plano cuyo vector es 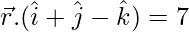 . Además, encuentre la distancia entre ellos.
. Además, encuentre la distancia entre ellos.
Solución:
Dado que el plano pasa por el punto con el vector posición
y es paralelo al vector
.
Entonces, el vector normal
y d = 7 .
= 1 + 3 – 4
= 4 – 4
= 0
Como sabemos que
es perpendicular a
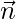
Entonces, la distancia entre la recta y el plano es
= 7/√3 unidades.
Pregunta 6. Encuentra la ecuación vectorial de la línea que pasa por el origen que es perpendicular al plano 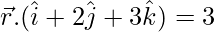 .
.
Solución:
Dado que la recta es perpendicular al plano
Entonces, la recta es paralela a la normal
.
Como sabemos que la ecuación de una recta es pasante
y paralela a
es
⇒
⇒
Pregunta 7. Encuentra la ecuación del plano que pasa por (2, 3, −4) y (1, −1, 3) y es paralelo al eje x.
Solución:
Dado que la ecuación del plano que pasa por el punto (2, 3, -4) es
a(x − 2) + b(y − 3)+c(z + 4) = 0 …(1)
Ya que este plano pasa por el punto (1, -1, 3).
⇒ a(1 − 2) + b( −1 − 3) + c( 3 + 4) = 0
⇒ − a − 4b + 7c = 0 …(2)
La ecuación (1) es paralela al eje x y es perpendicular al plano yz cuya ecuación es x = 0 o 1 . x + 0 . y + 0 . z = 0
⇒ a(1) + b(0) + c(0) = 0 …(3)
Una resolviendo la ecuación (1), (2) y (3), obtenemos
⇒ 7y + 4z – 5 = 0 es la ecuación requerida.
Pregunta 8. Encuentra la ecuación de un plano que pasa por los puntos (0, 0, 0) y (3, −1, 2) y es paralelo a la recta 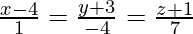
Solución:
Dado que el plano pasa por el punto (0, 0, 0), la ecuación del plano es a(x − 0) + b(y − 0)+c(z + 0) = 0.
⇒ hacha + por + cz = 0 …(1)
y el mismo plano pasa por el punto (3, -1, 2). Entonces, la ecuación del plano es
3a – b + 2c = 0 …(2)
La ecuación (1) es paralela a la línea dada, entonces,
a(1) + b(-4) + c (7) = 0 …(3)
Al resolver las ecuaciones (1), (2) y (3), obtenemos
⇒ x – 19y – 11z = 0
Por lo tanto, la ecuación requerida del plano es x – 19y – 11z = 0
Pregunta 9. Encuentra las ecuaciones vectoriales y cartesianas de la recta que pasa por (1, 2, 3) y es paralela a los planos 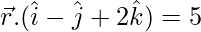 y
y 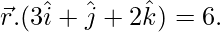
Solución:
Dado que la ecuación de la recta que pasa por (1, 2, 3) es
…(1)
Aquí, la recta dada es paralela al plano x – y + 2z = 5
Entonces, a × 1 + b × – 1 + c × 2 = 0
⇒ a – b + 2c = 0 …(3)
Además, la recta dada es paralela al plano 3x + y + z = 6
Entonces, a × 3 + b × 1 + c × 1 = 0
⇒ 3a + b + c = 0 …(4)
Al resolver la ecuación (3) y (4) obtenemos,
⇒
∴ a = – 3k, b = 5k y c = 4k
Ahora, pon el valor en la ecuación (1), obtenemos
Ahora, multiplicando por k obtenemos
La ecuación requerida es
⇒
Por lo tanto, la ecuación del plano es
Pregunta 10. Demuestra que la recta de sección del plano 5x + 2y – 4z + 2 = 0 y 2x + 8y + 2z – 1 = 0 es paralela al plano 4x – 2y – 5z – 2 = 0.
Solución:
Consideremos a, b y c como las relaciones de dirección.
Asi que,
⇒ a + 4b + c = 0
y, 5a + 2b – 4c = 0
Al resolver las dos ecuaciones anteriores, obtenemos
⇒
Como sabemos que la recta
es paralela al plan a 2 x + b 2 y + c 2 z + d 2 = 0, cuando a 1 a 2 + b 1 b 2 + c 1 c 2 = 0
Entonces, la recta con relación de dirección (a, b, c) es paralela al plano 4x – 2y – 5z – 2 = 0
aa 1 + bb 1 + cc 1 = 0
2(4) + (-1)(-2) + (2)(-5) = 0
Por lo tanto, se demostró que la línea de sección del plano dado es paralela al plano dado.
Pregunta 11. Encuentra la ecuación vectorial de la línea que pasa por el punto (1, -1, 2) y es perpendicular al plano 2x – y + 3z – 5 = 0.
Solución:
Consideremos a, b y c como las relaciones de dirección.
Dado que la ecuación de la recta que pasa por el punto (1, -1, 2)
Asi que,
…..(1)
Además, la recta es paralela a la normal del plano.
⇒
⇒ a = 2λ, b = -λ , c = 3λ
Ahora ponga todos estos valores en la ecuación (1), obtenemos
Entonces, la recta pasa por un punto cuyo vector de posición es
y paralelo a
Asi que,
⇒
es la ecuación requerida.
Pregunta 12. Encuentra la ecuación del plano que pasa por los puntos (2, 2, -1) y (3, 4, 2) y paralelo a la recta cuyas relaciones de dirección son 7, 0, 6.
Solución:
Dado que la ecuación del plano que pasa por el punto (2, 2, -1)
a(x – 2) + b(y – 2) + c(z + 1) = 0 ….(1)
Además, el plano pasa por los puntos (3, 4, 2)
a(3 – 2) + b(4 – 2)+ c(2 + 1) = 0
o, a + 2b + 3c = 0 …(2)
Como sabemos que la recta
es paralela al plan a 2 x + b 2 y + c 2 z + d 2 = 0, cuando a 1 a 2 + b 1 b 2 + c 1 c 2 = 0
De acuerdo con la pregunta, el plano (1) es paralelo a la línea cuyas relaciones de dirección son 7, 0, 6
Entonces, 7a + 0b + 6c = 0 …(3)
Ahora, al resolver la ecuación (1), (2) y (3), tenemos,
⇒ 12x + 15y – 14z – 68 = 0 es la ecuación requerida.
Pregunta 13. Encuentra el ángulo entre la línea 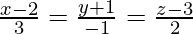 y el plano 3x + 4y + z + 5 = 0.
y el plano 3x + 4y + z + 5 = 0.
Solución:
Dado que la ecuación de la línea es
y la ecuación del plano es 3x + 4y + z + 5 = 0
Asi que,
El ángulo entre una recta y un plano es
⇒
⇒
⇒
De este modo,
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA