Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.12

Pregunta 1(i): Encuentra las coordenadas del punto donde la línea que pasa por (5, 1, 6) y (3, 4, 1) cruza la línea por el plano yz.

Solución:

Sabemos que la ecuación de la recta que pasa por los puntos (x ₁ ,y ₁ ,z ₁ ) y (x ₂ ,y ₂ ,z ₂ ) es $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

Por lo tanto, la ecuación de la línea que une (5, 1, 6) y (3, 4, 1) es $\frac{x-5}{3-5}=\frac{y-1}{4-1}=\frac{z-6}{1-6}$

⇒ $\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}$

Sea, $\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}=\lambda$ , donde $\lambda$ es una constante.

⇒ $x=-2\lambda+5, y=3\lambda+1, z=-5\lambda+6$

Las coordenadas de cualquier punto de la recta tienen la forma de $(-2\lambda+5,3\lambda+1,-5\lambda+6)$

Como la línea cruza el plano yz, el punto $(-2\lambda+5,3\lambda+1,-5\lambda+6)$ debe satisfacer la ecuación del plano x=0,

⇒ $-2\lambda+5=0$ ⇒ $\lambda=\frac{5}{2}$

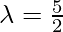
Por tanto, las coordenadas de los puntos viene dada por, poniendo $\lambda=\frac{5}{2}$ obtenemos,

⇒ $(0,\frac{17}{2},\frac{13}{2})$

(ii) Encuentre las coordenadas del punto donde la línea que pasa por (5, 1, 6) y (3, 4, 1) cruza la línea por el plano zx.

Solución:

Sabemos que la ecuación de la recta que pasa por los puntos (x1,y1,z1) y (x2,y2,z2) es $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

Por lo tanto, la ecuación de la línea que une (5, 1, 6) y (3, 4, 1) es $\frac{x-5}{3-5}=\frac{y-1}{4-1}=\frac{z-6}{1-6}$

⇒ $\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}$

Sea, $\frac{x-5}{-2}=\frac{y-1}{3}=\frac{z-6}{-5}=\lambda$ ,donde $\lambda$ es una constante.

⇒ $x=-2\lambda+5, y=3\lambda+1, z=-5\lambda+6$

Las coordenadas de cualquier punto de la recta tienen la forma de $(-2\lambda+5,3\lambda+1,-5\lambda+6)$

Como la línea cruza el plano zx, el punto $(-2\lambda+5,3\lambda+1,-5\lambda+6)$ debe satisfacer la ecuación del plano y=0,

⇒ $3\lambda+1=0$ ⇒ $\lambda=\frac{-1}{3}$

Por tanto, las coordenadas del punto vienen dadas por, poniendo $\lambda=\frac{-1}{3}$ obtenemos,

⇒ $(\frac{17}{3},0,\frac{23}{3})$

Pregunta 2: Encuentra las coordenadas del punto donde la línea que pasa por (3, -4, -5) y (2, -3, 1) cruza el plano 2x+y+z=7.

Solución:

Sabemos que la ecuación de la recta que pasa por los puntos (x1,y1,z1) y (x2,y2,z2) es $\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}=\frac{z-z_1}{z_2-z_1}$

Por tanto, la recta que une los puntos (3, -4, -5) y (2, -3, 1) es $\frac{x-3}{2-3}=\frac{y+4}{-3+4}=\frac{z+5}{1+5}$

⇒ $\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}$

Sea $\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}=\lambda$ donde $\lambda$ es constante.

⇒ $x=-\lambda+3,y=\lambda-4,z=6\lambda-5$

Las coordenadas de cualquier punto de la recta están dadas por $(-\lambda+3,\lambda-4,6\lambda-5)$

La línea cruza el plano, por lo tanto, el punto debe satisfacer la ecuación del plano.

$2(-\lambda+3)+\lambda-4+6\lambda-5=7$

⇒ $\lambda=2$

Por lo tanto, Las coordenadas del punto están dadas por, poniendo $\lambda=2$ ,

⇒ $(-2+3, 2-4, 6(2)-5)$

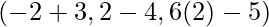
⇒ (1, -2, 7)

Pregunta 3: Encuentra la distancia del punto (-1, -5, -10) desde el punto de intersección de la línea

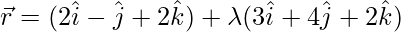$\vec{r}=(2\hat{i}-\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$ y el avion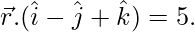 $\vec{r}.(\hat{i}-\hat{j}+\hat{k})=5.$

Solución:

Dada la ecuación de la línea es $\vec{r}=(2\hat{i}-\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$

⇒ $\vec{r}=(2+3\lambda)\hat{i}+(-1+4\lambda)\hat{j}+(2+2\lambda)\hat{k}$

Las coordenadas de cualquier punto de la línea deben tener la forma de $(2+3\lambda,-1+4\lambda,2+2\lambda)$

Sabemos que el punto de intersección de la línea y el plano se encuentra en el plano, usando esto,

⇒ $[(2+3\lambda)\hat{i}+(-1+4\lambda)\hat{j}+(2+2\lambda)\hat{k}].(\hat{i}-\hat{j}+\hat{k})=5.$

⇒ $2+3\lambda+1+4\lambda+2+2\lambda-5=0$

⇒ $\lambda=0$

Por lo tanto, las coordenadas del punto están dadas por, poniendo $\lambda=0$ ,

⇒ (2, -1, 2)

Por lo tanto, ahora la distancia entre (-1, -5, -10) y (2, -1, 2) es,

⇒ $\sqrt{(-1-2)^2+(-5+1)^2+(-10-2)^2}$

⇒ $\sqrt{9+16+144}$ ⇒ 13 unidades

Pregunta 4: Encuentra la distancia del punto (2, 12, 5) desde el punto de intersección de la línea

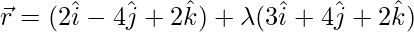$\vec{r}=(2\hat{i}-4\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$ y $\vec{r}.(\hat{i}-2\hat{j}+\hat{k})=0.$

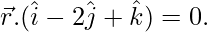
Solución:

Dada la ecuación de la línea es $\vec{r}=(2\hat{i}-4\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$

⇒ $\vec{r}=(2+3\lambda)\hat{i}+(-4+4\lambda)\hat{j}+(2+2\lambda)\hat{k}$

Las coordenadas de cualquier punto de la línea deben tener la forma de $(2+3\lambda,-4+4\lambda,2+2\lambda)$

Sabemos que el punto de intersección de la línea y el plano se encuentra en el plano, usando esto,

⇒ $[(2+3\lambda)\hat{i}+(-4+4\lambda)\hat{j}+(2+2\lambda)\hat{k}].(\hat{i}-2\hat{j}+\hat{k})=0$ .

⇒ $2+3\lambda+8-8\lambda+2+2\lambda=0$

⇒ $\lambda=-4$

Por lo tanto, las coordenadas del punto están dadas por, poniendo $\lambda=-4$ ,

⇒ (14, 12, 10).

Por lo tanto, ahora la distancia entre los puntos (2, 12, 5) y (14, 12, 10) es,

⇒ $\sqrt{(14-2)^2+(12-12)^2+(10-5)^2}$

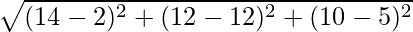
⇒ $\sqrt{144+0+25}$ ⇒ 13 unidades

Pregunta 5: Encuentra la distancia del punto (-1, -5, -10) desde el punto de intersección de la unión A(2, -1, 2) y B(5, 3, 4) con el plano x-y +z=5.

Solución:

La ecuación de la recta que une los puntos A(2, -1, 2) y B(5, 3, 4) es $\frac{x-2}{5-2}=\frac{y-(-1)}{3-(-1)}=\frac{z-2}{4-2}$

⇒ $\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}$

Dejar, $\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}=\lambda$

⇒ $x=3\lambda+2,y=4\lambda-1,z=2\lambda+2$

Las coordenadas de cualquier punto de la recta están dadas por $(3\lambda+2,4\lambda-1,2\lambda+2)$

Sabemos que la intersección de la línea y el plano se encuentra en el plano, entonces,

⇒ $3\lambda+2-(4\lambda-1)+2\lambda+2=5$

⇒ $\lambda=0$

Por lo tanto, las coordenadas de los puntos es, poniendo $\lambda=0$

⇒ (2, -1, 2)

Ahora, la distancia entre los puntos (-1, -5, -10) y (2, -1, 2) es,

⇒ $\sqrt{(2+1)^2+(-1+5)^2+(2+10)^2}$

⇒ $\sqrt{9+16+144}$ ⇒ 13 unidades

Pregunta 6: Encuentra la distancia del punto (3, 4, 4) desde el punto donde la línea que une los puntos A(3, -4, -5) y B(2, -3, 1) interseca el 2x+y +z=7.

Solución:

La ecuación de la recta que pasa por A(3, -4, -5) y B(2, -3, 1) viene dada por $\frac{x-3}{2-3}=\frac{y-(-4)}{-3-(-4)}=\frac{z-(-5)}{1-(-5)}$

⇒ $\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}$

Dejar $\frac{x-3}{-1}=\frac{y+4}{1}=\frac{z+5}{6}=\lambda$

⇒ $x=-\lambda+3,y=\lambda-4,z=6\lambda-5$

Las coordenadas de cualquier punto de la recta están dadas por $(-\lambda+3,\lambda-4,6\lambda-5)$

Sabemos que la intersección de la línea y el plano se encuentra en el plano, entonces,

⇒ $2(-\lambda+3)+(\lambda-4)+(6\lambda-5)=7$

⇒ $5\lambda-3=7$

⇒ $\lambda=2$

Por lo tanto, las coordenadas de los puntos es, poniendo $\lambda=2$

⇒ (1, -2, 7)

Ahora, la distancia entre (3, 4, 4) y (1, -2, 7) es,

⇒ $\sqrt{(3-1)^2+(4+2)^2+(4-7)^2}$

⇒ $\sqrt{4+36+9}$ = 7 unidades

Pregunta 7: Encuentra la distancia del punto (1, -5, 9) desde el plano x- y+ z=5 medido a lo largo de la línea x=y=z.

Solución:

Dado que la ecuación de la línea es x=y=z, también se puede escribir como,

$\frac{x-0}{1}=\frac{y-0}{1}=\frac{z-0}{1}$ , donde (1, 1, 1) son relaciones de dirección de la línea.

Aquí tenemos que medir la distancia a lo largo de la línea, la ecuación de la línea paralela a x=y=z tiene las mismas relaciones de dirección (1, 1, 1),

Entonces, la ecuación de la línea que pasa por (1, -5, 9) y tiene relaciones de dirección (1, 1, 1) es,

⇒ $\frac{x-1}{1}=\frac{y+5}{1}=\frac{z-9}{1}$

Dejar $\frac{x-1}{1}=\frac{y+5}{1}=\frac{z-9}{1}=\lambda$

Las coordenadas de cualquier punto de la recta están dadas por $(\lambda+1,\lambda-5,\lambda+9)$

Sabemos que la intersección de la línea y el plano se encuentra en el plano, entonces,

⇒ $(\lambda+1)-(\lambda-5)+(\lambda+9)=5$

⇒ $\lambda=-10$

Por tanto, las coordenadas del punto vienen dadas por, poniendo $\lambda=-10$ = (-9, -15, -1)

Ahora, la distancia entre los puntos (1, -5, 9) y (-9, -15, -1) es,

⇒ $\sqrt{(1+9)^2+(-5+15)^2+(9+1)^2}$

⇒ $\sqrt{300}$ unidades.

Publicación traducida automáticamente

Artículo escrito por srinivasteja18 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1(i): Encuentra las coordenadas del punto donde la línea que pasa por (5, 1, 6) y (3, 4, 1) cruza la línea por el plano yz.

(ii) Encuentre las coordenadas del punto donde la línea que pasa por (5, 1, 6) y (3, 4, 1) cruza la línea por el plano zx.

Pregunta 2: Encuentra las coordenadas del punto donde la línea que pasa por (3, -4, -5) y (2, -3, 1) cruza el plano 2x+y+z=7.

Pregunta 3: Encuentra la distancia del punto (-1, -5, -10) desde el punto de intersección de la línea

y el avion

Pregunta 4: Encuentra la distancia del punto (2, 12, 5) desde el punto de intersección de la línea

y

Pregunta 5: Encuentra la distancia del punto (-1, -5, -10) desde el punto de intersección de la unión A(2, -1, 2) y B(5, 3, 4) con el plano x-y +z=5.

Pregunta 6: Encuentra la distancia del punto (3, 4, 4) desde el punto donde la línea que une los puntos A(3, -4, -5) y B(2, -3, 1) interseca el 2x+y +z=7.

Pregunta 7: Encuentra la distancia del punto (1, -5, 9) desde el plano x- y+ z=5 medido a lo largo de la línea x=y=z.

Deja una respuesta Cancelar la respuesta

$\vec{r}=(2\hat{i}-\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$ y el avion $\vec{r}.(\hat{i}-\hat{j}+\hat{k})=5.$

$\vec{r}=(2\hat{i}-4\hat{j}+2\hat{k})+\lambda(3\hat{i}+4\hat{j}+2\hat{k})$ y $\vec{r}.(\hat{i}-2\hat{j}+\hat{k})=0.$