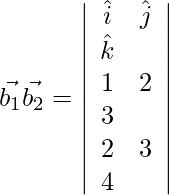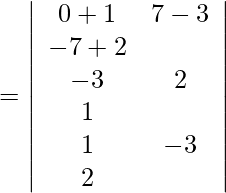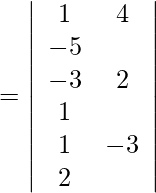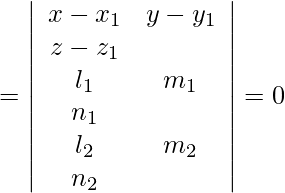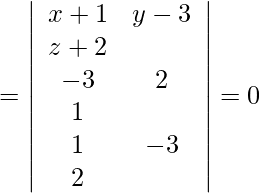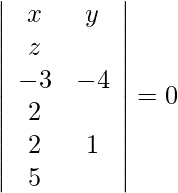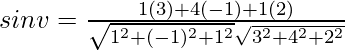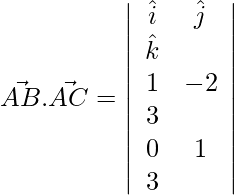Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.13

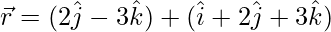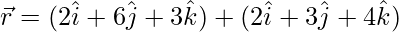Pregunta 1. Demuestra que $\vec{r} = (2\hat{j}-3\hat{k})+λ(\hat{i}+2\hat{j}+3\hat{k})$ y $\vec{r}=(2\hat{i}+6\hat{j}+3\hat{k})+μ(2\hat{i}+3\hat{j}+4\hat{k})$ son coplanares. Además, encuentre la ecuación del plano que los contiene.

Solución:

Sabemos que las rectas $\vec{r} = \vec{a_1}+λ\vec{b_1}$ y $\vec{r} = \vec{a_2}+λ\vec{b_2}$ son coplanares si:

$\vec{a_1}.(\vec{b_1}×\vec{b_2}) = \vec{a_2}.(\vec{b_1}×\vec{b_2})$

$⇒ \vec{b_1}×\vec{b_2}=\left|\begin{array}{cc}\hat{i}&\hat{j}&\hat{k}\\1&2&3\\2&3&4\\\end{array}\right|$

$⇒ \vec{b_1}×\vec{b_2}=-\hat{i}+2\hat{j}-\hat{k}$

$⇒ \vec{a_1}.(\vec{b_1}×\vec{b_2})=(2\hat{j}-3\hat{k}).(-\hat{i}+2\hat{j}-\hat{k})$

$⇒ \vec{a_1}.(\vec{b_1}×\vec{b_2}) = 0 + 4 + 3 = 7$

$⇒ \vec{a_2}.(\vec{b_1}×\vec{b_2})=(2\hat{i}+6\hat{j}+3\hat{k}).(-\hat{i}+2\hat{j}-\hat{k})$

$⇒ \vec{a_2}.(\vec{b_1}×\vec{b_2})=-2+12-3=7$

Como, $\vec{a_1}.(\vec{b_1}×\vec{b_2}) = \vec{a_2}.(\vec{b_1}×\vec{b_2})$ , las rectas son coplanares.

Ecuación del plano que los contiene: $\vec{r}.(\vec{b_1}×\vec{b_2})=\vec{a_1}.(\vec{b_1}×\vec{b_2})$

$⇒ \vec{r}.(-\hat{i}+2\hat{j}-\hat{k}) = 7$

$⇒ \vec{r}.(\hat{i}-2\hat{j}+\hat{k}) = -7$

$⇒ \vec{r}.(\hat{i}-2\hat{j}+\hat{k}) + 7 = 0.$

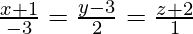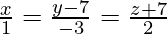Pregunta 2. Demuestra que las rectas $\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z+2}{1}$ y $\frac{x}{1}=\frac{y-7}{-3}=\frac{z+7}{2}$ son coplanares. Además, encuentre la ecuación del plano que los contiene.

Solución:

Conocemos las rectas $\frac{x-x_1}{l_1}=\frac{y-y_1}{m_1}=\frac{z-z_1}{n_1}$ y $\frac{x-x_2}{l_2}=\frac{y-y_2}{m_2}=\frac{z-z_2}{n_2}$ son coplanares si,

$\left|\begin{array}{cc}x_2-x_1&y_2-y_1&z_2-z_1\\l_1&m_1&n_1\\l_2&m_2&n_2\\\end{array}\right|=0$

Asi que, $=\left|\begin{array}{cc}0+1&7-3&-7+2\\-3&2&1\\1&-3&2\\\end{array}\right|$

$= \left|\begin{array}{cc}1&4&-5\\-3&2&1\\1&-3&2\\\end{array}\right|$

= 1(4 + 3) − 4(−6 − 1) − 5(9 − 2)

= 7 + 28 − 35

= 0.

Entonces las rectas son coplanares.

Ecuación del plano: $= \left|\begin{array}{cc}x-x_1&y-y_1&z-z_1\\l_1&m_1&n_1\\l_2&m_2&n_2\\\end{array}\right|=0$

$= \left|\begin{array}{cc}x+1&y-3&z+2\\-3&2&1\\1&-3&2\\\end{array}\right|=0$

⇒ 7x + 7y + 7z = 0.

Pregunta 3. Encuentra la ecuación del plano que contiene la línea 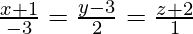$\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z+2}{1}$ y el punto (0,7,-7) y demuestra que la línea 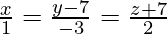$\frac{x}{1}=\frac{y-7}{-3}=\frac{z+7}{2}$ también se encuentra en el mismo plano.

Solución:

Sabemos que la ecuación de un plano que pasa por un punto (x ₁ ,y ₁ ,z ₁ ) está dada por

a(x−x ₁ ) + b(y−y ₁ ) + c(z−z ₁ ) = 0 ……..(1)

Dado que el plano requerido pasa por (0,7,-7), la ecuación se convierte en

hacha + b(y − 7) + c(z + 7) = 0 …….(2)

También contiene $\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z+2}{1}$ y el punto es (−1,3,−2).

a(−1) + b(3 − 7) + c(−2 + 7) = 0

⇒ −a − 4b + 5c = 0

Además, −3a + 2b + c = 0

Resolviendo las ecuaciones, obtenemos x + y + z = 0

Entonces , $\frac{x}{1}=\frac{y-7}{-3}=\frac{z+7}{2}$ se encuentra en el plano x + y + z = 0.

Pregunta 4. Encuentra la ecuación del plano que contiene dos líneas paralelas 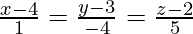$\frac{x-4}{1}=\frac{y-3}{-4}=\frac{z-2}{5}$ y $\frac{x-3}{1}=\frac{y+2}{-4}=\frac{z}{5}.$

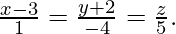
Solución:

Sabemos que la ecuación de un plano que pasa por un punto (x ₁ ,y ₁ ,z ₁ ) está dada por

a(x−x ₁ ) + b(y−y ₁ ) + c(z−z ₁ ) = 0 ……..(1)

El plano requerido pasa por (4,3,2). Por eso,

a(x − 4) + b(y − 3) + c(z − 2) = 0

También pasa por (3,-2,0). Por eso,

a(3 − 4) + b(−2 − 3) + c(0 − 2) = 0

⇒ a + 5b + 2c = 0 …….(2)

Además, a − 4b + 5c = 0 ……..(3)

Resolviendo (2) y (3) por multiplicación cruzada, obtenemos la ecuación del plano como:

⇒ 11x − y − 3z − 35 = 0.

Pregunta 5. Demuestre que las rectas 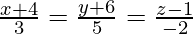$\frac{x+4}{3}=\frac{y+6}{5}=\frac{z-1}{-2}$ y 3x − 2y + 5 = 0 = 2x + 3y + 4z − 4 se intersecan. Encuentra la ecuación del plano.

Solución:

Usando a ₁ a ₂ + b ₁ b ₂ + c ₁ c ₂ = 0, obtenemos

3a − 2b + c = 0 ….(1)

Además, 2a + 3b + 4c = 0. ….(2)

Resolviendo (1) y (2) por multiplicación cruzada, tenemos

$\frac{a}{(-2)(4)-(3)(1)}=\frac{b}{(2)(1)-(3)(4)}=\frac{c}{(3)(3)-(-2)(2)}$

$⇒ \frac{a}{-11}=\frac{b}{-10}=\frac{c}{13}$

Por tanto, la ecuación del plano es 45x − 17y + 25z + 53 = 0

y el punto de intersección es (2,4,−3).

Pregunta 6. Demuestra que el plano cuya ecuación vectorial es 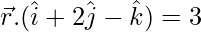$\vec{r}.(\hat{i}+2\hat{j}-\hat{k})=3$ contiene la recta cuya ecuación vectorial es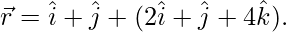 $\vec{r}=\hat{i}+\hat{j}+λ(2\hat{i}+\hat{j}+4\hat{k}).$

Solución:

Aquí, $\vec{b}.\vec{n}=(2\hat{i}+\hat{j}+4\hat{k}).(\hat{i}+2\hat{j}-\hat{k})$

= 2(1) +1(2) + 4(−1)

$⇒ \vec{b}.\vec{n} = 0$

Ahora, $\vec{a}.\vec{n}=(\hat{i}+\hat{j}).(\hat{i}+2\hat{j}-\hat{k})$

= 1(1) + 1(2) + 0(−1)

= 3

$⇒ \vec{a}.\vec{n}=d$

Por lo tanto, la línea dada se encuentra en el plano.

Pregunta 7. Encuentra la ecuación del plano determinada por la intersección de las líneas 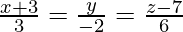$\frac{x+3}{3}=\frac{y}{-2}=\frac{z-7}{6}$ y $\frac{x+6}{1}=\frac{y+5}{-3}=\frac{z-1}{2}.$

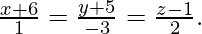
Solución:

Sea el plano ax + by + cz + d = 0

Como el plano pasa por la intersección de las rectas dadas, la normal del plano es perpendicular a las dos rectas.

⇒ 3a − 2b + 6c = 0

y, a − 3b + 2c = 0

Usando la multiplicación cruzada, tenemos

$\frac{a}{-4+18}=\frac{b}{6-6}=\frac{c}{-9+2}$

⇒ $\frac{a}{2}=\frac{b}{0}=\frac{c}{-1}$

Pregunta 8. Encuentra la ecuación vectorial del plano que pasa por los puntos (3,4,2) y (7,0,6) y es perpendicular al plano 2x − 5y − 15 = 0. Además, demuestra que el plano así obtenido contiene la línea 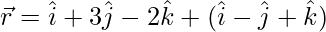$\vec{r}=\hat{i}+3\hat{j}-2\hat{k}+λ(\hat{i}-\hat{j}+\hat{k})$

Solución:

Sea la ecuación del plano $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$

Como el plano pasa por (3,4,2) y (7,0,6), tenemos

$\frac{3}{a}+\frac{4}{b}+\frac{2}{c}=1$ y $\frac{7}{a}+\frac{0}{b}+\frac{6}{c}=1$

Como el plano requerido es perpendicular a 2x − 5y − 15 = 0, tenemos,

$\frac{2}{a}+\frac{(-5)}{b}+\frac{0}{c}=1$

⇒ b = 2.5a

Sustituyendo el valor de b en las ecuaciones anteriores tenemos,

$\frac{3}{a}+\frac{4}{2.5a}+\frac{2}{c}=1$ y $\frac{7}{a}+\frac{6}{c}=1$

Resolviendo las ecuaciones anteriores, tenemos

a = 17/5, b = 17/2 y c = −17/3.

Sustituyendo los valores en la ecuación del plano, obtenemos

5x + 2y − 3z = 17.

La ecuación vectorial del plano se convierte en: $\vec{r}.(5\hat{i}+2\hat{j}-3\hat{k})=17$ .

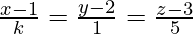Pregunta 9. Si las líneas $\frac{x-1}{-3}=\frac{y-2}{-2k}=\frac{z-3}{2}$ y $\frac{x-1}{k}=\frac{y-2}{1}=\frac{z-3}{5}$ son perpendiculares, encuentra los valores de k y también la ecuación del plano que contiene estas líneas.

Solución:

Las relaciones de dirección de las dos líneas son r ₁ = (−3,−2k,2) y r ₂ = (k,1,5).

Como las rectas son perpendiculares, tenemos

(−3,−2k,2).(k,1,5) = 0

⇒ 3k + 2k − 10 = 0

⇒ 5k = 10

⇒ k = 2

Ahora, la ecuación del plano que contiene las rectas es: $\left|\begin{array}{cc}x&y&z\\-3&-4&2\\2&1&5\\\end{array}\right|=0$

⇒ −22x + 19y + 5z + 31 = 0.

Pregunta 10. Encuentra las coordenadas del punto donde la recta 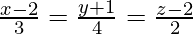$\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}$ interseca al plano x − y + z − 5 = 0. Además, encuentra el ángulo entre la recta y el plano.

Solución:

Cualquier punto en la recta dada tiene la forma (3k + 2, 4k − 1, 2k + 2).

Tenemos, (3k + 2) − (4k − 1) + (2k + 2) − 5 = 0

⇒ k = 0.

Así, las coordenadas del punto se convierten en (2,−1,2).

Sea v el ángulo entre la recta y el plano. Después,

$sinv=\frac{al+bm+cn}{\sqrt{a^2+b^2+c^2}\sqrt{l^2+m^2+n^2}}$

Aquí, l = 3, m = 4, n =2, a =1, b = −1, c = 1.

Por eso, $sinv=\frac{1(3)+4(-1)+1(2)}{\sqrt{1^2+(-1)^2+1^2}\sqrt{3^2+4^2+2^2}}$

⇒ $sinv=\frac{1}{\sqrt{3}\sqrt{29}}$

⇒ $v=sin^{-1}[\frac{1}{\sqrt3\sqrt29}]$

Pregunta 11. Encuentra la ecuación vectorial del plano que pasa por tres puntos con vectores de posición 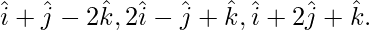$\hat{i}+\hat{j}-2\hat{k},2\hat{i}-\hat{j}+\hat{k},\hat{i}+2\hat{j}+\hat{k}.$

Solución:

Sean A, B y C los tres vectores dados respectivamente.

$\vec{AB}=(2\hat{i}-\hat{j}+\hat{k})-(\hat{i}+\hat{j}-2\hat{k})$

$⇒ \vec{AB}=\hat{i}-2\hat{j}+3\hat{k}$

y, $\vec{AC}=\hat{j}+3\hat{k}$

Ahora, $\vec{AB}.\vec{AC} = \left|\begin{array}{cc}\hat{i}&\hat{j}&\hat{k}\\1&-2&3\\0&1&3\\\end{array}\right|$

⇒ $\vec{n}=-9\hat{i}-3\hat{j}+\hat{k}$

La ecuación del plano es: $\vec{r}.(9\hat{i}+3\hat{j}-\hat{k})=14.$

Las coordenadas de los puntos son (1,1,−2).

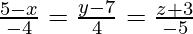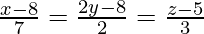Pregunta 12. Demuestra que las rectas $\frac{5-x}{-4}=\frac{y-7}{4}=\frac{z+3}{-5}$ y $\frac{x-8}{7}=\frac{2y-8}{2}=\frac{z-5}{3}$ son coplanares.

Solución:

Conocemos las rectas $\frac{x-x_1}{l_1}=\frac{y-y_1}{m_1}=\frac{z-z_1}{n_1}$ y $\frac{x-x_2}{l_2}=\frac{y-y_2}{m_2}=\frac{z-z_2}{n_2}$ son coplanares si,

$\left|\begin{array}{cc}x_2-x_1&y_2-y_1&z_2-z_1\\l_1&m_1&n_1\\l_2&m_2&n_2\\\end{array}\right|=0$

o, $\left|\begin{array}{cc}8-5&4-7&5+3\\4&4&-5\\7&1&3\\\end{array}\right|$

= $\left|\begin{array}{cc}3&-3&8\\4&4&-5\\7&1&3\\\end{array}\right|$

= 3(12 + 5) + 3(12 + 35) + 8(4 − 28)

= 0.

Por lo tanto, las rectas son coplanares.

Pregunta 13. Encuentra la ecuación del plano que pasa por el punto (3,2,0) y contiene la recta $\frac{x-3}{1}=\frac{y-6}{5}=\frac{z-4}{4}.$

Solución:

La ecuación requerida del plano que pasa por (3,2,0) es:

a(x − 3) + b(y − 2) + cz = 0 ……(1)

Como el avión también pasa por la recta dada, tenemos

4b + 4c = 0 ……(2)

Además, el plano será paralelo entonces,

a + 5b + 4c = 0 ……(3)

Resolviendo (2) y (3), tenemos

$\frac{a}{16-20}=\frac{b}{4-0}=\frac{c}{0-4}=z$

⇒ $-\frac{a}{4}=\frac{b}{4}=-\frac{c}{4}=z$

⇒ a = −z, b = z y c = −z

Poniendo los valores en (1), tenemos

x – y + z – 1 = 0.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Demuestra que y son coplanares. Además, encuentre la ecuación del plano que los contiene.

Pregunta 2. Demuestra que las rectas y son coplanares. Además, encuentre la ecuación del plano que los contiene.

Pregunta 3. Encuentra la ecuación del plano que contiene la línea y el punto (0,7,-7) y demuestra que la línea también se encuentra en el mismo plano.

Pregunta 4. Encuentra la ecuación del plano que contiene dos líneas paralelas y

Pregunta 5. Demuestre que las rectas y 3x − 2y + 5 = 0 = 2x + 3y + 4z − 4 se intersecan. Encuentra la ecuación del plano.

Pregunta 6. Demuestra que el plano cuya ecuación vectorial es contiene la recta cuya ecuación vectorial es

Pregunta 7. Encuentra la ecuación del plano determinada por la intersección de las líneas y

Pregunta 8. Encuentra la ecuación vectorial del plano que pasa por los puntos (3,4,2) y (7,0,6) y es perpendicular al plano 2x − 5y − 15 = 0. Además, demuestra que el plano así obtenido contiene la línea

Pregunta 9. Si las líneas y son perpendiculares, encuentra los valores de k y también la ecuación del plano que contiene estas líneas.

Pregunta 10. Encuentra las coordenadas del punto donde la recta interseca al plano x − y + z − 5 = 0. Además, encuentra el ángulo entre la recta y el plano.

Pregunta 11. Encuentra la ecuación vectorial del plano que pasa por tres puntos con vectores de posición

Pregunta 12. Demuestra que las rectas y son coplanares.

Pregunta 13. Encuentra la ecuación del plano que pasa por el punto (3,2,0) y contiene la recta

Deja una respuesta Cancelar la respuesta

Pregunta 1. Demuestra que $\vec{r} = (2\hat{j}-3\hat{k})+λ(\hat{i}+2\hat{j}+3\hat{k})$ y $\vec{r}=(2\hat{i}+6\hat{j}+3\hat{k})+μ(2\hat{i}+3\hat{j}+4\hat{k})$ son coplanares. Además, encuentre la ecuación del plano que los contiene.

Pregunta 2. Demuestra que las rectas $\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z+2}{1}$ y $\frac{x}{1}=\frac{y-7}{-3}=\frac{z+7}{2}$ son coplanares. Además, encuentre la ecuación del plano que los contiene.

Pregunta 3. Encuentra la ecuación del plano que contiene la línea $\frac{x+1}{-3}=\frac{y-3}{2}=\frac{z+2}{1}$ y el punto (0,7,-7) y demuestra que la línea $\frac{x}{1}=\frac{y-7}{-3}=\frac{z+7}{2}$ también se encuentra en el mismo plano.

Pregunta 4. Encuentra la ecuación del plano que contiene dos líneas paralelas $\frac{x-4}{1}=\frac{y-3}{-4}=\frac{z-2}{5}$ y $\frac{x-3}{1}=\frac{y+2}{-4}=\frac{z}{5}.$

Pregunta 5. Demuestre que las rectas $\frac{x+4}{3}=\frac{y+6}{5}=\frac{z-1}{-2}$ y 3x − 2y + 5 = 0 = 2x + 3y + 4z − 4 se intersecan. Encuentra la ecuación del plano.

Pregunta 6. Demuestra que el plano cuya ecuación vectorial es $\vec{r}.(\hat{i}+2\hat{j}-\hat{k})=3$ contiene la recta cuya ecuación vectorial es $\vec{r}=\hat{i}+\hat{j}+λ(2\hat{i}+\hat{j}+4\hat{k}).$

Pregunta 7. Encuentra la ecuación del plano determinada por la intersección de las líneas $\frac{x+3}{3}=\frac{y}{-2}=\frac{z-7}{6}$ y $\frac{x+6}{1}=\frac{y+5}{-3}=\frac{z-1}{2}.$

Pregunta 8. Encuentra la ecuación vectorial del plano que pasa por los puntos (3,4,2) y (7,0,6) y es perpendicular al plano 2x − 5y − 15 = 0. Además, demuestra que el plano así obtenido contiene la línea $\vec{r}=\hat{i}+3\hat{j}-2\hat{k}+λ(\hat{i}-\hat{j}+\hat{k})$

Pregunta 9. Si las líneas $\frac{x-1}{-3}=\frac{y-2}{-2k}=\frac{z-3}{2}$ y $\frac{x-1}{k}=\frac{y-2}{1}=\frac{z-3}{5}$ son perpendiculares, encuentra los valores de k y también la ecuación del plano que contiene estas líneas.

Pregunta 10. Encuentra las coordenadas del punto donde la recta $\frac{x-2}{3}=\frac{y+1}{4}=\frac{z-2}{2}$ interseca al plano x − y + z − 5 = 0. Además, encuentra el ángulo entre la recta y el plano.

Pregunta 11. Encuentra la ecuación vectorial del plano que pasa por tres puntos con vectores de posición $\hat{i}+\hat{j}-2\hat{k},2\hat{i}-\hat{j}+\hat{k},\hat{i}+2\hat{j}+\hat{k}.$

Pregunta 12. Demuestra que las rectas $\frac{5-x}{-4}=\frac{y-7}{4}=\frac{z+3}{-5}$ y $\frac{x-8}{7}=\frac{2y-8}{2}=\frac{z-5}{3}$ son coplanares.

Pregunta 13. Encuentra la ecuación del plano que pasa por el punto (3,2,0) y contiene la recta $\frac{x-3}{1}=\frac{y-6}{5}=\frac{z-4}{4}.$