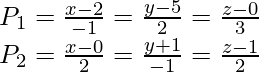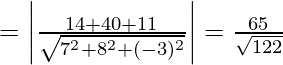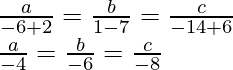Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.14

Pregunta 1. Encuentra la distancia más corta entre las rectas 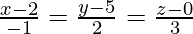$\frac{x-2}{-1}=\frac{y-5}{2}=\frac{z-0}{3}$ y $\frac{x-0}{2}=\frac{y+1}{-1}=\frac{z-1}{2}$ .

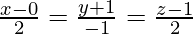Solución:

Dejenos considerar

$P_1=\frac{x-2}{-1}=\frac{y-5}{2}=\frac{z-0}{3}\\ P_2=\frac{x-0}{2}=\frac{y+1}{-1}=\frac{z-1}{2}$

Según las ecuaciones, la línea P ₁ pasa por el punto P(2, 5, 0)

Y la ecuación de un plano que contiene la línea P ₂ es

a(x – 0) + b(y + 1) + c(z – 1) = 0 -(1)

Donde 2a – b + 2c = 0

Si es paralela a la línea P ₁ entonces

-a + 2b + 3c = 0

Asi que,

$\frac{a}{-7}=\frac{b}{-8}=\frac{c}{3}$

Ahora, sustituimos el valor de a, b, c en la ecuación (1) obtenemos

a(x – 0) + b(y + 1) + c(z – 1) = 0

-7(x – 0) – 8(y + 1) + 3(z – 1) = 0

-7x – 8y – 8 + 3z – 3 = 0

7x + 8y – 3z + 11 = 0 -(2)

Entonces, esta es la ecuación del plano que contiene la línea P ₂ y paralelo a la línea P ₁ .

Por lo tanto, la distancia más corta entre P ₁ y P ₂ = Distancia entre el punto P (2, 5, 0) y el plano (2)

$=\left|\frac{14+40+11}{\sqrt{7^2+8^2+(-3)^2}}\right|=\frac{65}{\sqrt{122}}$

Pregunta 2. Encuentra la distancia más corta entre las rectas 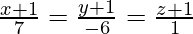$\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ y $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$ .

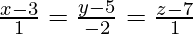Solución:

Dejenos considerar

$P_1:\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$

$P_2:\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$

Supongamos que la ecuación del plano que contiene P ₁ es a(x + 1) + b(y + 1) + c(z+1) = 0

El plano es paralelo a P ₁ = 7a – 6b + c = 0 -(1)

El plano es paralelo a P ₂ = a – 2b + c = 0 -(2)

Al resolver la ecuación (1) y la ecuación (2), obtenemos,

$\frac{a}{-6+2}=\frac{b}{1-7}=\frac{c}{-14+6}\\ \frac{a}{-4}=\frac{b}{-6}=\frac{c}{-8}$

La ecuación del plano es -4(x + 1) – 6(y + 1) – 8(z + 1) = 0

La ecuación final del plano es 4(x + 1) + 6(y + 1) + 8(z + 1) = 0

Pregunta 3. Encuentra la distancia más corta entre las líneas 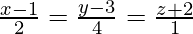$\frac{x-1}{2}=\frac{y-3}{4}=\frac{z+2}{1}$ y 3x – y – 2z + 4 = 0, 2x + y + z + 1 = 0.

Solución:

La ecuación de un plano que contiene la recta 3x – y – 2z + 4 = 0, 2x + y + z + 1 = 0 es

x(2λ + 3) + y(λ – 1) + z(λ – 2) + λ + 4 = 0 -(1)

Si es paralelo a la línea $\frac{x-1}{2}=\frac{y-3}{4}=\frac{z+2}{1}$ entonces,

2(2λ + 3) + 4(λ – 1) + (λ – 2) = 0

λ = 0

Al poner λ = 0 en la ecuación (1) obtenemos,

3x – y – 2z + 4 = 0 -(2)

Como esta ecuación del plano consiste en la segunda recta y paralela a la primera recta.

Es claro que la recta $\frac{x-1}{2}=\frac{y-3}{4}=\frac{z+2}{1}$ pasa por el punto (1, 3, -2)

Entonces, la distancia más corta ‘D’ entre las líneas dadas es igual a la

longitud de la perpendicular desde el punto (1, 3, -2) en el plano (2)

re = $\left|\frac{3-3+4+4}{\sqrt{1+9+4}}\right|=\frac{8}{\sqrt{14}}$

Publicación traducida automáticamente

Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra la distancia más corta entre las rectas y .

Pregunta 2. Encuentra la distancia más corta entre las rectas y .

Pregunta 3. Encuentra la distancia más corta entre las líneas y 3x – y – 2z + 4 = 0, 2x + y + z + 1 = 0.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la distancia más corta entre las rectas $\frac{x-2}{-1}=\frac{y-5}{2}=\frac{z-0}{3}$ y $\frac{x-0}{2}=\frac{y+1}{-1}=\frac{z-1}{2}$ .

Pregunta 2. Encuentra la distancia más corta entre las rectas $\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ y $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$ .

Pregunta 3. Encuentra la distancia más corta entre las líneas $\frac{x-1}{2}=\frac{y-3}{4}=\frac{z+2}{1}$ y 3x – y – 2z + 4 = 0, 2x + y + z + 1 = 0.