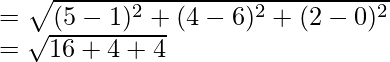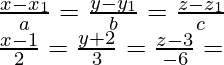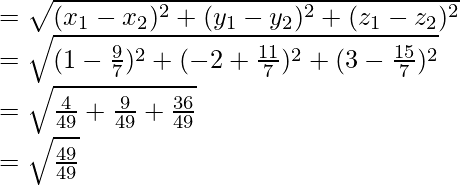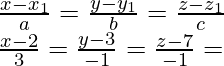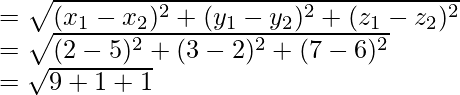Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.15

Pregunta 1. Encuentra la imagen del punto (0, 0, 0) en el plano 3x + 4y – 6z + 1 = 0.

Solución:

De acuerdo con la pregunta que tenemos

Plano = 3x + 4y – 6z + 1 = 0

La recta que pasa por el origen y es perpendicular al plano está dada por

$\frac{x}{3}=\frac{y}{4}=\frac{z}{-6}=r$

Entonces, sea la imagen de (0, 0, 0) = (3r, 4r, -6r)

El punto medio de (0, 0, 0) y (3r, 4r, -6r) se encuentra en el plano dado

3(3r/2) + 2(4r) – 3(-6y) + 1 = 0

30,5 años = -1

r = -2/61

Entonces, la imagen es (-6/61, -8/61, 12/61)

Pregunta 2. Encuentra el reflejo del punto (1, 2, -1) en el plano 3x – 5y + 4z = 5

Solución:

Según la pregunta tenemos que encontrar el reflejo de

el punto P(1, 2, -1) en el plano 3x – 5y + 4z = 5

Entonces, sea Q = reflejo del punto P

R = punto medio de PQ.

Entonces, R se encuentra en el plano 3x – 5y + 4z = 5.

Ahora, las relaciones de dirección de PQ son proporcionales a 3, -5, 4 y

PQ está pasando por (1, 2, -1).

Entonces, la ecuación de PQ es,

$\frac{x-1}{3}=\frac{y-2}{-5}=\frac{z+1}{4}=λ$

Sea Q (3)

Las coordenadas de R son = $\left(\frac{3λ+1+1}{2},\frac{-5λ+2+2}{2},\frac{4λ-1-1}{2}\right)=\left(\frac{3λ+2}{2},\frac{-5λ+4}{2},\frac{4λ-2}{2}\right)$

Dado que R se encuentra en el plano dado, es decir, 3x – 5y + 4z = 5

Por lo tanto, $3\left(\frac{3λ+2}{2}\right)-5\left(-\frac{5λ+4}{2}\right)+4\left(\frac{4λ-2}{2}\right)=5$

9

= ((48/25)+1, (-16/5)+2, (64/25)-1)

= (73/25, -6/5, 39/25)

Por lo tanto, la reflexión del punto (1, 2, -1) = (73/25, -6/5, 39/25)

Pregunta 3. Halla las coordenadas del pie de la perpendicular trazada desde el punto (5, 4, 2) hasta la recta 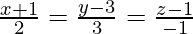$\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}$ . De aquí o de lo contrario deducir la longitud de la perpendicular.

Solución:

Según la pregunta tenemos que encontrar el pie de la perpendicular, digamos Q,

trazada desde el punto P(5, 4, 2) hasta la línea $\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}=λ$

Entonces, supongamos Q = (2) -Ecuación (1)

Relación de dirección de la línea PQ son = (2)

Aquí, la línea PQ es perpendicular a la línea dada AB

Asi que,

un ₁ un ₂ + segundo ₁ segundo ₂ + do ₁ do ₂ = 0

(2)(2) + (3)(3) + (-)(-1) = 0

4

fórmula de distancia

$= \sqrt{(5-1)^2+(4-6)^2+(2-0)^2}\\ = \sqrt{16+4+4}\\$

= √24

= 2√6

Entonces, el pie de la perpendicular es (1, 6, 0)

La longitud de la perpendicular es 2√6 unidades.

Pregunta 4. Encuentra la imagen del punto con vector de posición 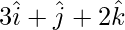$3\hat{i}+\hat{j}+2\hat{k}$ en el plano 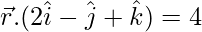$\vec{r}.(2\hat{i}-\hat{j}+\hat{k})=4$ . Halla también el vector de posición del pie de la perpendicular y la ecuación de la recta perpendicular que pasa por $3\hat{i}+\hat{j}+2\hat{k}$ .

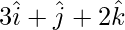Solución:

De acuerdo a la pregunta tenemos que encontrar la imagen del punto P(3, 1, 2)

en el plano $\vec{r}.(2\hat{i}-\hat{j}+\hat{k})=4$ o 2x – y + z = 4.

Sea Q la imagen del punto P.

Asi que,

Las relaciones de dirección de la normal al punto = 2, -1, 1

Las relaciones de dirección de la línea PQ perpendicular a 2, -1, 1 y

PQ está pasando por (3, 1, 2)

Entonces la ecuación de PQ es

$\frac{x-3}{2}=\frac{y-1}{-1}=\frac{z-2}{1}=λ$

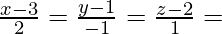
El punto general sobre la recta PQ es = (2

(2

$\left(\frac{2λ+3+3}{2},\frac{-λ+1+1}{2},\frac{λ+2+2}{2}\right)=\left(\frac{2λ+6}{2},\frac{-λ+2}{2},\frac{λ+4}{2}\right)$

Como R se encuentra en el plano 2x – y + z = 4, obtenemos

$2\left(\frac{2λ+6}{2}\right)-\left(\frac{-λ+2}{2}\right)+\left(\frac{λ+4}{2}\right)=4$

4

Imagen de P = Q(2 (-1) + 3, – (-1) + 1, -1 + 2)

Imagen de P = (1, 2, 1)

La ecuación de la recta perpendicular que pasa por $3\hat{i}+\hat{j}+2\hat{k}$ es

$\vec{r}=3\hat{i}+\hat{j}+2\hat{k}+λ(2\hat{i}-\hat{j}+\hat{k})$

El vector de posición del punto de la imagen es

$3\hat{i}+\hat{j}+2\hat{k}+λ(2\hat{i}-\hat{j}+\hat{k})=(3+2λ)\hat{i}+(1-λ)\hat{j}+(2+k)\hat{k}$

El vector de posición del pie de la perpendicular es

$\frac{[(3+2λ)\hat{i}+(1-λ)\hat{j}+(2+k)\hat{k}]+[3\hat{i}+\hat{j}+2\hat{k}]}{2}$

$=(3+λ)\hat{i}+(1-\frac{λ}{2})\hat{j}+(2+\frac{λ}{2})\hat{k}$

Poniendo

$2\hat{i}+\frac{3}{2}\hat{j}+\frac{3}{2}\hat{k}$

Pregunta 5. Encuentra las coordenadas del pie de la perpendicular desde el punto (1, 1, 2) al plano 2x – 2y + 4z + 5 = 0. Además, encuentra la longitud de la perpendicular.

Solución:

Según la pregunta que tenemos,

Plano = 2x – 2y + 4z + 5 = 0 -Ecuación(1)

Punto = (1, 1, 2)

y encuentra las coordenadas del pie de la perpendicular

$= \left|\frac{2-2+8+5}{\sqrt{1+1+4}}\right|=\frac{13}{\sqrt{6}}$

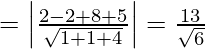
Supongamos que el pie de la perpendicular = (x, y, z).

Entonces, los DR son proporcionales

$\frac{x-1}{2}=\frac{y-1}{-2}=\frac{z-2}{4}=k$

x = 2k + 1

y = -2k + 1

z = 4k + 2

Sustituye (x, y, z) = (2k + 1, -2k + 1, 4k + 2) en la ecuación (1), obtenemos

2x – 2y + 4z + 5 = 0

4k + 2 + 4k – 2 + 16k + 8 + 5 = 0

24k = -13

k = -13/24

Entonces, las coordenadas del pie de la perpendicular (x, y, z) = (-1/12, 5/3, -1/6)

Pregunta 6. Encuentra la distancia del punto (1, -2, 3) desde el plano x – y + z + 5 medido a lo largo de una línea paralela a 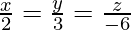$\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}$

Solución:

De acuerdo con la pregunta, tenemos que encontrar la distancia del punto P(1, -2, 3)

desde el plano x – y + z = 5 medido

paralela a la línea AB, $\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}$

Supongamos Q = Punto medio de la recta que une P con el plano.

Tenemos, PQ paralela a la línea AB

Por lo tanto, la ecuación de PQ es,

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\\ \frac{x-1}{2}=\frac{y+2}{3}=\frac{z-3}{-6}=λ\\$

El punto general sobre la recta PQ = (2)

Supongamos que las coordenadas de Q = (2)

Por lo tanto, Q se encuentra en el plano x – y + z = 5

(2) – (3) + (-6) = 5

2

Coordenada de Q = (2, 3, -6) -Ecuación(1)

Ahora, encontramos la distancia entre (1, -2, 3) y el plano = PQ

$=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}\\ =\sqrt{(1-\frac{9}{7})^2+(-2+\frac{11}{7})^2+(3-\frac{15}{7})^2}\\ =\sqrt{\frac{4}{49}+\frac{9}{49}+\frac{36}{49}}\\ =\sqrt{\frac{49}{49}}$

= 1

Por lo tanto, la distancia requerida es 1 unidad.

Pregunta 7. Encuentra las coordenadas del pie la perpendicular desde el punto (2, 3, 7) al plano 3x – y – z = 7. Además, encuentra la longitud de la perpendicular.

Solución:

Supongamos que Q sea el pie de la perpendicular.

Ahora, las relaciones de dirección del plano normal son 3, -1, -1

$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}\\ \frac{x-2}{3}=\frac{y-3}{-1}=\frac{z-7}{-1}=λ$

El punto general en la línea PQ

= (3

El punto Q se encuentra en el plano 3x – y – z = 7

De este modo,

3(3) – (-) – (-) = 7

9

Q = (3(1) + 2, -(1) + 3, -(1) + 7)

P = (5, 2, 6)

Encuentre la longitud de la perpendicular PQ

$=\sqrt{(x_1-x_2)^2 + (y_1-y_2)^2 + (z_1-z_2)^2}\\ =\sqrt{(2-5)^2+(3-2)^2+(7-6)^2}\\ =\sqrt{9+1+1}\\$

= √11

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.15 | Serie 1

Pregunta 1. Encuentra la imagen del punto (0, 0, 0) en el plano 3x + 4y – 6z + 1 = 0.

Pregunta 2. Encuentra el reflejo del punto (1, 2, -1) en el plano 3x – 5y + 4z = 5

Pregunta 3. Halla las coordenadas del pie de la perpendicular trazada desde el punto (5, 4, 2) hasta la recta $\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}$ . De aquí o de lo contrario deducir la longitud de la perpendicular.

Pregunta 4. Encuentra la imagen del punto con vector de posición $3\hat{i}+\hat{j}+2\hat{k}$ en el plano $\vec{r}.(2\hat{i}-\hat{j}+\hat{k})=4$ . Halla también el vector de posición del pie de la perpendicular y la ecuación de la recta perpendicular que pasa por $3\hat{i}+\hat{j}+2\hat{k}$ .

Pregunta 5. Encuentra las coordenadas del pie de la perpendicular desde el punto (1, 1, 2) al plano 2x – 2y + 4z + 5 = 0. Además, encuentra la longitud de la perpendicular.

Pregunta 6. Encuentra la distancia del punto (1, -2, 3) desde el plano x – y + z + 5 medido a lo largo de una línea paralela a $\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}$

Pregunta 7. Encuentra las coordenadas del pie la perpendicular desde el punto (2, 3, 7) al plano 3x – y – z = 7. Además, encuentra la longitud de la perpendicular.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la imagen del punto (0, 0, 0) en el plano 3x + 4y – 6z + 1 = 0.

Pregunta 2. Encuentra el reflejo del punto (1, 2, -1) en el plano 3x – 5y + 4z = 5

Pregunta 3. Halla las coordenadas del pie de la perpendicular trazada desde el punto (5, 4, 2) hasta la recta . De aquí o de lo contrario deducir la longitud de la perpendicular.

Pregunta 4. Encuentra la imagen del punto con vector de posición en el plano . Halla también el vector de posición del pie de la perpendicular y la ecuación de la recta perpendicular que pasa por .

Pregunta 5. Encuentra las coordenadas del pie de la perpendicular desde el punto (1, 1, 2) al plano 2x – 2y + 4z + 5 = 0. Además, encuentra la longitud de la perpendicular.

Pregunta 6. Encuentra la distancia del punto (1, -2, 3) desde el plano x – y + z + 5 medido a lo largo de una línea paralela a

Pregunta 7. Encuentra las coordenadas del pie la perpendicular desde el punto (2, 3, 7) al plano 3x – y – z = 7. Además, encuentra la longitud de la perpendicular.

Deja una respuesta Cancelar la respuesta

Pregunta 3. Halla las coordenadas del pie de la perpendicular trazada desde el punto (5, 4, 2) hasta la recta $\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}$ . De aquí o de lo contrario deducir la longitud de la perpendicular.

Pregunta 4. Encuentra la imagen del punto con vector de posición $3\hat{i}+\hat{j}+2\hat{k}$ en el plano $\vec{r}.(2\hat{i}-\hat{j}+\hat{k})=4$ . Halla también el vector de posición del pie de la perpendicular y la ecuación de la recta perpendicular que pasa por $3\hat{i}+\hat{j}+2\hat{k}$ .

Pregunta 6. Encuentra la distancia del punto (1, -2, 3) desde el plano x – y + z + 5 medido a lo largo de una línea paralela a $\frac{x}{2}=\frac{y}{3}=\frac{z}{-6}$