Pregunta 11. Un plano pasa por el punto (1, -2, 5) y es perpendicular a la línea que une el origen con el punto ( 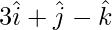 ). Encuentra las formas vectorial y cartesiana de la ecuación del plano.
). Encuentra las formas vectorial y cartesiana de la ecuación del plano.
Solución:
Como sabemos que la ecuación vectorial de un plano que pasa por un punto
y es normal a
es
….(i)
Aquí,
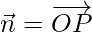
= Vector de posición de P – Posición del vector de O
=
Ahora, pon todos estos valores en la ecuación (i), obtenemos,
….(2)
Ahora pon
en la ecuación (2), obtenemos
(x)(3) + (y)(1) + (z)(−1) = -4
3x + y − z = -4
Entonces, esta es la ecuación requerida del plano.
Pregunta 12. Encuentra la ecuación del plano que biseca el segmento de recta que une los puntos (1, 2, 3) y (3, 4, 5) y forma ángulo recto con él.
Solución:
Como sabemos que la ecuación vectorial de un plano que pasa por un punto
y es normal a
es
…..(i)
Aquí,
= punto medio de AB
Asi que,

= Posición del vector de A + Posición del vector de B/ 2
=
=
Y,
= Posición del vector de B – Posición del vector de A
=
=
Ahora ponga todos estos valores en la ecuación (1), obtenemos
…..(2)
Ahora pon
en la ecuación (2), obtenemos
(x)(2) + (y)(2) + (z)(2) = 18
2x + 2y + 2z = 18
o podemos escribir como
x + y + z = 9
Entonces, esta es la ecuación requerida del plano.
Pregunta 13. Muestre que las normales a los siguientes pares de planos son perpendiculares entre sí:
(i) x – y + z – 2 = 0 y 3x + 2y – z + 4 = 0
Solución:
Dadas las ecuaciones de los planos son
x – y + z – 2 = 0 y 3x + 2y – z + 4 = 0
Primero resolvemos, x – y + z – 2 = 0
…..(i)
Ahora resolvemos, 3x + 2y – z =- 4
…(ii)
Entonces, de las ecuaciones (i) y (ii), concluimos que
es normal a la ecuación (i) y
es normal a la ecuación (ii)
Asi que,
=
= (1)(3) + (-1)(2) + (1)(-1)
=3 – 2 – 1
= 3 – 3 = 0
Por lo tanto,
es perpendicular a
(ii) 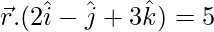 y
y 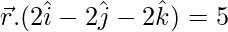
Solución:
Dadas las ecuaciones de los planos son
y
Así que primero resolvemos,
…..(1)
Ahora resolvemos,
……(2)
Entonces, de las ecuaciones (i) y (ii), concluimos que
es normal a la ecuación (i) y
es normal a la ecuación (ii)
Asi que,
=
= (2)(2) + (-1)(-2) + (3)(-2)
= 4 + 2 – 6
= 6 – 6
= 0
Por lo tanto,
es perpendicular a
Pregunta 14. Demostrar que el vector normal al plano 2x + 2y + 2z = 3 tiene la misma inclinación que los ejes coordenados.
Solución:
Ecuación del plano = 2x + 2y + 2z = 3
Asi que,
Entonces, la normal al avión.
y la relación de dirección de
Entonces, el coseno director de
….(1)
= √[(2) 2 + (2) 2 + (2) 2 ]
= √[4 + 4 + 4]
= √12 = 2√3
Ahora pon el valor de |\vec{n}| en la ecuación (1), obtenemos
Coseno director de |\vec{n}| =
=
Entonces, u = 1/√3, v = 1/√3, W = 1/√3
Supongamos que α, β, γ es el ángulo que forma la normal \vec{n} con los ejes coordenados.
Entonces, u = cos α = 1/√3
α = cos -1 1/√3 ….(2)
v = cos β = 1/√3
β = cos -1 1/√3 ….(3)
w = cos γ = 1/√3
γ = cos -1 1/√3 ….(4)
Entonces, de la ecuación (2), (3) y (4), obtenemos
α = β = γ
Por tanto, se demostró que el vector normal al plano 2x + 2y + 2z = 3 tiene la misma inclinación que los ejes coordenados.
Pregunta 15. Encuentra un vector de magnitud 26 unidades normal al plano 12x – 3y + 4y = 1.
Solución:
Dado que,
La ecuación del plano es = 12x – 3y + 4y = 1
y la magnitud = 26 unidades
Asi que,
La normal al plano es
= √[(12) 2 + (-3) 2 + (4) 2 ]
= √[144 + 9 + 16]
= √169 = 13
Por lo tanto, el vector unitario
=
Ahora encontramos un vector normal al plano con magnitud
Asi que,
26 = 26
= 26
=
Entonces, este es el vector requerido
Pregunta 16. Si la línea trazada desde (4, -1, 2) se encuentra con un plano en ángulo recto en el punto (-10, 5, 4), encuentra la ecuación del plano.
Solución:
Como sabemos que la ecuación vectorial de un plano que pasa por un punto
y es normal a
es
…..(i)
Aquí,
= vector de posición de B
Asi que,
y
= Posición del vector de B – Posición del vector de A
=
=
Ahora ponga todos estos valores en la ecuación (1), obtenemos
![Rendered by QuickLaTeX.com \vec{r}(-14\hat{i}+6\hat{j}+2\hat{k})-[(-10)(-14)+(5)(6)+(4)(2)]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9866b7149afdf3f18bceade6c24c8cae_l3.png)
…..(2)
Ahora pon
en la ecuación (2), obtenemos
(x)(-14) + (y)(6) + (z)(2) = 178
-14x + 6y + 3z = 178
O podemos escribir como
7x – 2y – z = -89
Entonces, esta es la ecuación requerida del plano.
Pregunta 17. Encuentra la ecuación del plano que biseca el segmento de recta que une los puntos (-1, 2, 3) y (3, -5, 6) en ángulo recto.
Solución:
Supongamos que el punto (-1, 2, 3) es el punto A y el punto (3, -5, 6) es el punto B y C es el punto medio de la línea del segmento de línea AB
Como sabemos que la ecuación vectorial de un plano que pasa por un punto
y es normal a
es
…(i)
Aquí,
= vector de posición de C
Entonces,
[Porque c es el punto medio de la línea AB]
Ahora,
= Vector de posición de B- Vector de posición de A
=
=
=
Ahora ponga todos estos valores en la ecuación (1), obtenemos
= 28 ….(2)
Ahora pon
en la ecuación (2), obtenemos
(x)(4) + (y)(-7) + (z)(3) = 28
4x – 7y + 3z = 28
Entonces, esta es la ecuación requerida del plano.
Pregunta 18. Encuentra las ecuaciones vectoriales y cartesianas del plano que pasa por el punto (5, 2, -4) y es perpendicular a la recta con relaciones de dirección 2, 3, -1.
Solución:
De acuerdo a la pregunta dada
Como sabemos que la ecuación vectorial de un plano que pasa por un punto
y es normal a
es
Asi que,
….(1)
Para ecuación cartesiana:
Ponga
en la ecuación (1), obtenemos
(x)(2) + (y)(3) + (z)(-1) = 20
2x + 3y -z = 20
Entonces, esta es la ecuación requerida del plano.
Pregunta 19. Si O es el origen y las coordenadas de P son (1, 2, -3), entonces encuentra la ecuación del plano que pasa por P y es perpendicular a OP.
Solución:
Según la pregunta, un paso normal por el punto O(0, 0, 0) y P (1, 2, -3)
Asi que,
y
Como sabemos que la ecuación vectorial de un plano que pasa por un punto
y es normal a
es
Asi que,
Para ecuación cartesiana:
Ponga
en la ecuación (1), obtenemos
(x)(1) + (y)(2) + (z)(-3) = 14
x + 2y – 3z = 14
Entonces, esta es la ecuación requerida del plano.
Pregunta 20. Si O es el origen y las coordenadas de A son (a, b, c). Encuentre los cosenos directores de OA y la ecuación del plano que pasa por A en ángulo recto con OA.
Solución:
De acuerdo a la pregunta se da que, O es el origen y las coordenadas de A son (a, b, c)
Asi que,
Dado que las relaciones de dirección de OA son proporcionales a a, b, c
Entonces, los cosenos directores son:
Entonces la ecuación de la recta es,
hacha + por + cz = a 2 + b 2 + c 2
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA