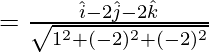Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.4

Pregunta 1. Encuentra la ecuación vectorial de un plano que está a una distancia de 3 unidades del origen y tiene $\hat{k}$ como vector unitario normal a él.

Solución:

Sabemos que la ecuación vectorial de un plano normal al vector unitario $\hat{n}$ y a una distancia d del origen se da como

$\vec{r}.\hat{n} = d$

Aquí, d = 3 unidades, obtenemos

$\vec{r}.\hat{k} = 3$

Pregunta 2. Encuentra la ecuación vectorial de un plano que está a una distancia de 5 unidades del origen y que es normal al vector $\hat{i} - 2\hat{j} - 2\hat{k}.$

Solución:

Sabemos que la ecuación vectorial de un plano normal al vector unitario $\hat{n}$ y a una distancia d del origen se da como

$\vec{r}.\hat{n} = d$

Aquí, d = 5 unidades

y $\vec{n} = \hat{i} - 2\hat{j} - 2\hat{k}.$

$\hat{n} = \frac{\vec{n}}{\vec{|n|}}$

$= \frac{\hat{i} - 2\hat{j} - 2\hat{k}}{\sqrt{1^2 + (-2)^2 + (-2)^2}}$

$= \frac{\hat{i} - 2\hat{j} - 2\hat{k}}{\sqrt{9}}$

$= \frac{\hat{i} - 2\hat{j} - 2\hat{k}}{3}$

Por lo tanto, la ecuación requerida es,

$\vec{r}.\frac{1}{3}(\hat{i} - 2\hat{j} - 2\hat{k}) = 5$

Pregunta 3. Reduzca la ecuación 2x – 3y – 6z = 14 a la forma normal y, por lo tanto, encuentre la longitud de la perpendicular desde el origen hasta el plano. Además, encuentre la dirección de los cosenos de la normal al plano.

Solución:

$(x\hat{i} + y\hat{j} + z\hat{k}).(2\hat{i} - 3\hat{j} - 6\hat{k}) = 14$

Dividiendo la ecuación por $\sqrt{2^2 + (- 3)^2 + (- 6)^2}$

$\vec{r}.\frac{(2\hat{i}- 3\hat{j} - 6\hat{k})}{\sqrt{4 + 9 + 36}} = \frac{14}{\sqrt{4 + 9 + 36}}$

$⇒ \vec{r}.[\frac{2}{7}\hat{i} - \frac{3}{7}\hat{j} - \frac{6}{7}\hat{k}] = 2$ ……(1)

Dado que la ecuación vectorial de un plano de distancia d y normal al vector unitario n viene dada por

$\vec{r}.\hat{n} = d$ ……(2)

Comparando (1) y (2), obtenemos

Distancia desde el origen = 2 unidades

Coseno director de la normal al plano = $\frac{2}{7}, - \frac{3}{7}, \frac{6}{7}$

Pregunta 4. Reduzca la ecuación $\vec{r}.(\hat{i} - 2\hat{j} + 2\hat{k}) + 6 = 0$ a la forma normal y, por lo tanto, encuentre la longitud de la perpendicular desde el origen hasta el plano.

Solución:

$Given: \vec{r}.(\hat{i} - 2\hat{j} + 2\hat{k}) = -6$

Multiplicando ambos lados por -1, obtenemos

$\vec{r}.(\hat{-i} + 2\hat{j} - 2\hat{k}) = 6$

$⇒ \vec{r}.\vec{n} = 6$ …..(1)

$|\vec{n}| = \sqrt{(-1)^2 + 2^2 + (-2)^2} = 3$

Dividiendo (1) por 3 en ambos lados,

$\vec{r}.[-\frac{\hat{i}}{3} + \frac{2}{3}\hat{j} - \frac{2}{3}\hat{k}] = 2$

Dado que la ecuación vectorial de un plano de distancia d y normal al vector unitario n viene dada por

$\vec{r}.\hat{n} = d$ ……(2)

Comparando (1) y (2), obtenemos

re = 2

$\hat{n} = [-\frac{\hat{i}}{3} + \frac{2}{3}\hat{j} - \frac{2}{3}\hat{k}]$

Longitud de lo normal = 2 unidades.

Pregunta 5. Escribe la forma normal de la ecuación 2x – 3y + 6z + 14 = 0.

Solución:

$(x\hat{i} + y\hat{j} + z\hat{k}).(2\hat{i} - 3\hat{j} + 6\hat{k}) = -14$

$⇒ \hat{r}.(2\hat{i} - 3\hat{j} + 6\hat{k}) = -14$

Multiplicando ambos lados por -1, obtenemos

$\vec{r}.(-2\hat{i} + 3\hat{j} - 6\hat{k}) = 14$

$⇒ \vec{r}.\vec{n} = 14$ …..(1)

$|\vec{n}| = \sqrt{(-2)^2 + 3^2 + (-6)^2} = 7$

Dividiendo (1) por 7 en ambos lados,

$\vec{r}.[-\frac{2}{3}\hat{i} + \frac{3}{7}\hat{j} - \frac{6}{7}\hat{k}] = 2$

Por lo tanto, la forma normal de la ecuación es

$-\frac{2}{7}x + \frac{3}{7}y - \frac{6}{7}z = 2$

Pregunta 6. Las relaciones de dirección de la perpendicular desde el origen a un plano son 12, -3, 4 y la longitud de la perpendicular es 5. Encuentra la ecuación del plano.

Solución:

vectores normales = $\vec{n} = 12\hat{i} - 3\hat{j} + 4\hat{k}$

$|\vec{n}| = \sqrt{(12)^2 + (-3)^2 + (4)^2} = \sqrt{169} = 13$

Entonces, vector unitario normal $= \hat{n} = \frac{\vec{n}}{ |\vec{n}|}$

$= \frac{12}{13}\hat{i} - \frac{3}{13}\hat{j} + \frac{4}{13}\hat{k} = 5$

Dado que la ecuación vectorial de un plano de distancia d y normal al vector unitario n viene dada por

$\vec{r}.\hat{n} = d$

$⇒ \vec{r}.[\frac{12}{13}\hat{i} - \frac{3}{13}\hat{j} + \frac{4}{13}\hat{k}] = 5$

o, $\frac{12}{13}x - \frac{3}{13}y + \frac{4}{13}z = 5$

Pregunta 7. Encuentra el vector unitario normal al plano x + 2y + 3z – 6 = 0.

Solución:

$(x\hat{i} + y\hat{j} + z\hat{k}).(\hat{i} + 2\hat{j} + 3\hat{k}) = 6$

$⇒ \hat{r}.(\hat{i} + 2\hat{j} + 3\hat{k}) = 6$

$⇒ \vec{r}.\vec{n} = 6$ …….(1)

$|\vec{n}| = \sqrt{(1)^2 + 2^2 + (3)^2} = \sqrt{14}$

Dividiendo (1) por $\sqrt{14}$ , obtenemos

$\vec{r}.[\frac{1}{\sqrt14}\hat{i} + \frac{2}{\sqrt14}\hat{j} + \frac{3}{\sqrt14}\hat{k}] = \frac{6}{\sqrt14}$

Dado que la ecuación vectorial de un plano de distancia d y normal al vector unitario n viene dada por

$\vec{r}.\hat{n} = d$ …..(2)

Por lo tanto, vector unitario normal = $\hat{n} = \frac{1}{\sqrt14}\hat{i} + \frac{2}{\sqrt14}\hat{j} + \frac{3}{\sqrt14}\hat{k}$

Pregunta 8. Encuentra la ecuación de un plano que está a una distancia de 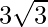$3\sqrt{3}$ unidades del origen y la normal a la que está igualmente inclinada con los ejes de coordenadas.

Solución:

Dado que la ecuación vectorial de un plano de distancia d y normal al vector unitario n viene dada por

$\vec{r}.\hat{n} = d$

re = $3\sqrt{3} units$

Sea $\vec{a}$ un vector normal, $\vec{a} = p\hat{i} + q\hat{j} + r\hat{k}$

Como $\vec{a}$ está igualmente inclinado a los ejes de coordenadas, sean l, m, n los cosenos de $\vec{n}$ . También l = m = n.

Sabemos, l ² + m ² + n ² = 1

o, $l = m = n = \frac{1}{\sqrt{3}}$

Ahora, $\hat{a} = \frac{\hat{i}}{\sqrt{3}} + \frac{\hat{j}}{\sqrt{3}} + \frac{\hat{k}}{\sqrt{3}}$

La ecuación vectorial del plano requerido es

$\vec{r}.\frac{1}{\sqrt3}[\hat{i} + \hat{j} + \hat{k}] = 3\sqrt{3}$

o, $\vec{r}(\hat{i} + \hat{j} + \hat{k}) = 9$

o, x + y + z = 9.

Pregunta 9. Halla la ecuación del plano que pasa por el punto (1,2,1) y es perpendicular a la recta que une los puntos (1,4,2) y (2,3,5). Encuentre también la distancia perpendicular del origen al plano.

Solución:

La ecuación vectorial de un plano está dada por

$(\vec{r} - \vec{a}).\vec{n} = 0$ …..(1)

Tenemos, $\vec{a} = \hat{i} - 2\hat{j} + \hat{k}$

y, $\vec{n} = \vec{BC} = \hat{i} - \hat{j} + 3\hat{k}$

Poniendo $\vec{a}$ y $\vec{n}$ en (1), obtenemos

$\vec{r}(\hat{i} - \hat{j} + 3\hat{k}) = 2$ ….(2)

$|\vec{n}| = \sqrt{(1)^2 + 1^2 + (3)^2} = \sqrt{11}$

Dividiendo (1) por $\sqrt{11}$

$\vec{r}.[\frac{1}{\sqrt11}\hat{i} - \frac{1}{\sqrt11}\hat{j} + \frac{3}{\sqrt11}\hat{k}] = \frac{2}{\sqrt11}$

Por lo tanto, la ecuación vectorial del plano es $\vec{r}.(\hat{i} - \hat{j} + 3\hat{k}) = 2.$

y la forma cartesiana es x – y + 3z – 2 = 0.

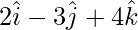Pregunta 10. Encuentra la ecuación vectorial de un plano que está a una distancia de $\frac{6}{\sqrt{29}}$ desde el origen y su vector normal desde el origen es $2\hat{i} - 3\hat{j} + 4\hat{k}$ . Además, encuentre su forma cartesiana.

Solución:

Dado que la ecuación vectorial de un plano de distancia d y normal al vector unitario n viene dada por

$\vec{r}.\hat{n} = d$

Ya que, $|\vec{n}| = \sqrt{(2)^2 + (-3)^2 + (4)^2} = \sqrt{29}$

Vector unitario normal al plano = $\frac{\vec{n}}{|\vec{n}|}$

o, $\hat{n} = \frac{2}{\sqrt29}\hat{i} - \frac{3}{\sqrt29}\hat{j} + \frac{4}{\sqrt29}\hat{k}$

$d = \frac{6}{\sqrt29}$

La ecuación vectorial se convierte en,

$\vec{r}.[\frac{2}{\sqrt29}\hat{i} - \frac{3}{\sqrt29}\hat{j} + \frac{4}{\sqrt29}\hat{k}] = \frac{6}{\sqrt29}$

La ecuación cartesiana es 2x– 3y + 4z = 6.

Pregunta 11. Encuentra la distancia del plano 2x – 3y + 4z – 6 = 0 desde el origen.

Solución:

2x – 3y + 4z – 6 = 0

o, 2x – 3y + 4z = 6

La ecuación vectorial se convierte en,

$(x\hat{i} + y\hat{j} + z\hat{k}).(2\hat{i} - 3\hat{j} + 4\hat{k}) = 6$

o, $\vec{r}.(2\hat{i} - 3\hat{j} + 4\hat{k}) = 6$ …..(1)

$|\vec{n}| = \sqrt{(2)^2 + (-3)^2 + (4)^2} = \sqrt{29}$

Dividiendo (1) por $|\vec{n}|$ , la forma normal de la ecuación se convierte en,

$\vec{r}.[\frac{2}{\sqrt29}\hat{i} - \frac{3}{\sqrt29}\hat{j} + \frac{4}{\sqrt29}\hat{k}] = \frac{6}{\sqrt29}$

Por lo tanto, la distancia perpendicular del origen al plano es $\frac{6}{\sqrt29}$ unidades .

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra la ecuación vectorial de un plano que está a una distancia de 3 unidades del origen y tiene como vector unitario normal a él.

Pregunta 2. Encuentra la ecuación vectorial de un plano que está a una distancia de 5 unidades del origen y que es normal al vector

Pregunta 3. Reduzca la ecuación 2x ​​– 3y – 6z = 14 a la forma normal y, por lo tanto, encuentre la longitud de la perpendicular desde el origen hasta el plano. Además, encuentre la dirección de los cosenos de la normal al plano.

Pregunta 4. Reduzca la ecuación a la forma normal y, por lo tanto, encuentre la longitud de la perpendicular desde el origen hasta el plano.

Pregunta 5. Escribe la forma normal de la ecuación 2x ​​– 3y + 6z + 14 = 0.

Pregunta 6. Las relaciones de dirección de la perpendicular desde el origen a un plano son 12, -3, 4 y la longitud de la perpendicular es 5. Encuentra la ecuación del plano.

Pregunta 7. Encuentra el vector unitario normal al plano x + 2y + 3z – 6 = 0.

Pregunta 8. Encuentra la ecuación de un plano que está a una distancia de unidades del origen y la normal a la que está igualmente inclinada con los ejes de coordenadas.

Pregunta 9. Halla la ecuación del plano que pasa por el punto (1,2,1) y es perpendicular a la recta que une los puntos (1,4,2) y (2,3,5). Encuentre también la distancia perpendicular del origen al plano.

Pregunta 10. Encuentra la ecuación vectorial de un plano que está a una distancia de desde el origen y su vector normal desde el origen es . Además, encuentre su forma cartesiana.

Pregunta 11. Encuentra la distancia del plano 2x – 3y + 4z – 6 = 0 desde el origen.

Deja una respuesta Cancelar la respuesta

Pregunta 1. Encuentra la ecuación vectorial de un plano que está a una distancia de 3 unidades del origen y tiene $\hat{k}$ como vector unitario normal a él.

Pregunta 2. Encuentra la ecuación vectorial de un plano que está a una distancia de 5 unidades del origen y que es normal al vector $\hat{i} - 2\hat{j} - 2\hat{k}.$

Pregunta 3. Reduzca la ecuación 2x – 3y – 6z = 14 a la forma normal y, por lo tanto, encuentre la longitud de la perpendicular desde el origen hasta el plano. Además, encuentre la dirección de los cosenos de la normal al plano.

Pregunta 4. Reduzca la ecuación $\vec{r}.(\hat{i} - 2\hat{j} + 2\hat{k}) + 6 = 0$ a la forma normal y, por lo tanto, encuentre la longitud de la perpendicular desde el origen hasta el plano.

Pregunta 5. Escribe la forma normal de la ecuación 2x – 3y + 6z + 14 = 0.

Pregunta 8. Encuentra la ecuación de un plano que está a una distancia de $3\sqrt{3}$ unidades del origen y la normal a la que está igualmente inclinada con los ejes de coordenadas.

Pregunta 10. Encuentra la ecuación vectorial de un plano que está a una distancia de $\frac{6}{\sqrt{29}}$ desde el origen y su vector normal desde el origen es $2\hat{i} - 3\hat{j} + 4\hat{k}$ . Además, encuentre su forma cartesiana.