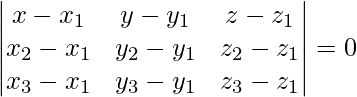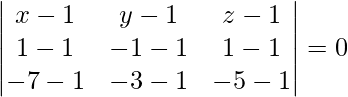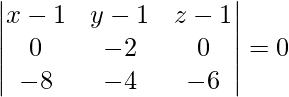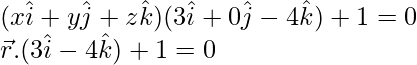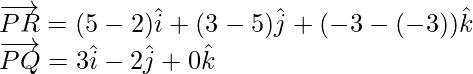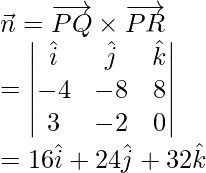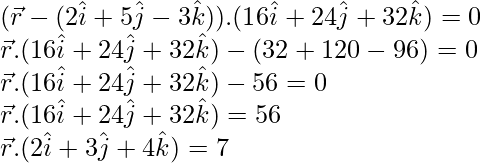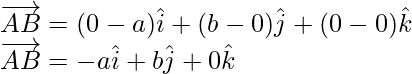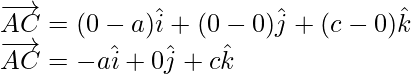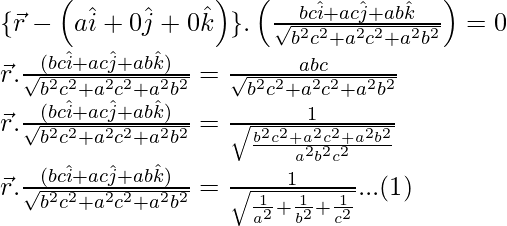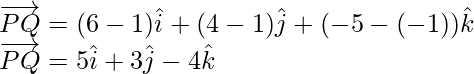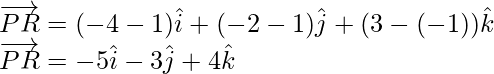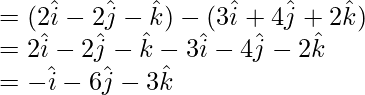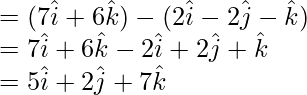Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.5

Posted on by Rudeus Greyrat

Pregunta 1. Encuentra la ecuación vectorial del plano que pasa por los puntos (1, 1, 1), (1, -1, 1) y (-7, -3, -5)

Solución:

Dado que, el avión está pasando

(1, 1, 1), (1, -1, 1) y (-7, -3, -5)

Sabemos que, ecuación del plano que pasa por 3 puntos,

\begin{vmatrix}x-x_1 & y-y_1 & z-z_1\\ x_2-x_1 & y_2-y_1 & z_2-z_1\\ x_3-x_1 & y_3-y_1 & z_3-z_1\end{vmatrix}=0

\begin{vmatrix}x-1 & y-1 & z-1\\ 1-1 & -1-1 & 1-1\\ -7-1 & -3-1 & -5-1\end{vmatrix}=0

\begin{vmatrix}x-1 & y-1 & z-1\\ 0 & -2 & 0\\ -8 & -4 & -6\end{vmatrix}=0

(x – 1)(12 – 0) – (y – 1)(0 – 0) + (z – 1)(0 – 16) = 0

(x – 1)(12) – (y – 1)(0) + (z – 1)(-16) = 0

12x – 12 – 0 – 16z + 16 = 0

12x – 16z + 4 = 0

Dividiendo por 4,

3x – 4z + 1 = 0

(x\hat{i}+y\hat{j}+z\hat{k})(3\hat{i}+0\hat{j}-4\hat{k})+1=0\\ \vec{r}.(3\hat{i}-4\hat{k})+1=0

Ecuación del plano requerido,

\vec{r}.(3\hat{i}-4\hat{k})+1=0

Pregunta 2. Encuentra la ecuación vectorial del plano que pasa por los puntos P(2, 5, -3), Q(-2, -3, 5) y R(5, 3, -3).

Solución:

Sean P(2, 5, -3), Q(-2, -3, 5) y R(5, 3, -3) los tres puntos en un plano que tienen vectores de posición  \vec{p},\vec{q}\ and\ \vec{s}  respectivamente. Entonces los vectores  \overrightarrow{PQ}  y  \overrightarrow{PR}  están en el mismo plano. Por tanto,  \overrightarrow{PQ}\times\overrightarrow{PR}  es un vector perpendicular al plano.

Sea = \vec{n} = \overrightarrow{PQ}\times\overrightarrow{PR}

\overrightarrow{PQ}=(-2-2)\hat{i}+(-3-5)\hat{j}+(5-(-3))\hat{k}\\ \overrightarrow{PQ}=-4\hat{i}-8\hat{j}+8\hat{k}  

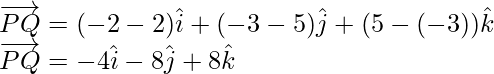
Similarmente,

\overrightarrow{PR}=(5-2)\hat{i}+(3-5)\hat{j}+(-3-(-3))\hat{k}\\ \overrightarrow{PQ}=3\hat{i}-2\hat{j}+0\hat{k}

De este modo 

\vec{n}=\overrightarrow{PQ}\times\overrightarrow{PR}\\ =\begin{vmatrix}\hat{i} & \hat{j} & \hat{k}\\ -4 & -8 & 8\\ 3 & -2 & 0\end{vmatrix}\\ =16\hat{i}+24\hat{j}+32\hat{k}

El plano pasa por el punto P con vector de posición \vec{p}=2\hat{i}+5\hat{j}-3\hat{k}

Por lo tanto, su ecuación vectorial es 

(\vec{r}-(2\hat{i}+5\hat{j}-3\hat{k})).(16\hat{i}+24\hat{j}+32\hat{k})=0\\
(\vec{r}-(2\hat{i}+5\hat{j}-3\hat{k})).(16\hat{i}+24\hat{j}+32\hat{k})=0\\ ⇒\vec{r}.(16\hat{i}+24\hat{j}+32\hat{k})-(32+120-96)=0\\ ⇒\vec{r}.(16\hat{i}+24\hat{j}+32\hat{k})-56=0\\ ⇒\vec{r}.(16\hat{i}+24\hat{j}+32\hat{k})=56\\ ⇒\vec{r}.(2\hat{i}+3\hat{j}+4\hat{k})=7

Pregunta 3. Encuentra la ecuación vectorial del plano que pasa por los puntos A(a, 0, 0), B(0, b, 0) y C(0, 0, c). Reducirlo a su forma normal. Si el plano ABC está a una distancia p del origen, demuestre que 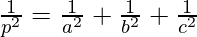\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}

Solución: 

Sean A(a, 0, 0), B(0, b, 0) y C(0, 0, c) tres puntos en un plano que tienen sus vectores de posición  \vec{a},\vec{b}\ and\ \vec{c}  respectivamente. Entonces los vectores  \overrightarrow{AB}  y  \overrightarrow{AC}  están en el mismo plano. Por tanto,  \overrightarrow{AB}\times\overrightarrow{AC}  es un vector perpendicular al plano.

Dejar \vec{n} = \overrightarrow{AB}\times\overrightarrow{AC}

\overrightarrow{AB}=(0-a)\hat{i}+(b-0)\hat{j}+(0-0)\hat{k}\\ \overrightarrow{AB}=-a\hat{i}+b\hat{j}+0\hat{k}

Similarmente,

\overrightarrow{AC}=(0-a)\hat{i}+(0-0)\hat{j}+(c-0)\hat{k}\\ \overrightarrow{AC}=-a\hat{i}+0\hat{j}+c\hat{k}

De este modo

\vec{n} = \overrightarrow{AB}\times\overrightarrow{AC}

      \hat{i}\ \ \ \hat{j}\ \ \ \hat{k}

= | -a b 0 |

       -a 0c

\vec{n}=bc\hat{i}+ac\hat{j}+ab\hat{k}

⇒\hat{n}=\frac{bc\hat{i}+ac\hat{j}+ab\hat{k}}{\sqrt{b^2c^2+a^2c^2+a^2b^2}}

El plano pasa por el punto P con vector de posición \vec{a}=a\hat{i}+0\hat{j}+0\hat{k}

Por lo tanto, la ecuación vectorial en la forma normal es

\{\vec{r}-\left(a\hat{i}+0\hat{j}+0\hat{k}\right)\}.\left(\frac{bc\hat{i}+ac\hat{j}+ab\hat{k}}{\sqrt{b^2c^2+a^2c^2+a^2b^2}}\right)=0\\ ⇒\vec{r}.\frac{(bc\hat{i}+ac\hat{j}+ab\hat{k})}{\sqrt{b^2c^2+a^2c^2+a^2b^2}}=\frac{abc}{\sqrt{b^2c^2+a^2c^2+a^2b^2}}\\ ⇒\vec{r}.\frac{(bc\hat{i}+ac\hat{j}+ab\hat{k})}{\sqrt{b^2c^2+a^2c^2+a^2b^2}}=\frac{1}{\sqrt{\frac{b^2c^2+a^2c^2+a^2b^2}{a^2b^2c^2}}}\\ ⇒\vec{r}.\frac{(bc\hat{i}+ac\hat{j}+ab\hat{k})}{\sqrt{b^2c^2+a^2c^2+a^2b^2}}=\frac{1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}}...(1)

La ecuación vectorial de un plano normal al vector unitario  \hat{n}  ya una distancia ‘d’ del origen es  \vec{r}.\hat{n}=d  ….(2).

Dado que el plano está a una distancia ‘p’ del origen.

Comparando las ecuaciones (1) y (2), tenemos,

re = pag = \frac{1}{\sqrt{\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}}}\\ ⇒\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}

Pregunta 4. Encuentra la ecuación vectorial del plano que pasa por los puntos (1, 1, -1), (6, 4, -5) y (-4, -2, 3).

Solución:

Sean P(1, 1, -1), Q(6, 4, -5) y R(-4, -2, 3) tres puntos en un plano que tienen vectores de posición  \vec{p},\ \vec{q}\ and\ \vec{s}  respectivamente. Entonces los vectores  \overrightarrow{PQ}\ and\ \overrightarrow{PR}  están en el mismo plano. Por tanto,  \overrightarrow{PQ}\times\overrightarrow{PR}  es un vector perpendicular al plano.

Dejar \vec{n}=\overrightarrow{PQ}\times\overrightarrow{PR}

\overrightarrow{PQ}=(6-1)\hat{i}+(4-1)\hat{j}+(-5-(-1))\hat{k}\\ \overrightarrow{PQ}=5\hat{i}+3\hat{j}-4\hat{k}

Similarmente,

\overrightarrow{PR}=(-4-1)\hat{i}+(-2-1)\hat{j}+(3-(-1))\hat{k}\\ \overrightarrow{PR}=-5\hat{i}-3\hat{j}+4\hat{k}

De este modo

Aquí, \overrightarrow{PQ}=-\overrightarrow{PR}

Por lo tanto, los puntos dados son colineales.

Así,  \vec{n}=a\hat{i}+b\hat{j}+c\hat{k}  donde, 5a + 3b – 4c = 0

El plano pasa por el punto P con vector de posición \vec{p}=\hat{i}+\hat{j}-\hat{k}

Por lo tanto, su ecuación vectorial es

\{\vec{r}-(\hat{i}+\hat{j}-\hat{k})\}.(a\hat{i}+b\hat{j}+c\hat{k})=0  , donde, 5a + 3b – 4c = 0

Pregunta 5. Encuentra la ecuación vectorial del plano que pasa por los puntos.

3\hat{i}+4\hat{j}+2\hat{k},\ 2\hat{i}-2\hat{j}-\hat{k}\ \ and\ \ 7\hat{i}+6\hat{k}

Solución:

Sean A, B, C los puntos con vector de posición (3\hat{i}+4\hat{j}+2\hat{k}),(2\hat{i}-2\hat{j}-\hat{k})\ and\ (7\hat{i}+6\hat{k})

respectivamente. Después

\overrightarrow{AB}  = Vector de posición de B – Vector de posición de A

=(2\hat{i}-2\hat{j}-\hat{k})-(3\hat{i}+4\hat{j}+2\hat{k})\\ =2\hat{i}-2\hat{j}-\hat{k}-3\hat{i}-4\hat{j}-2\hat{k}\\ =-\hat{i}-6\hat{j}-3\hat{k}

\overrightarrow{BC}   = Vector de posición de C – Vector de posición de B

=(7\hat{i}+6\hat{k})-(2\hat{i}-2\hat{j}-\hat{k})\\ =7\hat{i}+6\hat{k}-2\hat{i}+2\hat{j}+\hat{k}\\ =5\hat{i}+2\hat{j}+7\hat{k}

Un vector normal a A, B, C es un vector perpendicular a \overrightarrow{AB}\times\overrightarrow{BC}

\vec{n}=\overrightarrow{AB}\times\overrightarrow{BC}\\ =\begin{vmatrix}\hat{i}&\hat{j}&\hat{k}\\ -1&-6&-3\\ 5&2&7\end{vmatrix}\\ \vec{n}=\hat{i}(-42+6)-\hat{j}(-7+15)+\hat{k}(-2+30)\\ =-36\hat{i}-8\hat{j}+28\hat{k}

Como sabemos, la ecuación de un plano que pasa por el vector  \vec{a}  y es perpendicular al vector  \vec{n}  está dada por,

\vec{r}.\vec{n}=\vec{a}.\vec{n}\ \ \ ...(1)

Poner  \vec{a}  y  \vec{n}  en la ecuación (1)

\vec{r}.(-36\hat{i}-8\hat{j}+28\hat{k})=(3\hat{i}+4\hat{j}+2\hat{k})(-36\hat{i}-8\hat{j}+28\hat{k})

= (3)(-36) + (4)(-8) + (2)(28)

= -108 – 32 + 56

= -140 + 56

\vec{r}.(-36\hat{i}-8\hat{j}+28\hat{k})  = -84

Dividiendo por (-4), obtenemos

\vec{r}.(9\hat{i}+2\hat{j}-7\hat{k})=21

La ecuación del plano requerido es,

\vec{r}.(9\hat{i}+2\hat{j}-7\hat{k})=21

Publicación traducida automáticamente

Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *