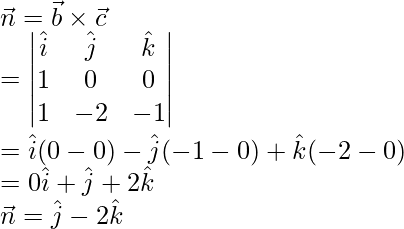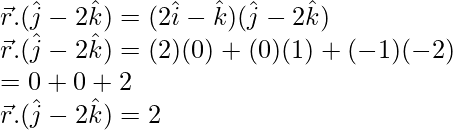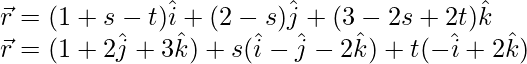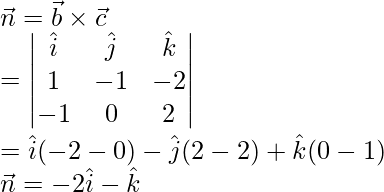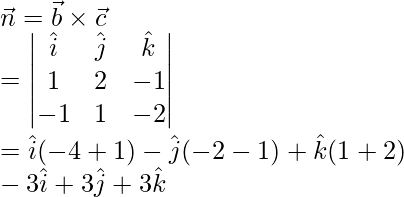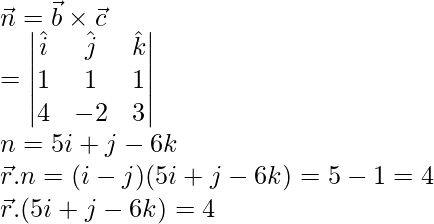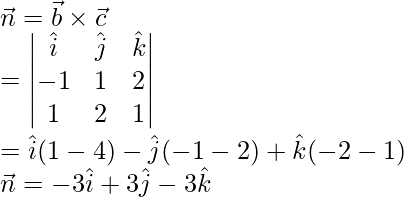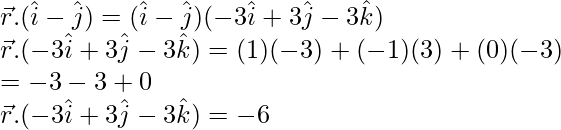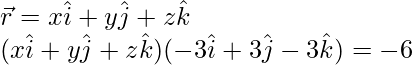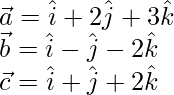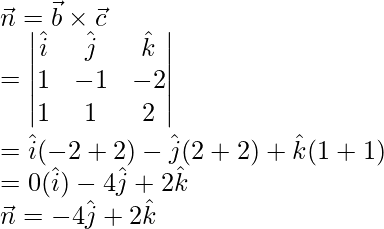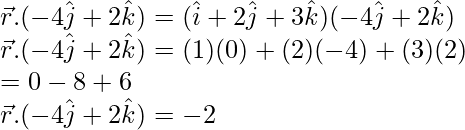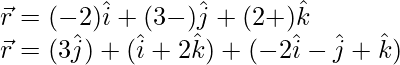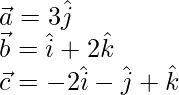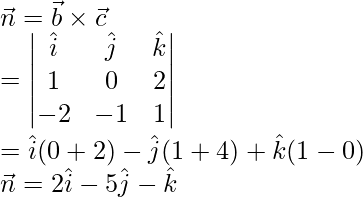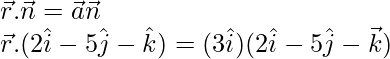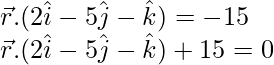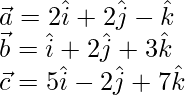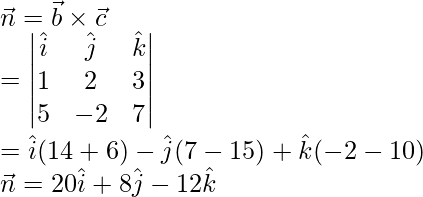Pregunta 1. Encuentra la ecuación vectorial de los siguientes planos en forma de producto escalar 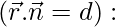
Solución:
(i)
Aquí,
Sabemos que
representamos un plano que pasa por un punto que tiene posición vectorial
y paralelo a los vectores
y .
Aquí,
El plano dado es perpendicular a un vector.
Sabemos que la ecuación vectorial del plano en forma de producto escalar es,
—(Ecuación-1)
Poner
y
entrar (Ecuación-1),
La ecuación se requiere forma es,
(ii)
Aquí,
Sabemos que,
representamos un plano que pasa por un punto que tiene posición vectorial
y paralelo a los vectores
y
Aquí,
El plano dado es perpendicular a un vector.
Sabemos que, la ecuación vectorial de un plano es producto escalar es,
—(Ecuación-1)
Poner valor de
y
en (Ecuación-1)
Multiplicando ambos lados por (-1),
La ecuación en la forma requerida,
(iii)
Dada, ecuación del plano,
Sabemos que,
es la ecuación de un plano que pasa por un punto
y paralelo a
y
.
Aquí,
El plano dado es perpendicular a un vector.
Sabemos que, la ecuación del plano en forma de producto escalar está dada por,
Dividiendo por 3, obtenemos
La ecuación en forma requerida es,
(iv)
El avión pasa a través
y es paralelo a b
y
Pregunta 2. Encuentra la forma cartesiana de la ecuación de los siguientes planos:
Solución:
(i)
Aquí, dada la ecuación del plano es,
Sabemos que,
representa la ecuación de un plano que pasa por un vector
y paralelo al vector
y
.
Aquí,
El plano dado es perpendicular al vector.
Sabemos que, ecuación de plano en forma de producto escalar,
—Ecuación-1
Ponga el valor de
y
en la Ecuación-1,
Poner
(x)(-3) + (y)(3) + (z)(-3) = -6
-3x + 3y – 3z = -6
Dividiendo por (-3), obtenemos
x – y + z = 2
La ecuación en forma requerida es,
x – y + z = 2
(ii)
Dada, ecuación del plano,
Sabemos que,
representa la ecuación de un plano que pasa por el vector
y paralelo al vector
y
Aquí,
El plano dado es perpendicular al vector.
Sabemos que, la ecuación del plano en forma de producto escalar está dada por,
—Ecuación-1
Poner, el valor de
y
en la ecuación-1
Poner
(x)(0) + (y)(-4) + (z)(2) = -2
-4y + 2z = -2
La ecuación en forma requerida es,
2y – z = 1
Pregunta 3. Encuentra la ecuación vectorial de los siguientes planos en forma no paramétrica:
Solución:
(i)
Dada, la ecuación del plano es,
Sabemos que,
representa la ecuación de un plano que pasa por un punto
y es paralelo al vector
y
.
Dado,
El plano dado es perpendicular a
La ecuación vectorial del plano en forma no paramétrica es.
= (0)(2) + (3)(-5) + (0)(-1)
= 0 – 15 + 0
La forma requerida de la ecuación es,
(ii)
Dada, la ecuación del plano es,
Sabemos que,
representa la ecuación de un plano que pasa por un vector
y paralelo al vector
y
.
Aquí,
El plano dado es perpendicular al vector.
Sabemos que, la ecuación de un plano en forma no paramétrica viene dada por,
= (2)(20) + (2)(8) – (-1)(-12)
=40 + 16 + 12
Dividiendo por 4,
La ecuación del plano en forma requerida es,
Publicación traducida automáticamente
Artículo escrito por mallikagupta90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA