Clase 12 RD Sharma Solutions – Capítulo 29 El avión – Ejercicio 29.8

Pregunta 1. Encuentra la ecuación del plano que es paralelo a 2x – 3y + z = 0 y pasa por el punto (1, –1, 2).

Solución:

Sabemos que la ecuación de un plano paralelo a 2x – 3y + z = 0 viene dada por:

2x – 3y + z + λ = 0

Como el plano pasa por el punto (1, –1, 2), tenemos:

2(1) – 3(–1) + 2 + λ = 0

⇒ λ = –7

Al sustituir el valor de λ en la ecuación, tenemos:

2x – 3y + z + (-7) = 0

2x – 3y + z – 7= 0 es la ecuación requerida.

Pregunta 2. Encuentra la ecuación del plano que pasa por (3, 4, –1) que es paralelo al plano 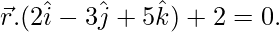$\vec{r}.(2\hat{i}-3\hat{j}+5\hat{k})+2=0.$

Solución:

El plano dado pasa por el vector $3\hat{i}+4\hat{j}-\hat{k}$ . De este modo,

$(3\hat{i}+4\hat{j}-\hat{k}).(2\hat{i}-3\hat{j}+5\hat{k})+ λ=0.$

(3)(2) + (4)(-3) + (-1)(5) + λ = 0

⇒ λ = 11

Al sustituir el valor de λ en la ecuación, tenemos:

$\vec{r}.(2\hat{i}-3\hat{j}+5\hat{k})+11=0$ es la ecuación requerida.

Pregunta 3. Encuentra la ecuación del plano que pasa por la línea de intersección de los planos 2x – 7y + 4z – 3 = 0 y 3x – 5y + 4z + 11 = 0 y el punto (–2, 1, 3).

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:
(2x – 7y + 4z – 3) + λ(3x – 5y + 4z + 11) = 0

⇒ x(2 + 3λ) + y(–7 – 5λ) + z(4 + 4λ) – 3 + 11λ = 0

Además, como el plano pasa por el punto (–2, 1, 3), tenemos:

(–2)(2 + 3λ) + (1)(–7 – 5λ) + (3)(4 + 4λ) – 3 + 11λ = 0

⇒ λ = 1/6

Al sustituir el valor de λ en la ecuación, tenemos:

x(2 + 3(1/6)) + y(–7 – 5(1/6)) + z(4 + 4(1/6)) – 3 + 11(1/6) = 0

15x – 47y + 28z = 7 es la ecuación requerida.

Pregunta 4. Encuentra la ecuación del plano que pasa por el punto 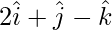$2\hat{i}+\hat{j}-\hat{k}$ y pasa por la línea de intersección de los planos 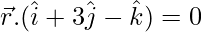$\vec{r}.(\hat{i}+3\hat{j}-\hat{k})=0$ y $\vec{r}.(\hat{j}+\hat{k})=0.$

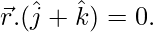
Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

$\vec{r}.[(\hat{i}+3\hat{j}-\hat{k})+λ(\hat{j}+2\hat{k})]=0$

Además, como el plano pasa por el punto $2\hat{i}+\hat{j}-\hat{k}$ , tenemos:

$(2\hat{i}+\hat{j}-\hat{k})(\hat{i}+3\hat{j}-\hat{k})+λ(2\hat{i}+\hat{j}-\hat{k})(\hat{j}+2\hat{k})=0$

⇒ λ = 6

Al sustituir el valor de λ en la ecuación, tenemos:

$\vec{r}.(\hat{i}+9\hat{j}+11\hat{k})=0$ es la ecuación requerida.

Pregunta 5. Encuentra la ecuación del plano que pasa por la intersección de 2x – y = 0 y 3z – y = 0 y perpendicular a 4x + 5y – 3z = 8.

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

2x – y + λ(3z – y) = 0

⇒ 2x + y(–1 – λ) + z(3λ) = 0

Como los planos son perpendiculares, tenemos:

2(4) + (–5)(–1 – λ) + (–3)(3λ) = 0

⇒ λ = 3/14

Al sustituir el valor de λ en la ecuación, tenemos:

2x + y(–1 – 3/14) + z(3(3/14)) = 0

28x – 17y + 9z = 0 es la ecuación requerida.

Pregunta 6. Encuentra la ecuación del plano que contiene la línea de intersección de los planos x + 2y + 3z – 4 = 0 y 2x + y – z + 5 = 0 y es perpendicular al plano 5x + 3y – 6z + 8 = 0.

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

x + 2y + 3z – 4 + λ(2x + y – z + 5) = 0

⇒ x(1 + 2λ) + y(2 + λ) + z(3 – λ) – 4 + 5λ = 0

Como los planos son perpendiculares, tenemos:

5(1 + 2λ) + 3(2 + λ) + (–6)(3 – λ) = 0

⇒ λ = 7/19

Al sustituir el valor de λ en la ecuación, tenemos:

x(1 + 2(7/19)) + y(2 + 7/19) + z(3 – 7/19) – 4 + 5(7/19) = 0

33x + 45y + 50z – 41 = 0 es la ecuación requerida.

Pregunta 7. Encuentra la ecuación del plano que pasa por la línea de intersección de los planos x + 2y + 3z + 4 = 0 y x – y + z + 3 = 0 y pasa por el origen.

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

x + 2y + 3z + 4 + λ(x – y + z + 3) = 0

⇒ x(1 + λ) + y(2 – λ) + z(3 + λ) + 4 + 3λ = 0

Además, como el plano pasa por el origen, tenemos:

0(1 + λ) + 0(2 – λ) + 0(3 + λ) + 4 + 3λ = 0

⇒ λ = -4/3

Al sustituir el valor de λ en la ecuación, tenemos:

x(1 + (-4/3)) + y(2 – (-4/3)) + z(3 + (-4/3)) + 4 + 3(-4/3) = 0

x – 10y – 5z = 0 es la ecuación requerida.

Pregunta 8. Encuentra la ecuación vectorial en forma de producto escalar del plano que contiene la línea de intersección de los planos x – 3y + 2z – 5 = 0 y 2x – y + 3z – 1 = 0 y que pasa por (1, –2, 3).

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

x – 3y + 2z – 5 + λ(2x – y + 3z – 1) = 0

⇒ x(1 + 2λ) + y(–3 – λ) + z(2 + 3λ) – 5 – λ = 0

Además, como el plano pasa por el origen, tenemos:

1(1 + 2λ) + (–2)(–3 – λ) + 3(2 + 3λ) – 5 – λ = 0

⇒ λ = -2/3

Al sustituir el valor de λ en la ecuación, tenemos:

x(1 + 2(-2/3)) + y(–3 – (-2/3)) + z(2 + 3(-2/3)) – 5 – (-2/3) = 0

$\vec{r}.(\hat{i}+7\hat{j})+13=0$ es la ecuación requerida.

Pregunta 9. Encuentra la ecuación del plano que contiene la línea de intersección de los planos x + 2y + 3z – 4 = 0 y 2x + y – z + 5 = 0 y es perpendicular al plano 5x + 3y + 6z + 8 = 0.

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

x + 2y + 3z – 4 + λ(2x + y – z + 5) = 0

⇒ x(1 + 2λ) + y(2 + λ) + z(3 – λ) – 4 + 5λ = 0

Sabemos que dos planos son perpendiculares cuando $a_1a_2+b_1b_2+c_1c_2=0.$

⇒ 5(1 + 2λ) + 3(2 + λ) + 6(3 – λ) = 0

⇒ λ = -29/7

Al sustituir el valor de λ en la ecuación, tenemos:

x(1 + 2(-29/7)) + y(2 + (-29/7)) + z(3 – (-29/7)) – 4 + 5(-29/7) = 0

51x + 15y – 50z + 173 = 0 es la ecuación requerida.

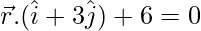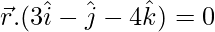Pregunta 10. Encuentra la ecuación del plano que pasa por la línea de intersección de los planos $\vec{r}.(\hat{i}+3\hat{j})+6=0$ y $\vec{r}.(3\hat{i}-\hat{j}-4\hat{k})=0$ y que está a una unidad de distancia del origen.

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

x(1 + 3λ) + y(3 + λ) – 4zλ + 6 = 0

Distancia del plano al origen = 1

⇒ $|\frac{6}{\sqrt{(1+3λ )^2+(3-λ)^2+(4λ)^2}}|=1$

⇒ λ = ±1

Por lo tanto, 4x + 2y – 4z + 6 = 0 y –2x + 2y + 4z + 6 = 0 son las ecuaciones requeridas.

Pregunta 11. Encuentra la ecuación del plano que pasa por la línea de intersección de los planos 2x + 3y – z + 1 = 0 y x + y – 2z + 3 = 0 y perpendicular al plano 3x – 2y – z – 4 = 0.

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

2x + 3y – z + 1 + λ(x + y – 2z + 3) = 0

⇒ x(2 + λ) + y(3 + λ) + z(–1 – 2λ) + 1 + 3λ = 0

Sabemos que dos planos son perpendiculares cuando $a_1a_2+b_1b_2+c_1c_2=0.$

⇒ 3(2 + λ) + (–1)(3 + λ) + (–2)(–1 – 2λ) = 0

⇒ λ = -5/6

Al sustituir el valor de λ en la ecuación, tenemos:

x(2 + (-5/6)) + y(3 + (-5/6)) + z(–1 – 2(-5/6)) + 1 + 3(-5/6) = 0

7x + 13y + 4z – 9 = 0 es la ecuación requerida.

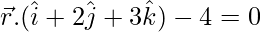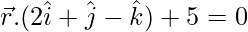Pregunta 12. Encuentra la ecuación del plano que contiene la línea de intersección de los planos $\vec{r}.(\hat{i}+2\hat{j}+3\hat{k})-4=0$ y $\vec{r}.(2\hat{i}+\hat{j}-\hat{k})+5=0$ y que es perpendicular al plano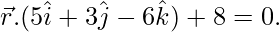 $\vec{r}.(5\hat{i}+3\hat{j}-6\hat{k})+8=0.$

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

$\vec{r}.(\hat{i}+2\hat{j}+3\hat{k})-4+λ(\vec{r}.(2\hat{i}+\hat{j}-\hat{k})+5)=0$

⇒ $\vec{r}.[(\hat{i}+2\hat{j}+3\hat{k})+λ(2\hat{i}+\hat{j}-\hat{k})]-4+5λ=0$

Sabemos que dos planos son perpendiculares si $\vec{n_1}.\vec{n_2}=0$

⇒ $[(\hat{i}+2\hat{j}+3\hat{k})+λ(2\hat{i}+\hat{j}-\hat{k})](5\hat{i}+3\hat{j}-6\hat{k})=0$

⇒ 5(1 + 2λ) + 3(2 + λ) + (–6)(3 – λ) = 0

⇒ λ = 7/19

Al sustituir el valor de λ en la ecuación, tenemos:

33x + 45y + 50z – 41 = 0 es la ecuación requerida.

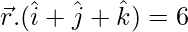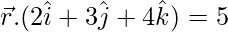Pregunta 13. Encuentra la ecuación vectorial del plano que pasa por la intersección de los planos $\vec{r}.(\hat{i}+\hat{j}+\hat{k})=6$ y $\vec{r}.(2\hat{i}+3\hat{j}+4\hat{k})=5$ el punto (1, 1, 1).

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

$\vec{r}.(\hat{i}+\hat{j}+\hat{k})-6+λ(\vec{r}.(2\hat{i}+3\hat{j}+4\hat{k})-5)=0$

⇒ x(1 + 2λ) + y(1 + 3λ) +z(1 + 4λ) = 6 – 5λ

Además, como el plano pasa por el punto (1, 1, 1), tenemos:

1(1 + 2λ) + 1(1 + 3λ) +1(1 + 4λ) = 6 – 5λ

⇒ λ = 3/14

Al sustituir el valor de λ en la ecuación, tenemos:

x(1 + 2(3/14)) + y(1 + 3(3/14)) +z(1 + 4(3/14)) = 6 – 5(3/14)

$\vec{r}.(20\hat{i}+23\hat{j}+26\hat{k})=69$ es la ecuación requerida.

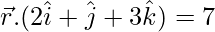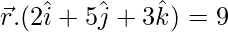Pregunta 14. Encuentra la ecuación del plano que pasa por la intersección de los planos $\vec{r}.(2\hat{i}+\hat{j}+3\hat{k})=7$ y $\vec{r}.(2\hat{i}+5\hat{j}+3\hat{k})=9$ y el punto (2, 1, 3).

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

$\vec{r}.(2\hat{i}+\hat{j}+3\hat{k})-7+λ(\vec{r}.(2\hat{i}+5\hat{j}+3\hat{k})-9)=0$

⇒ $\vec{r}.[(2+2λ)\hat{i}+(1+5λ)\hat{j}+(3+3λ)\hat{k}]-7-9λ=0$

Además, como el plano pasa por el punto (2, 1, 3) tenemos:

9λ = –7

⇒ λ = -7/9

Sustituyendo el valor de λ en la ecuación, tenemos:

$\vec{r}.(2\hat{i}-13\hat{j}+3\hat{k})=0$ es la ecuación requerida.

Pregunta 15. Encuentra la ecuación del plano que pasa por la intersección de los planos 3x – y + 2z = 4 y x + y + z = 2 y el punto (2, 2, 1).

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

3x – y + 2z – 4 + λ(x + y + z – 2) = 0

Además, como el plano pasa por el punto (2, 2, 1), tenemos:

λ = -2/3

Al sustituir el valor de λ en la ecuación, tenemos:

3x – y + 2z – 4 + (-2/3)(x + y + z – 2) = 0

7x – 5y + 4z = 0 es la ecuación requerida.

Pregunta 16. Encuentra la ecuación vectorial del plano a través de la línea de intersección de los planos x + 2y + z = 1 y 2x + 3y + 4z = 5 que es perpendicular al plano x – y + z = 0.

Solución:

La ecuación del plano que pasa por la línea de intersección de los planos dados es:

x + 2y + z – 1 + λ(2x + 3y + 4z – 5) = 0

⇒ x(1 + 2λ) + y(1 + 3λ) +z(1 + 4λ) = 1 + 5λ

Sabemos que dos planos son perpendiculares cuando $a_1a_2+b_1b_2+c_1c_2=0.$

⇒ 1(1 + 2λ) + (–1)(1 + 3λ) + 1(1 + 4λ) = 1 + 5λ

⇒ λ = -1/3

Al sustituir el valor de λ en la ecuación, tenemos:

x(1 + 2(-1/3)) + y(1 + 3(-1/3)) + z(1 + 4(-1/3)) = 1 + 5(-1/3)

x – z + 2 = 0 es la ecuación requerida.

Pregunta 17. Encuentra la ecuación del plano que pasa por (a, b, c) y es paralelo al plano 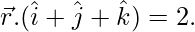$\vec{r}.(\hat{i}+\hat{j}+\hat{k})=2.$

Solución:

Ecuación de la familia de planos paralelos al plano dado = $\vec{r}.(\hat{i}+\hat{j}+\hat{k})=d$

Como el avión pasa por (a, b, c), tenemos:

un + segundo + c = re

Sustituyendo la ecuación anterior en la ecuación de familia de planos tenemos:

$\vec{r}(\hat{i}+\hat{j}+\hat{k})=a+b+c$

Por lo tanto, x + y + z = a + b + c es la ecuación requerida del plano.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra la ecuación del plano que es paralelo a 2x – 3y + z = 0 y pasa por el punto (1, –1, 2).

Pregunta 2. Encuentra la ecuación del plano que pasa por (3, 4, –1) que es paralelo al plano

Pregunta 3. Encuentra la ecuación del plano que pasa por la línea de intersección de los planos 2x – 7y + 4z – 3 = 0 y 3x – 5y + 4z + 11 = 0 y el punto (–2, 1, 3).

Pregunta 4. Encuentra la ecuación del plano que pasa por el punto y pasa por la línea de intersección de los planos y

Pregunta 5. Encuentra la ecuación del plano que pasa por la intersección de 2x – y = 0 y 3z – y = 0 y perpendicular a 4x + 5y – 3z = 8.

Pregunta 6. Encuentra la ecuación del plano que contiene la línea de intersección de los planos x + 2y + 3z – 4 = 0 y 2x + y – z + 5 = 0 y es perpendicular al plano 5x + 3y – 6z + 8 = 0.

Pregunta 7. Encuentra la ecuación del plano que pasa por la línea de intersección de los planos x + 2y + 3z + 4 = 0 y x – y + z + 3 = 0 y pasa por el origen.

Pregunta 8. Encuentra la ecuación vectorial en forma de producto escalar del plano que contiene la línea de intersección de los planos x – 3y + 2z – 5 = 0 y 2x – y + 3z – 1 = 0 y que pasa por (1, –2, 3).

Pregunta 9. Encuentra la ecuación del plano que contiene la línea de intersección de los planos x + 2y + 3z – 4 = 0 y 2x + y – z + 5 = 0 y es perpendicular al plano 5x + 3y + 6z + 8 = 0.

Pregunta 10. Encuentra la ecuación del plano que pasa por la línea de intersección de los planos y y que está a una unidad de distancia del origen.

Pregunta 11. Encuentra la ecuación del plano que pasa por la línea de intersección de los planos 2x + 3y – z + 1 = 0 y x + y – 2z + 3 = 0 y perpendicular al plano 3x – 2y – z – 4 = 0.

Pregunta 12. Encuentra la ecuación del plano que contiene la línea de intersección de los planos y y que es perpendicular al plano

Pregunta 13. Encuentra la ecuación vectorial del plano que pasa por la intersección de los planos y el punto (1, 1, 1).

Pregunta 14. Encuentra la ecuación del plano que pasa por la intersección de los planos y y el punto (2, 1, 3).

Pregunta 15. Encuentra la ecuación del plano que pasa por la intersección de los planos 3x – y + 2z = 4 y x + y + z = 2 y el punto (2, 2, 1).

Pregunta 16. Encuentra la ecuación vectorial del plano a través de la línea de intersección de los planos x + 2y + z = 1 y 2x + 3y + 4z = 5 que es perpendicular al plano x – y + z = 0.

Pregunta 17. Encuentra la ecuación del plano que pasa por (a, b, c) y es paralelo al plano

Deja una respuesta Cancelar la respuesta

Pregunta 2. Encuentra la ecuación del plano que pasa por (3, 4, –1) que es paralelo al plano $\vec{r}.(2\hat{i}-3\hat{j}+5\hat{k})+2=0.$

Pregunta 4. Encuentra la ecuación del plano que pasa por el punto $2\hat{i}+\hat{j}-\hat{k}$ y pasa por la línea de intersección de los planos $\vec{r}.(\hat{i}+3\hat{j}-\hat{k})=0$ y $\vec{r}.(\hat{j}+\hat{k})=0.$

Pregunta 10. Encuentra la ecuación del plano que pasa por la línea de intersección de los planos $\vec{r}.(\hat{i}+3\hat{j})+6=0$ y $\vec{r}.(3\hat{i}-\hat{j}-4\hat{k})=0$ y que está a una unidad de distancia del origen.

Pregunta 12. Encuentra la ecuación del plano que contiene la línea de intersección de los planos $\vec{r}.(\hat{i}+2\hat{j}+3\hat{k})-4=0$ y $\vec{r}.(2\hat{i}+\hat{j}-\hat{k})+5=0$ y que es perpendicular al plano $\vec{r}.(5\hat{i}+3\hat{j}-6\hat{k})+8=0.$

Pregunta 13. Encuentra la ecuación vectorial del plano que pasa por la intersección de los planos $\vec{r}.(\hat{i}+\hat{j}+\hat{k})=6$ y $\vec{r}.(2\hat{i}+3\hat{j}+4\hat{k})=5$ el punto (1, 1, 1).

Pregunta 14. Encuentra la ecuación del plano que pasa por la intersección de los planos $\vec{r}.(2\hat{i}+\hat{j}+3\hat{k})=7$ y $\vec{r}.(2\hat{i}+5\hat{j}+3\hat{k})=9$ y el punto (2, 1, 3).

Pregunta 17. Encuentra la ecuación del plano que pasa por (a, b, c) y es paralelo al plano $\vec{r}.(\hat{i}+\hat{j}+\hat{k})=2.$