Pregunta 21: Maximiza Z = 3x + 3y, si es posible,
Sujeto a las restricciones
x – y ≤ 1
x + y ≥ 3
x, y ≥ 0
Solución:
Convierta lo dado en ecuaciones en ecuaciones, obtendremos las siguientes ecuaciones:
x − y = 1, x + y = 3, x = 0 y y = 0
El área mostrada por x − y ≤ 1:
La línea x − y = 1 coincide con los ejes de coordenadas en A(1, 0) y B(0, −1) respectivamente.
Después de conectar estos puntos obtendremos la línea x − y = 1.
De este modo,
(0,0) asegurar la ecuación x + y ≤ 8.
De este modo,
El área en el plano xy cuyo origen muestra el conjunto solución del en la ecuación x − y ≤ 1.
El área mostrada por x + y ≥ 3:
La recta x + y = 3 coincide con los ejes de coordenadas en C(3, 0) y D(0, 3) respectivamente.
Después de conectar estos puntos obtendremos la línea x + y = 3.
De este modo,
(0,0) asegura la ecuación x + y ≥ 3.
De este modo,
El área en el plano xy que no tiene origen muestra el conjunto solución de en la ecuación x + y ≥ 3.
El área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Todos los puntos en el primer cuadrante aseguran esto en ecuaciones. Por lo tanto, el primer cuadrante es el área mostrada por las ecuaciones
x ≥ 0 y y ≥ 0.
El área adecuada determinada por el sistema de restricciones x − y ≤ 1, x + y ≥ 3, x ≥ 0 y y ≥ 0 son las siguientes.
El área adecuada es ilimitada.
Obtendremos el valor máximo en el infinito.
Por eso,
El valor máximo será infinito, es decir, la solución no tiene límites.
Pregunta 22. Muestre la zona de solución de las siguientes desigualdades en un papel cuadriculado:
5x + y ≥ 10
x + y ≥ 6
x + 4y ≥ 12
x ≥ 0,
y ≥ 0
Encuentre x e y para los cuales 3x + 2y es mínimo sujeto a estas desigualdades. Usa un método gráfico.
Solución:
Convierta lo dado en ecuaciones en ecuaciones, obtendremos las siguientes ecuaciones:
5x + y = 10, x +y = 6, x + 4y = 12, x = 0 y y = 0
El área mostrada por 5x + y ≥ 10:
La recta 5x + y = 10 coincide con los ejes de coordenadas en A(2, 0) y B(0, 10) respectivamente.
Después de conectar estos puntos obtendremos la línea 5x + y = 10.
De este modo,
(0,0) no asegura el en la ecuación 5x + y ≥ 10.
De este modo,
El área en el plano xy que no tiene origen muestra el conjunto solución de en la ecuación 5x + y ≥ 10.
El área mostrada por x +y ≥ 6:
La recta x +y = 6 coincide con los ejes de coordenadas en C(6,0) y D(0,6) respectivamente.
Después de conectar estos puntos obtendremos la línea 2x +3y = 30.
De este modo,
(0,0) no asegura en la ecuación x +y ≥ 6.
De este modo,
El área que no tiene origen muestra el conjunto solución de en la ecuación 2x +3y ≥ 30.
El área mostrada por x + 4y ≥ 12
La recta x + 4y = 12 coincide con los ejes de coordenadas en E(12, 0) y F(0, 3) respectivamente.
Después de conectar estos puntos obtendremos la línea x + 4y = 12.
De este modo,
(0,0) no asegura en la ecuación x + 4y ≥ 12.
De este modo,
El área que no tiene origen muestra el conjunto solución de en la ecuación x + 4y ≥ 12.
El área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Todos los puntos en el primer cuadrante aseguran esto en ecuaciones. Así, el primer cuadrante es el área mostrada por las inecuaciones
x ≥ 0 y y ≥ 0.
El área adecuada determinada por el sistema de restricciones 5x + y ≥ 10, x +y ≥ 6,x + 4y ≥ 12, x ≥ 0 e y ≥ 0, son las siguientes.
Los puntos de esquina del área adecuada son B(0, 10), G(1,5), H(4,2) y E(12,0).
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 3x + 2y
B (0, 10)
3 × 0 + 3 × 10 = 30
Sol (1,5)
3 × 1 + 2 × 5 = 13
H (4,2)
3 × 4 + 2 × 2 = 16
mi (12,0)
3 × 12 + 2 × 0 = 36
Por eso,
El valor mínimo de Z es 13 en el punto G(1,5).
Por lo tanto,
x = 1 y y = 5 es la mejor solución del LPP dado.
Por lo tanto, el mejor valor de Z es 13.
Pregunta 23: Encuentra el valor máximo y mínimo de 2x + y sujeto a las restricciones:
x + 3y ≥ 6,
x − 3y ≤ 3,
3x + 4y ≤ 24,
− 3x + 2y ≤ 6,
5x + y ≥ 5,
x, y ≥ 0.
Solución:
Convierta lo dado en ecuaciones en ecuaciones, obtendremos las siguientes ecuaciones:
x + y = 4, x + y = 3, x − 2y = 2, x = 0 y y = 0.
La recta x + 3y = 6 coincide con el eje de coordenadas en A(6, 0)A6, 0 y B(0, 2).
Conecta estos puntos para obtener la línea x + 3y = 6.
De este modo,
(0, 0) no asegura el en la ecuación x + 3y ≥ 6. Por lo tanto, el área en el plano xy que no tiene el origen representa el
conjunto solución de la ecuación dada.
La recta x − 3y = 3 coincide con el eje de coordenadas en C(3, 0) y D(0, −1).
Conecta estos puntos para obtener la línea x − 3y = 3.
De este modo,
(0, 0) asegura que en la ecuación x − 3y ≤ 3. Por lo tanto, el área en el plano xy que tiene el origen representa el conjunto solución del dado
ecuación.
La recta 3x + 4y = 24 se encuentra con el eje de coordenadas en E(8, 0) y F(0, 6). Une estos puntos para obtener la línea 3x + 4y = 24.
De este modo,
(0, 0) aseguran que en la ecuación 3x + 4y ≤ 24. Así, el área en el plano xy que tiene el origen muestra el conjunto solución del dado
ecuación.
La recta −3x + 2y = 6 coincide con el eje de coordenadas en G(−2, 0) y H(0, 3).
Conecta estos puntos para obtener la línea −3x + 2y = 6.
Por lo tanto, (0, 0) asegura la ecuación −3x + 2y ≤ 6.
De este modo,
El área en el plano xy que tiene el origen representa el conjunto solución de la ecuación dada.
La línea 5x + y = 5 coincide con el eje de coordenadas en I(1, 0)I1, 0 y J(0, 5).
Conecta estos puntos para obtener la línea 5x + y = 5.
De este modo,
(0, 0) no asegura el en la ecuación 5x + y ≥ 5. Por lo tanto, el área en el plano xy que no tiene el origen tiene el
conjunto solución de la ecuación dada.
El área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Todos los puntos del primer cuadrante aseguran estas inecuaciones. Por lo tanto, el primer cuadrante es el área que muestran las ecuaciones.
Estas líneas están dibujadas usando una escala satisfactoria.
Los puntos de esquina del área adecuada
son P
, K
, L
, M
,
norte
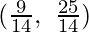
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 2 x + y
PAGS
2 ×
k
2 ×
+ 5 =
L
2 ×
METRO
2 ×
norte
2 ×
Aquí, podemos ver que el valor mínimo de la función objetivo Z es
que está en N
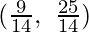
y el valor máximo de la función objetivo es
el que está en L
.
Pregunta 24: Encuentra el valor mínimo de 3x + 5y sujeto a las restricciones
− 2x + y ≤ 4,
x + y ≥ 3,
x − 2y ≤ 2,
x, y ≥ 0.
Solución:
Convierta lo dado en ecuaciones en ecuaciones, obtendremos las siguientes ecuaciones:
−2x + y = 4, x + y = 3, x − 2y = 2, x = 0 y y = 0.
La recta −2x + y = 4 coincide con el eje de coordenadas en A(−2, 0)A-2, 0 y B(0, 4).
Conecta estos puntos para obtener la línea −2x + y = 4.
Por lo tanto, (0, 0) asegura el en la ecuación −2x + y ≤ 4. Entonces, el área en el plano xy que tiene el origen representa el conjunto solución de la
ecuación dada.
La recta x + y = 3 coincide con el eje de coordenadas en C(3, 0) y D(0, 3).
Conecta estos puntos para obtener la línea x + y = 3.
De este modo,
(0, 0) no asegura el en la ecuación x + y ≥ 3. Por lo tanto, el área en el plano xy que no tiene el origen muestra el conjunto solución
de la ecuación dada.
La recta x − 2y = 2 coincide con el eje de coordenadas en E(2, 0) y F(0, −1).
Conecta estos puntos para obtener la línea x − 2y = 2.
De este modo,
(0, 0) asegure el en la ecuación x − 2y ≤ 2. Por lo tanto, el área en el plano xy que tiene el origen representa el conjunto solución del dado
ecuación.
El área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Todos los puntos en el primer cuadrante aseguran esto en ecuaciones. Por lo tanto, el primer cuadrante es el área que muestran las ecuaciones.
Estas líneas están dibujadas usando una escala satisfactoria.
Los puntos de esquina del área adecuada son B(0, 4), D(0, 3) y G
.
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 3 x + 5 y
b(0, 4)
3 × 0+ 5 × 4 = 20
D(0, 3)
3 × 0+ 5 × 3 = 15
GRAMO
3 ×
+ 5 ×
=
Aquí podemos ver que el valor mínimo de la función objetivo Z es el
que está en G.
Por lo tanto,
El mejor valor de Z es
.
Pregunta 25: Resolvió gráficamente el siguiente problema de programación lineal:
Maximizar Z = 60x + 15y
Sujeto a restricciones
x + y ≤ 50
3x + y ≤ 90
x, y≥0
Solución:
Aquí tenemos que maximizar Z = 60x + 15y
Convierta lo dado en ecuaciones en ecuaciones, obtenemos las siguientes ecuaciones:
x + y = 50, 3x + y = 90, x = 0 y y = 0
El área mostrada por x + y ≤ 50:
La línea x + y = 50 coincide con los ejes de coordenadas en A(50,0) y B(0,50) respectivamente.
Después de conectar estos puntos obtendremos la línea 3x + 5y = 15.
De este modo,
(0,0) aseguran la ecuación en x + y ≤ 50. Así, el área que tiene el origen muestra el conjunto solución de la ecuación en x + y ≤ 50.
El área mostrada por 3x + y ≤ 90:
La línea 3x + y = 90 coincide con los ejes de coordenadas en C(30, 0) y D(0, 90) respectivamente.
Después de conectar estos puntos obtendremos la línea 3x + y = 90.
De este modo,
(0,0) asegura que en la ecuación 3x + y ≤ 90. Así, el área que tiene el origen muestra el conjunto solución de la en la ecuación 3x + y ≤ 90.
El área mostrada por x ≥ 0 y y ≥ 0:
Por eso,
Todos los puntos en el primer cuadrante aseguran esto en ecuaciones. Por lo tanto, el primer cuadrante es el área mostrada por las ecuaciones
x ≥ 0 y y ≥ 0.
El área adecuada determinada por el sistema de restricciones, x + y ≤ 50, 3x + y ≤ 90, x ≥ 0 e y ≥ 0, son las siguientes.
Los puntos de esquina del área adecuada son O(0, 0), C(30, 0), E(20, 30) y B(0, 50).
Los valores de Z en estos puntos de esquina son los siguientes.
punto de esquina
Z = 60 x + 15 y
O (0, 0)
60 × 0 + 15 × 0 = 0
C (30, 0)
60 × 30 + 15 × 0 = 1800
E(20, 30)E20, 30
60 × 20 + 15 × 30 = 1650
B (0, 50)
60 × 0 + 15 × 50 = 750
Por eso,
El valor máximo de Z es 1800 en el punto (30, 0) en el punto 30, 0.
Por lo tanto,
x = 30 y y = 0 es la mejor solución del LPP dado.
Por lo tanto,
El mejor valor de Z es 1800.
Pregunta 26. Encuentre gráficamente, el valor máximo de Z = 2x + 5y, sujeto a las restricciones dadas a continuación:
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0 [CBSE 2015]
Solución:
Aquí,
Maximizar Z = 2x + 5y sujeto a las restricciones
2x + 4y ≤ 8
3x + y ≤ 6
x + y ≤ 4
x ≥ 0, y ≥ 0
Después de convertir las ecuaciones en ecuaciones, obtendremos las siguientes ecuaciones de líneas rectas:
2x + 4y = 8, 3x + y = 6, x + y = 4
La línea 2x + 4y = 8 coincide con los ejes de coordenadas en (4, 0) y (0, 2).
La línea 3x + y = 6 coincide con los ejes de coordenadas en (2, 0) y (0, 6).
La línea x + y = 4 coincide con los ejes de coordenadas en (4, 0) y (0, 4).
El área adecuada determinada por las restricciones dadas se puede mostrar esquemáticamente como,
Las coordenadas de los puntos de las esquinas del área adecuada son O(0, 0), A(0, 2), B
y C(2, 0).
El valor de la función objetivo en estos puntos se da en la siguiente tabla.
Punto de esquina
Z = 2x + 5y
(0, 0)
2 × 0 + 5 × 0 = 0
(2, 0)
2 × 2 + 5 × 0 = 4
(0, 2)
2 × 0 + 5 × 2 = 10 → Máximo
2×
+5×
=
Por lo tanto,
El valor máximo de Z es 10 en x = 0, y = 2.
Pregunta 27: Resuelva gráficamente el siguiente LPP:
Maximizar Z = 20x + x + 10y
Sujeto a las siguientes restricciones
x + 2y ≤ 28
3x + y ≤ 24
X ≥ 2
x, y ≥ 0
Solución:
Aquí las restricciones dadas son
x + 2y ≤ 28
3x + y ≤ 24
x ≥ 2
x, y ≥ 0Convirtiendo lo dado en ecuaciones en ecuaciones,
obtendremos
x + 2y = 28, 3x + y = 24, x = 2, x = 0 y y = 0
Estas líneas se dibujan en el gráfico y la región sombreada ABCD muestra el área adecuada del LPP dado.
Se puede ver que el área adecuada está delimitada.
Las coordenadas de los puntos de esquina del área adecuada son A(2, 13), B(2, 0), C(4, 12) y D(8, 0).
Los valores de la función objetivo, Z en estos puntos de esquina se dan en la siguiente tabla:
Punto de esquina
Valor de la Función Objetivo Z = 20 x + 10 y
A(2, 13)
Z = 20 × 2 + 10 × 13 = 170
B(2, 0)
Z = 20 × 2 + 10 × 0 = 40
C(8, 0)
Z = 20 × 8 + 10 × 0 = 160
D(4, 12)
Z = 20 × 4 + 10 × 12 = 200
Como se puede ver en la tabla, Z es máximo en x = 4 e y = 12 y el valor máximo de Z es 200.
Por lo tanto,
El valor máximo de Z es 200.
Pregunta 28: Resuelva gráficamente el siguiente problema de programación lineal:
Minimizar z= 6x + 3y
Sujeto a las restricciones:
4x + y ≥ 80
x + 5y ≥ 115
3x + 2y ≤ 150
x ≥ 0, y ≥ 0
Solución:
Aquí las restricciones dadas son
4x + y ≥ 80
x + 5y ≥ 115
3x + 2y ≤ 150
x, y ≥ 0Convirtiendo lo dado en ecuaciones en ecuaciones,
Obtendremos
4x + y = 80, x + 5y = 115, 3x + 2y = 150, x = 0 y y = 0
Estas líneas se dibujan en el gráfico y el área sombreada ABC representa el área adecuada del LPP dado.
Se puede ver que el área adecuada está delimitada.
Las coordenadas de los vértices del adecuado son A(2, 72), B(15, 20) y C(40, 15).
Los valores de la función objetivo, Z en estos puntos de esquina se dan en la siguiente tabla:
Punto de esquina
Valor de la Función Objetivo Z = 6 x + 3 y
A(2, 72)
Z = 6 × 2 + 3 × 72 = 228
b(15, 20)
Z = 6 × 15 + 3 × 20 = 150
C(40, 15)
Z = 6 × 40 + 3 × 15 = 285
Como se ve en la tabla, Z es mínimo en x = 15 e y = 20 y el valor mínimo de Z es 150.
Por lo tanto,
El valor mínimo de Z es 150.
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA







