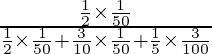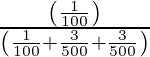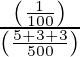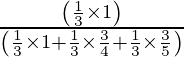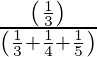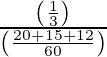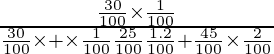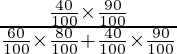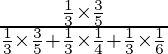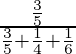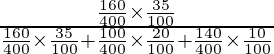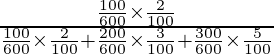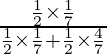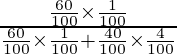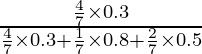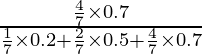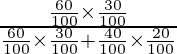Clase 12 RD Sharma Solutions – Capítulo 31 Probabilidad – Ejercicio 31.7

Pregunta 14. Tres máquinas A, B y C fabrican un artículo. Del número total de artículos fabricados durante un período específico, el 50 % se fabrica en la máquina A, el 30 % en la máquina A, el 20 % en la C. El 2 % de los artículos producidos en A y el 2% de los artículos producidos en B son defectuosos y el 3% de estos producidos en C son defectuosos. Todos los elementos se almacenan a la vez. Se extrae un artículo al azar y se encuentra defectuoso. ¿Cuál es la probabilidad de que haya sido fabricado en la máquina A?

Solución:

Supongamos que E sea el evento de obtener un artículo defectuoso.

Entonces tenemos

P(A) = 50 % = 1/2

P(B) = 30 % = 3/10

P(C) = 20 % = 1/5

También tenemos,

P(E/A) = 2 % = 1/50

P(E/B) = 2 % = 1/50

P(E/C) = 3 % = 3/100

Ahora,

P(el artículo defectuoso sacado fue fabricado en la máquina A) = $\frac{P\left( A \right) \times P\left( E/A \right)}{P\left( A \right) \times P\left( E/A \right) + P\left( B \right) \times P\left( E/B \right) + P\left( C \right) \times P\left( E/C \right)}$

= $\frac{\frac{1}{2} \times \frac{1}{50}}{\frac{1}{2} \times \frac{1}{50} + \frac{3}{10} \times \frac{1}{50} + \frac{1}{5} \times \frac{3}{100}}$

= $\frac{\left( \frac{1}{100} \right)}{\left( \frac{1}{100} + \frac{3}{500} + \frac{3}{500} \right)}$

= $\frac{\left( \frac{1}{100} \right)}{\left( \frac{5 + 3 + 3}{500} \right)}$

= $\frac{\frac{1}{100}}{\frac{11}{500}}$

= 500/1100

= 5/11

Pregunta 15. Hay tres monedas. Una es una moneda de dos caras (que tiene cara en ambas caras), otra es una moneda sesgada que sale cara el 75 % de las veces y la tercera también es una moneda sesgada que sale cruz el 40 % de las veces. Se elige una de las tres monedas al azar y se lanza al aire, y sale cara. ¿Cuál es la probabilidad de que fuera la moneda de dos caras?

Solución:

Supongamos

A = el evento de elegir una moneda de dos caras,

B = el evento de elegir una moneda sesgada que sale cara el 75 % de las veces

C = el evento de elegir una moneda sesgada que sale cruz el 40 % de las veces

E = el evento de sacar cara.

Ahora,

P(A) = 1/3

P(B) = 1/3

P(B) = 1/3

También tenemos,

P(E/A) = 1

P(E/B) = 75 % = 75/100 = 3/4

P(E/C) = 60 % = 60/100 = 3/5

Usando el teorema de Bayes, la probabilidad requerida es

P(la cara mostrada era de una moneda de dos caras) = P (A/E)

= $\frac{P\left( A \right) \times P\left( E/A \right)}{P\left( A \right) \times P\left( E/A \right) + P\left( B \right) \times P\left( E/B \right) + P\left( C \right) \times P\left( E/C \right)}$

= $\frac{\left( \frac{1}{3} \times 1 \right)}{\left( \frac{1}{3} \times 1 + \frac{1}{3} \times \frac{3}{4} + \frac{1}{3} \times \frac{3}{5} \right)}$

= $\frac{\left( \frac{1}{3} \right)}{\left( \frac{1}{3} + \frac{1}{4} + \frac{1}{5} \right)}$

= $\frac{\left( \frac{1}{3} \right)}{\left( \frac{20 + 15 + 12}{60} \right)}$

= $\frac{\left( \frac{1}{3} \right)}{\left( \frac{47}{60} \right)}$

= 20/47

Pregunta 16. En una fábrica, una máquina A produce el 30% de la producción total, la máquina B produce el 25% y la máquina C produce la producción restante. Si los artículos defectuosos producidos por las máquinas A, B y C son 1%, 1.2%, 2% respectivamente. Tres máquinas trabajando juntas producen 10000 artículos en un día. Se extrae un artículo al azar de la producción de un día y se encuentra defectuoso. ¿Encuentre la probabilidad de que haya sido producido por la máquina B?

Solución:

Supongamos que los eventos son

A = el artículo es defectuoso

E ₁ = se elige la máquina A

E ₂ = se elige la máquina B

E ₃ = se elige la máquina C

Asi que,

P(E1 ) = _30/100

P(E2 ₎ = 25/100

P( E3) = _45/100

Ahora,

P(A/E ₁ ) = 1/100

P(A/E ₂ ) = 1,2/1000

P(A/E ₃ ) = 2/100

Usando el teorema de Bayes, la probabilidad requerida es

P(E ₁ /A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{30}{100} \times \frac{1}{100}}{\frac{30}{100} \times + \times \frac{1}{100}\frac{25}{100}\frac{1 . 2}{100} + \frac{45}{100} \times \frac{2}{100}}$

= $\frac{30}{30 + 30 + 90}$

= 30/150

= 1/5

= 0,2

Pregunta 17. Una empresa tiene dos plantas para fabricar bicicletas. La primera planta fabrica el 60% de las bicicletas y la segunda planta el 40%. Del 80% de las bicicletas son calificadas de calidad estándar en la primera planta y el 90% de calidad estándar en la segunda planta. Se toma una bicicleta al azar y se encuentra que es de calidad estándar. Halla la probabilidad de que provenga de la segunda planta.

Solución:

Supongamos que los eventos son

A = el ciclo es de calidad estándar

E ₁ = se elige la planta I

E ₂ = se elige la planta II.

Asi que,

P(E1 ) = _60/100

P(E2 ₎ = 40/100

Ahora,

P(A/E ₁ ) = 80/100

P(A/E ₂ ) = 90/100

Usando el teorema de Bayes, la probabilidad requerida es

P(E2 /A) ₌ $\frac{P\left( E_2 \right)P\left( A/ E_2 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{40}{100} \times \frac{90}{100}}{\frac{60}{100} \times \frac{80}{100} + \frac{40}{100} \times \frac{90}{100}}$

= $\frac{36}{48 + 36}$

= 36/84

= 3/7

Pregunta 18. Tres urnas A, B y C contienen 6 rojas y 4 blancas; 2 rojos y 6 blancos; y 1 bola roja y 5 blancas respectivamente. Se elige una urna al azar y se extrae una bola. Si se encuentra que la bola extraída es roja, encuentre la probabilidad de que la bola haya sido extraída de la urna A.

Solución:

Supongamos que los eventos son

A = la pelota es roja

E ₁ = se elige la urna A

E ₂ = se elige la urna B

E ₂ = se elige la urna C.

Entonces, P(E ₁ ) = 1/3

P(E2 ₎ = 1/3

P(E3 ₎ = 1/3

Ahora,

P(A/E ₁ ) = 6/10 = 3/5

P(A/E ₂ ) = 2/8 = 1/4

P(A/E ₃ ) = 1/6

Usando el teorema de Bayes, la probabilidad requerida es

P(E ₁ /A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{1}{3} \times \frac{3}{5}}{\frac{1}{3} \times \frac{3}{5} + \frac{1}{3} \times \frac{1}{4} + \frac{1}{3} \times \frac{1}{6}}$

= $\frac{\frac{3}{5}}{\frac{3}{5} + \frac{1}{4} + \frac{1}{6}}$

= 36/61

Pregunta 19. De un grupo de 400 personas, 160 son fumadores y no vegetarianos, 100 son fumadores y vegetarianos y el resto son no fumadores y vegetarianos. Las probabilidades de contraer una enfermedad especial del pecho son del 35 %, 20 % y 10 % respectivamente. Se elige una persona del grupo al azar y se descubre que padece la enfermedad. ¿Cuál es la probabilidad de que la persona seleccionada sea fumadora y no vegetariana?

Solución:

Supongamos que los eventos son

A = la persona padece la enfermedad

E ₁ = fumador y no vegetariano

E ₂ = fumador y vegetariano

E ₃ = no fumador y vegetariano

Entonces, P(E ₁ ) = 160/400

P(E2 ₎ = 100/400

P( E3) = _140/400

Ahora,

P(A/E ₁ ) = 35/100

P(A/E ₂ ) = 20/100

P(A/E ₃ ) = 10/100

Usando el teorema de Bayes, la probabilidad requerida es

P(E ₁ /A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{160}{400} \times \frac{35}{100}}{\frac{160}{400} \times \frac{35}{100} + \frac{100}{400} \times \frac{20}{100} + \frac{140}{400} \times \frac{10}{100}}$

= $\frac{560}{560 + 200 + 140}$

= 560/900

= 28/45

Pregunta 20. Una fábrica tiene tres máquinas A, B y C, que producen diariamente 100, 200 y 300 artículos de un tipo particular. Las máquinas producen 2%, 3% y 5% de artículos defectuosos respectivamente. Un día, cuando terminó la producción, se recogió un artículo al azar y se descubrió que estaba defectuoso. Encuentre la probabilidad de que haya sido producido por la máquina A.

Solución:

Supongamos que los eventos son

A = el artículo es defectuoso

E ₁ = se elige la máquina A

E ₂ = se elige la máquina B

E ₃ = se elige la máquina C

Entonces, P(E ₁ ) = 100/600

P(E2 ₎ = 200/600

P( E3) = _300/600

Ahora,

P(A/E ₁ ) = 2/100

P(A/E ₂ ) = 3/100

P(A/E ₃ ) = 5/100

Usando el teorema de Bayes, la probabilidad requerida es

P(E ₁ /A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{100}{600} \times \frac{2}{100}}{\frac{100}{600} \times \frac{2}{100} + \frac{200}{600} \times \frac{3}{100} + \frac{300}{600} \times \frac{5}{100}}$

= $\frac{2}{2 + 6 + 15}$

= 2/23

Pregunta 21. Una bolsa contiene 1 pelota blanca y 6 rojas, y una segunda bolsa contiene 4 pelotas blancas y 3 rojas. Se toma una de las bolsas al azar y se extrae una bola al azar y se encuentra que es de color blanco. Calcula la probabilidad de que la bola extraída fuera de la primera bolsa.

Solución:

Supongamos que los eventos son

A = la pelota es blanca

E ₁ = se elige la bolsa I

E ₂ = se elige la bolsa II

Entonces, P(E ₁ ) = 1/2

P(E ₂ ) = 1/2

Ahora,

P(A/E ₁ ) = 1/7

P(A/E ₂ ) = 4/7

Usando el teorema de Bayes, la probabilidad requerida es

P(E ₁ /A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{\frac{1}{2} \times \frac{1}{7}}{\frac{1}{2} \times \frac{1}{7} + \frac{1}{2} \times \frac{4}{7}}$

= $\frac{1}{1 + 4}$

= 1/5

Pregunta 22. En cierta universidad, el 4% de los niños y el 1% de las niñas miden más de 1,75 metros. Además, el 60% de los estudiantes de las universidades son niñas. Se encuentra que un estudiante seleccionado al azar de la universidad mide más de 1.75 metros. Encuentre la probabilidad de que el estudiante seleccionado sea una niña.

Solución:

Supongamos que los eventos son

A = La altura del alumno es mayor a 1.75 m

E ₁ = El estudiante seleccionado es una niña

E ₂ = El estudiante seleccionado es un niño

Asi que,

P(E1 ) = _60/100

P(E2 ₎ = 40/100

Ahora,

P(A/E ₁ ) = 1/100

P(A/E ₁ ) = 4/100

Usando el teorema de Bayes, la probabilidad requerida es

P(E ₁ /A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{\frac{60}{100} \times \frac{1}{100}}{\frac{60}{100} \times \frac{1}{100} + \frac{40}{100} \times \frac{4}{100}}$

= $\frac{6}{6 + 16}$

= 6/22

= 3/11

Pregunta 23. Para A, B y C, las posibilidades de ser seleccionado como gerente de una empresa están en la proporción 4:1:2 respectivamente. Las probabilidades respectivas de que introduzcan un cambio radical en la estrategia de marketing son 0,3, 0,8 y 0,5. Si se produce el cambio, encuentre la probabilidad de que se deba al nombramiento de B o C.

Solución:

Supongamos que los eventos son

A = El cambio se lleva a cabo

E ₁ = Se selecciona A

E ₂ = B está seleccionado

E ₃ = C está seleccionado

Asi que,

P(E1 ₎ = 4/7

P(E2 ₎ = 1/7

P(E3 ₎ = 2/7

Ahora,

P(A/E1 ₎ = 0,3

P(A/E ₂ ) = 0,8

P(A/E3 ₎ = 0,5

Usando el teorema de Bayes, la probabilidad requerida es

P(E ₁ /A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{4}{7} \times 0 . 3}{\frac{4}{7} \times 0 . 3 + \frac{1}{7} \times 0 . 8 + \frac{2}{7} \times 0 . 5}$

= $\frac{1 . 2}{1 . 2 + 0 . 8 + 1}$

= 1,2/3

= 2/5

1 – P(E ₁ /A) = 1 – 2/5 = 3/5

Pregunta 24. Tres personas A, B y C solicitan un puesto de Gerente en una Empresa Privada. Las posibilidades de su selección (A, B y C) están en la relación 1 : 2 : 4. Las probabilidades de que A, B y C puedan introducir cambios para mejorar las utilidades de la empresa son 0.8, 0.5 y 0.3, respectivamente. . Si el cambio no ocurre, encuentre la probabilidad de que se deba al nombramiento de C.

Solución:

Supongamos que los eventos son

E ₁ = La selección de A como gerente

E ₂ = La selección de B como gerente

E ₃ = La selección de C como gerente

Asi que,

P(E ₁ ) = La probabilidad de selección de A = 1/7

P(E ₂ ) = La probabilidad de selección de B = 2/7

P(E ₃ ) = La probabilidad de selección de C = 4/7

Supongamos que A es el evento que representa el cambio que no tiene lugar.

P(A/E ₁ ) = Probabilidad de que A no introduzca cambio = 0.2

P(A/E ₂ ) = Probabilidad de que B no introduzca cambio = 0.5

P(A/E ₃ ) = Probabilidad de que C no introduzca cambio = 0.7

Entonces, la probabilidad requerida = P(A/E ₃ )

Usando el teorema de Bayes, la probabilidad requerida es

P(A/E ₃ ) = $\frac{P\left( E_3 \right)P\left( A/ E_3 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{4}{7} \times 0 . 7}{\frac{1}{7} \times 0 . 2 + \frac{2}{7} \times 0 . 5 + \frac{4}{7} \times 0 . 7}$

= $\frac{2 . 8}{0 . 2 + 1 + 2 . 8}$

= 2,8/4

= 0,7

Pregunta 25. Una compañía de seguros aseguró 2000 scooters y 3000 motocicletas. La probabilidad de un accidente con un scooter es 0,01 y la de una motocicleta es 0,02. Un vehículo asegurado tuvo un accidente. Encuentre la probabilidad de que el vehículo del accidente fuera una motocicleta.

Solución:

Supongamos que los eventos son

A = El vehículo se encuentra con el accidente

E ₁ = es un scooter

E ₂ = es una motocicleta

Asi que,

P(E1 ) = _2000/5000 = 0,4

P(E2 ₎ = 3000/5000 = 0,6

Ahora,

P(A/E1 ₎ = 0,01

P(A/E2 ₎ = 0,02

Usando el teorema de Bayes, la probabilidad requerida es

P(E2 /A) ₌ $\frac{P\left( E_2 \right)P\left( A/ E_2 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{0 . 6 \times 0 . 02}{0 . 6 \times 0 . 02 + 0 . 4 \times 0 . 01}$

= $\frac{0 . 012}{0 . 012 + 0 . 004}$

= 0,012/0,016

= 3/4

Pregunta 26. De los estudiantes de una universidad, se sabe que el 60% reside en un albergue y el 40% no reside en un albergue. Los resultados del año anterior informan que el 30 % de los estudiantes que residen en albergue obtienen una calificación A y el 20 % de los que no residen en albergue obtienen una calificación A en su examen anual. Al final del año, se elige al azar un estudiante de la universidad y tiene una calificación de A. ¿Cuál es la probabilidad de que el alumno seleccionado sea hostelero?

Solución:

Supongamos que los eventos son

A = El alumno seleccionado obtiene la nota A

E ₁ = reside en un albergue

E ₂ = no reside en un albergue

Entonces, P(E ₁ ) = 60/100

P(E2 ₎ = 40/100

Ahora,

P(A/E ₁ ) = 30/100

P(A/E ₂ ) = 20/100

Usando el teorema de Bayes, la probabilidad requerida es

P(E ₁ /A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{\frac{60}{100} \times \frac{30}{100}}{\frac{60}{100} \times \frac{30}{100} + \frac{40}{100} \times \frac{20}{100}}$

= $\frac{18}{18 + 8}$

= 9/13

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 RD Sharma Solutions – Capítulo 31 Probabilidad – Ejercicio 31.7 | conjunto 2

Pregunta 18. Tres urnas A, B y C contienen 6 rojas y 4 blancas; 2 rojos y 6 blancos; y 1 bola roja y 5 blancas respectivamente. Se elige una urna al azar y se extrae una bola. Si se encuentra que la bola extraída es roja, encuentre la probabilidad de que la bola haya sido extraída de la urna A.

Pregunta 21. Una bolsa contiene 1 pelota blanca y 6 rojas, y una segunda bolsa contiene 4 pelotas blancas y 3 rojas. Se toma una de las bolsas al azar y se extrae una bola al azar y se encuentra que es de color blanco. Calcula la probabilidad de que la bola extraída fuera de la primera bolsa.

Pregunta 25. Una compañía de seguros aseguró 2000 scooters y 3000 motocicletas. La probabilidad de un accidente con un scooter es 0,01 y la de una motocicleta es 0,02. Un vehículo asegurado tuvo un accidente. Encuentre la probabilidad de que el vehículo del accidente fuera una motocicleta.

Deja una respuesta Cancelar la respuesta