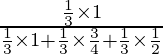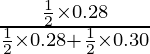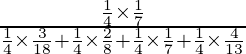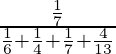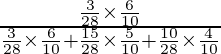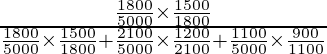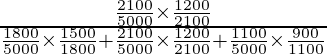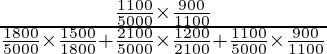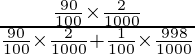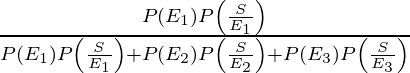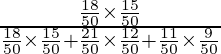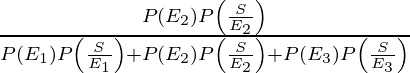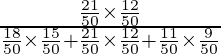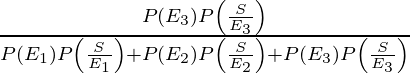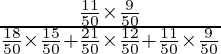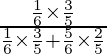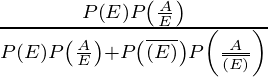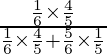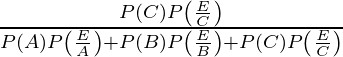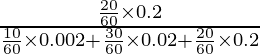Clase 12 RD Sharma Solutions – Capítulo 31 Probabilidad – Ejercicio 31.7 | conjunto 3

Posted on by Rudeus Greyrat

Pregunta 27. Hay tres monedas. Una es una moneda de dos caras, otra es una moneda sesgada que sale cara el 75% de las veces y la tercera es una moneda imparcial. Se elige una de las tres monedas al azar y se lanza al aire, muestra cara. ¿Cuál es la probabilidad de que fuera la moneda de dos caras?

Solución:

Supongamos que los eventos son

E 1 = elegir una moneda de dos caras

E 2 = elegir una moneda sesgada 

E 3 = elegir una moneda imparcial

A = la moneda muestra cara.

Asi que, 

P(E1 ) = 1/3

P(E2 ) = 1/3

P(E3 ) = 1/3

Ahora,

P(A/E 1 ) = 1

P(A/E 2 ) = 75% = 3/4

P(A/E 3 ) = 1/2

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{1}{3} \times 1}{\frac{1}{3} \times 1 + \frac{1}{3} \times \frac{3}{4} + \frac{1}{3} \times \frac{1}{2}}

= 4/9

Pregunta 28. Suponga que la probabilidad de que un paciente sufra un infarto es del 40%. También se supone que el curso de meditación y yoga reduce el riesgo de ataque cardíaco en un 30% y la prescripción de ciertos medicamentos reduce sus posibilidades en un 25%. A la vez un paciente puede elegir cualquiera de las dos opciones con iguales probabilidades. Se da que luego de pasar por una de las dos opciones y el paciente seleccionado al azar sufre un infarto. Encuentre la probabilidad de que el paciente haya seguido un curso de meditación y yoga.

Solución:

Supongamos que los eventos son

E 1 = seguir el curso de yoga y meditación

E 2 = seguir las prescripciones de medicamentos

A = la persona seleccionada tuvo un ataque al corazón

Asi que, 

P(E1 ) = 1/2

P(E 2 ) = 1/2

Ahora,

P(A/E1 ) = 0,4 x 0,70 = 0,28

P(A/E 2 ) = 0,4 x 0,75 = 0,30

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{1}{2} \times 0.28}{\frac{1}{2} \times 0.28 + \frac{1}{2} \times 0.30}

= 14/29

Pregunta 29. Las bolas de colores se distribuyen en cuatro cajas como se muestra en la siguiente tabla:

Caja

Color

 

Negro

Blanco

Rojo

Azul

yo

3

4

5

6

Yo

2

2

2

2

tercero

1

2

3

1

IV

4

3

1

5

Se selecciona una caja al azar y luego se extrae una bola al azar de la caja seleccionada. El color de la bola es negro, cual es la probabilidad de que la bola extraída sea de la caja III.

Solución:

Supongamos que los eventos son

A = la pelota es negra

E 1 = caja que seleccioné

E 2 = casilla II seleccionada

E 3 = se selecciona la casilla III 

E 4 = se selecciona la casilla IV

Asi que, 

P(E1 ) = 1/4

P(E2) = 1/4

P(E3 ) = 1/4

P(E4 ) = 1/4

Ahora,

P(A/E 1 ) = 3/18

P(A/E 2 ) = 2/8

P(A/E 3 ) = 1/7

P(A/E4 ) = 4/13

P(E 3 /A) = \frac{P\left( E_3 \right)P\left( A/ E_3 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)+P\left( E_3 \right)P\left( A/ E_3 \right)+P\left( E_4 \right)P\left( A/ E_4 \right)}

= \frac{\frac{1}{4} \times \frac{1}{7}}{\frac{1}{4} \times \frac{3}{18} + \frac{1}{4} \times \frac{2}{8} + \frac{1}{4} \times \frac{1}{7} + \frac{1}{4} \times \frac{4}{13}}

= \frac{\frac{1}{7}}{\frac{1}{6} + \frac{1}{4} + \frac{1}{7} + \frac{4}{13}}

= 156/947

Pregunta 30. Si una máquina está configurada correctamente, produce un 90 % de artículos aceptables. Si está configurado incorrectamente, produce solo un 40% de artículos aceptables. La experiencia pasada muestra que el 80% de las configuraciones se realizan correctamente. Si después de cierta configuración, la máquina produce 2 artículos aceptables, encuentre la probabilidad de que la máquina esté configurada correctamente.

Solución:

Supongamos que los eventos son

A = la máquina produce dos artículos aceptables.

E 1 = la máquina está configurada correctamente 

E 2 = la máquina está mal configurada

Asi que, 

P(E1 ) = 0,8

P(E2 ) = 0,2

Ahora,

P(A/E1 ) = 0,9 (0,9) = 0,81

P(A/E 2 ) = 0,40 (0,40) = 0,16

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{0 . 8 \times 0 . 81}{0 . 8 \times 0 . 81 + 0 . 2 \times 0 . 16}

= 81/85

Pregunta 31. La bolsa A contiene 3 bolas rojas y 5 negras, mientras que la bolsa B contiene 4 bolas rojas y 4 negras. Se transfieren dos bolas al azar de la bolsa A a la bolsa B y luego se extrae una bola de la bolsa B al azar. Si se encuentra que la bola extraída de la bolsa B es roja, calcule la probabilidad de que se hayan transferido dos bolas rojas de A a B.

Solución:

Según la pregunta, la bolsa A contiene 3 bolas rojas y 5 negras y la bolsa B contiene 4 bolas rojas y 4 negras.

Supongamos que los eventos son

E 1 = Dos bolas rojas se transfieren de la bolsa A a la bolsa B.

E 2 = Una bola roja y una bola negra se transfieren de la bolsa A a la bolsa B.

E 3 = Dos bolas negras se transfieren de la bolsa A a la bolsa B.

A = La bola extraída de la bolsa B es roja.

Asi que,

P(E1 ) =  = 3/28\frac{{^3}{}{C}_2}{{^8}{}{C}_2}

P(E 2 ) =  \frac{{^3}{}{C}_1 \times {^5}{}{C}_1}{^{8}{}{C}_2} = 15/28

P(E 3 ) =  \frac{^{5}{}{C}_2}{^{8}{}{C}_2} = 10/28

También,

P(A/E 1 ) = 6/10

P(A/E 2 ) = 5/10

P(A/E 3 ) = 4/10

P(E 1 /A) es la probabilidad requerida de que dos bolas rojas fueran transferidas de A a B dado que la bola extraída de la bolsa B es roja  

= \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)+P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{3}{28} \times \frac{6}{10}}{\frac{3}{28} \times \frac{6}{10} + \frac{15}{28} \times \frac{5}{10} + \frac{10}{28} \times \frac{4}{10}}

= \frac{18}{18 + 75 + 40}

= 18/133

Pregunta 32. Sean d 1 , d 2 , d 3 tres enfermedades mutuamente excluyentes. Sea S el conjunto de síntomas observables de estas enfermedades. Un médico tiene la siguiente información de una muestra aleatoria de 5000 pacientes: 1800 tenían la enfermedad d 1 , 2100 tenían la enfermedad d 2 y los demás tenían la enfermedad d 3 . 1500 pacientes con enfermedad d 1 , 1200 pacientes con enfermedad d 2 y 900 pacientes con enfermedad d 3 mostraron los síntomas. ¿Cuál de las enfermedades es más probable que tenga el paciente?

Solución:

Supongamos que los eventos son

A = el paciente muestra síntomas S

E 1 = tiene enfermedad d 1

E 2 = tiene enfermedad​ d 2

E 3 = tiene enfermedad​ d 3

Asi que, 

P(E1 ) = 1800/5000

P(E2 ) = 2100/5000

P( E3) = 1100/5000

Ahora,

P(A/E 1 ) =1500/1800

P(A/E 2 ) = 1200/2100

P(A/E 3 ) = 900/1100

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{1800}{5000} \times \frac{1500}{1800}}{\frac{1800}{5000} \times \frac{1500}{1800} + \frac{2100}{5000} \times \frac{1200}{2100} + \frac{1100}{5000} \times \frac{900}{1100}}

= \frac{15}{15 + 12 + 9}

= 15/36

= 5/12

P(E2 /A)  =\frac{P\left( E_2 \right)P\left( A/ E_2 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{2100}{5000} \times \frac{1200}{2100}}{\frac{1800}{5000} \times \frac{1500}{1800} + \frac{2100}{5000} \times \frac{1200}{2100} + \frac{1100}{5000} \times \frac{900}{1100}}

= \frac{12}{15 + 12 + 9}

= 12/36

= 1/3

P(E 3 /A) = \frac{P\left( E_3 \right)P\left( A/ E_3 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{1100}{5000} \times \frac{900}{1100}}{\frac{1800}{5000} \times \frac{1500}{1800} + \frac{2100}{5000} \times \frac{1200}{2100} + \frac{1100}{5000} \times \frac{900}{1100}}

= \frac{9}{15 + 12 + 9}

= 9/36

= 1/4

Como P(E 1 /A ) es máximo, lo más probable es que la persona tenga la enfermedad d 1 .

Pregunta 33. Una prueba para la detección de una determinada enfermedad no es infalible. La prueba detectará correctamente la enfermedad el 90 % de las veces, pero detectará incorrectamente la enfermedad el 1 % de las veces. Para una gran población de la cual se estima que el 0,2% tiene la enfermedad, se selecciona una persona al azar, se le hace la prueba y se le dice que tiene la enfermedad. ¿Cuáles son las posibilidades de que la persona realmente tenga la enfermedad?

Solución:

Supongamos que los eventos son

A = la persona padece la enfermedad

E 1 = la prueba detecta la enfermedad correctamente 

E 2 = la prueba no detecta correctamente la enfermedad

Asi que, 

P(E1 ) = 90/100

P(E2 ) = 1/100

Ahora,

P(A/E 1 ) = 2/1000

P(A/E 2 ) = 998/1000

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{90}{100} \times \frac{2}{1000}}{\frac{90}{100} \times \frac{2}{1000} + \frac{1}{100} \times \frac{998}{1000}}

= \frac{180}{180 + 998}

= 180/1178

= 90/589

Pregunta 34. Sean d 1 , d 2 , d 3 , d 4 tres enfermedades mutuamente excluyentes. Sea S el conjunto de síntomas observables de estas enfermedades. Un médico tiene la siguiente información de una muestra aleatoria de 5000 pacientes: 1800 tenían la enfermedad d 1 , 2100 tenían la enfermedad d 2 y otros tenían la enfermedad d 3 . 1500 pacientes con enfermedad d 1 , 1200 pacientes con enfermedad d 2 y 900 pacientes con enfermedad d 3 mostraron los síntomas. ¿Cuál de las enfermedades es más probable que tenga el paciente?

Solución:

Supongamos que los eventos son

E 1 = El paciente tenía enfermedad d 1

E 2 = El paciente tenía enfermedad d 2

E 3 = El paciente tenía enfermedad d 3

S = El paciente mostró el síntoma

Además, E 1 , E 2 y E 3 son eventos mutuamente excluyentes y exhaustivos.

Asi que, 

P(E1 ) = 1800/1500 = 18/50

P(E 2 ) = 2100/5000 = 21/50

P(E 3 ) = 1100/5000 = 11/50

Ahora,  

P(S/E 1 ) = La probabilidad de que el paciente tuviera la enfermedad d 1 y mostrara síntomas S = 1500/5000 = 15/50

P(S/E 2 ) = La probabilidad de que el paciente tuviera la enfermedad d 2 y mostrara síntomas S = 1200/5000 = 12/50

P(S/E 3 ) = La probabilidad de que el paciente tuviera la enfermedad d 3 y mostrara síntomas S = 900/5000 = 9/50

P(E 1 /S) es la probabilidad de que el paciente tuviera la enfermedad d 1 tal que aparezcan los síntomas de d 1

= \frac{P\left( E_1 \right)P\left( \frac{S}{E_1} \right)}{P\left( E_1 \right)P\left( \frac{S}{E_1} \right) + P\left( E_2 \right)P\left( \frac{S}{E_2} \right) + P\left( E_3 \right)P\left( \frac{S}{E_3} \right)}

= \frac{\frac{18}{50} \times \frac{15}{50}}{\frac{18}{50} \times \frac{15}{50} + \frac{21}{50} \times \frac{12}{50} + \frac{11}{50} \times \frac{9}{50}}

= 270/621

P(E 2 /S) es la probabilidad de que el paciente tuviera la enfermedad d 2 tal que aparezca el síntoma de d 2

= \frac{P\left( E_2 \right)P\left( \frac{S}{E_2} \right)}{P\left( E_1 \right)P\left( \frac{S}{E_1} \right) + P\left( E_2 \right)P\left( \frac{S}{E_2} \right) + P\left( E_3 \right)P\left( \frac{S}{E_3} \right)}

= \frac{\frac{21}{50} \times \frac{12}{50}}{\frac{18}{50} \times \frac{15}{50} + \frac{21}{50} \times \frac{12}{50} + \frac{11}{50} \times \frac{9}{50}}

= 252/621

P(E 3 /S) es la probabilidad de que el paciente tuviera la enfermedad d 3 tal que aparezca el síntoma de d 3

= \frac{P\left( E_3 \right)P\left( \frac{S}{E_3} \right)}{P\left( E_1 \right)P\left( \frac{S}{E_1} \right) + P\left( E_2 \right)P\left( \frac{S}{E_2} \right) + P\left( E_3 \right)P\left( \frac{S}{E_3} \right)}

= \frac{\frac{11}{50} \times \frac{9}{50}}{\frac{18}{50} \times \frac{15}{50} + \frac{21}{50} \times \frac{12}{50} + \frac{11}{50} \times \frac{9}{50}}

= 99/621

Por lo tanto, P(E 1 /A) es el máximo, entonces es más probable que el paciente tenga la enfermedad d 1 .

Pregunta 35. Se sabe que A dice la verdad 3 de cada 5 veces. Lanza un dado e informa que es uno. Encuentre la probabilidad de que en realidad sea uno.

Solución:

Supongamos que los eventos son

A = el hombre informa la aparición de 1 al lanzar un dado

E 1 = 1 ocurre 

E 2 = 1 no ocurre

Asi que, 

P(E1 ) = 1/6

P(E2 ) = 5/6

Ahora,

P(A/E 1 ) = 3/5

P(A/E 2 ) = 2/5

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{1}{6} \times \frac{3}{5}}{\frac{1}{6} \times \frac{3}{5} + \frac{5}{6} \times \frac{2}{5}}

= \frac{3}{3 + 10}

= 3/13

Pregunta 36. A dice la verdad 8 de cada 10 veces. Se lanza un dado. Él informa que fueron 5. ¿Cuál es la probabilidad de que en realidad fueran 5?

Solución:

Supongamos que A es el evento de que el hombre informa que 5 ocurre y E el evento de que 5 realmente aparece.

Asi que, 

P(E) = 1/6

P(\overline{E})  = 1 – 1/6 = 5/6

También,  

P(A/E) = Probabilidad de que el hombre informe que 5 ocurre dado que 5 realmente aparece 

= Probabilidad de que el hombre diga la verdad 

= 8/10

= 4/5

P\left(A/\overline{E}\right) = Probabilidad de que el hombre informe que 5 ocurra dado que 5 no aparece 

= Probabilidad de que el hombre no diga la verdad 

= 1 – 4/5

= 1/5

Por lo tanto, la probabilidad requerida = P(E/A)

= \frac{P\left( E \right)P\left( \frac{A}{E} \right)}{P\left( E \right)P\left( \frac{A}{E} \right) + P\left(\overline{ (E) } \right)P\left( \frac{A}{\overline{(E)}} \right)}

= \frac{\frac{1}{6} \times \frac{4}{5}}{\frac{1}{6} \times \frac{4}{5} + \frac{5}{6} \times \frac{1}{5}}

= 4/9

Pregunta 37. Al responder una pregunta en una prueba de opción múltiple, un estudiante sabe la respuesta o la adivina. Sea 3/4 la probabilidad de que sepa la respuesta y 1/4 la probabilidad de que adivine. Suponiendo que un estudiante que adivina la respuesta acertará con una probabilidad de 1/4. ¿Cuál es la probabilidad de que un estudiante sepa la respuesta dado que la contestó correctamente?

Solución:

Supongamos que los eventos son

A = la respuesta es correcta

E 1 = el estudiante sabe la respuesta

E 2 = el alumno adivina la respuesta

Asi que, 

P(E1 ) = 3/4

P(E 2 ) = 1/4

Ahora, 

P(A/E 1 ) = 1

P(A/E 2 ) = 1/4

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{3}{4} \times 1}{\frac{3}{4} \times 1 + \frac{1}{4} \times \frac{1}{4}}

= 3/3 + 1/4

= 12/13

Pregunta 38. Un análisis de sangre de laboratorio tiene una eficacia del 99% para detectar una determinada enfermedad cuando su infección está presente. Sin embargo, la prueba también arroja un resultado falso positivo para el 0,5% de las personas sanas analizadas (es decir, si se realiza la prueba a una persona sana, entonces, con una probabilidad de 0,005, la prueba implicará que tiene la enfermedad). Si el 0,1% de la población en realidad tiene la enfermedad, ¿cuál es la probabilidad de que una persona tenga la enfermedad dado que el resultado de su prueba es positivo?

Solución:

Supongamos que E 1 y E 2 son los eventos de que una persona tiene una enfermedad y una persona no tiene enfermedad.

Además, E 1 y E 2 son complementarios entre sí.

Entonces, P(E 1 ) + P(E 2 ) = 1

P(E1 ) = 0,001

=> PAGS (mi 2 ) = 1 − PAGS (mi 1 ) = 1 − 0.001 = 0.999

Supongamos que A es el evento de que el resultado del análisis de sangre sea positivo.

Ahora,

P(A/E 1 ) = 99% = 0,99

P(A/E 2 ) = 0,5 % = 0,005

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{0 . 001 \times 0 . 99}{0 . 001 \times 0 . 99 + 0 . 999 \times 0 . 005}

= 990/5985

= 22/133

Pregunta 39. Hay tres categorías de estudiantes en una clase de 60 estudiantes:

R: Muy trabajador; B: Regular pero no tan trabajador; C: 10 estudiantes descuidados e irregulares están en la categoría A, 30 en la categoría B y el resto en la categoría C. Se encuentra que la probabilidad de que los estudiantes de la categoría A no puedan obtener buenas notas en el examen del año final es 0.002, de categoría B es 0.02 y de categoría C, esta probabilidad es 0.20. Se encontró que un estudiante seleccionado al azar era uno que no podía sacar buenas notas en el examen. Encuentre la probabilidad de que este estudiante sea de categoría C.

Solución:

Supongamos que los eventos son

E = el alumno no pudo sacar buenas notas en el examen.

A = el estudiante es muy trabajador

B = el estudiante es regular pero no tan trabajador

C = el estudiante es descuidado e irregular

Aquí tenemos

PA(A) = 10/60

P(B) = 30/60

P(C) = 20/60

También,

P(E/A) = Probabilidad de que el alumno de categoría A no pueda sacar buenas notas en el examen = 0,002  

P(E/B) = Probabilidad de que un alumno de categoría B no pueda sacar buenas notas en el examen = 0,02

P(E/C) = Probabilidad de que un alumno de categoría C no pueda sacar buenas notas en el examen = 0,2

Entonces, P(C/E) es la probabilidad requerida 

= \frac{P\left( C \right)P\left( \frac{E}{C} \right)}{P\left( A \right)P\left( \frac{E}{A} \right) + P\left( B \right)P\left( \frac{E}{B} \right) + P\left( C \right)P\left( \frac{E}{C} \right)}

= \frac{\frac{20}{60} \times 0 . 2}{\frac{10}{60} \times 0 . 002 + \frac{30}{60} \times 0 . 02 + \frac{20}{60} \times 0 . 2}

= 4/4,62

= 400/462

= 200/231

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *