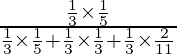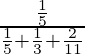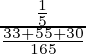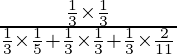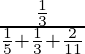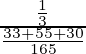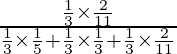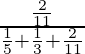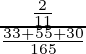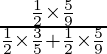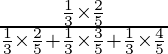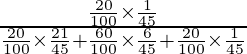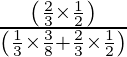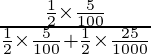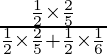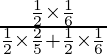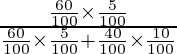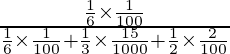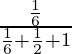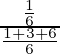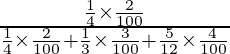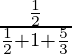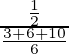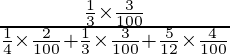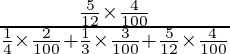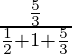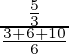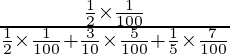Clase 12 RD Sharma Solutions – Capítulo 31 Probabilidad – Ejercicio 31.7 | Serie 1

Posted on by Rudeus Greyrat

Pregunta 1. El contenido de las urnas I, II, III es el siguiente:

Urna I: 1 bola blanca, 2 negras y 3 rojas

Urna II: 2 bolas blancas, 1 negra y 1 roja

Urna III: 4 bolas blancas, 5 negras y 3 rojas

Se elige una urna al azar y se extraen dos bolas. Resulta que son de color blanco y rojo. ¿Cuál es la probabilidad de que provengan de las Urnas I, II, III?

Solución:

Supongamos que E 1 , E 2 y E 3 son los eventos de seleccionar Urna I, Urna II y Urna III. Y también A ser el evento de que las dos bolas extraídas sean blancas y rojas.

Entonces, P(E 1 ) = 1/3

P(E2 ) = 1/3

P(E3 ) = 1/3

Ahora,

P(A/E 1 ) =  \frac{{}^1 C_1 \times^3 C_1}{{}^6 C_2} = 3/15 = 1/5

P(A/E 2 ) =  \frac{{}^2 C_1 \times^1 C_1}{{}^4 C_2} = 2/6 = 1/3

P(A/E 3 ) =  \frac{{}^4 C_1 \times^3 C_1}{{}^{12} C_2} = 12/66 = 2/11

Usando el teorema de Bayes, la probabilidad requerida es,

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{1}{3} \times \frac{1}{5}}{\frac{1}{3} \times \frac{1}{5} + \frac{1}{3} \times \frac{1}{3} + \frac{1}{3} \times \frac{2}{11}}

= \frac{\frac{1}{5}}{\frac{1}{5} + \frac{1}{3} + \frac{2}{11}}

= \frac{\frac{1}{5}}{\frac{33 + 55 + 30}{165}}

= 33/118

P(E2 /A)  =\frac{P\left( E_2 \right)P\left( A/ E_2 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{1}{3} \times \frac{1}{3}}{\frac{1}{3} \times \frac{1}{5} + \frac{1}{3} \times \frac{1}{3} + \frac{1}{3} \times \frac{2}{11}}

= \frac{\frac{1}{3}}{\frac{1}{5} + \frac{1}{3} + \frac{2}{11}}

= \frac{\frac{1}{3}}{\frac{33 + 55 + 30}{165}}

= 55/118

P(E 3 /A) = \frac{P\left( E_3 \right)P\left( A/ E_3 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{1}{3} \times \frac{2}{11}}{\frac{1}{3} \times \frac{1}{5} + \frac{1}{3} \times \frac{1}{3} + \frac{1}{3} \times \frac{2}{11}}

= \frac{\frac{2}{11}}{\frac{1}{5} + \frac{1}{3} + \frac{2}{11}}

= \frac{\frac{2}{11}}{\frac{33 + 55 + 30}{165}}

= 30/118

Pregunta 2. Una bolsa A contiene 2 bolas blancas y 3 rojas y una bolsa B contiene 4 bolas blancas y 5 rojas. Se extrae una bola al azar de una de las bolsas y se encuentra que es roja. Encuentre la probabilidad de que se haya sacado de la bolsa B.

Solución:

Supongamos que A, E 1 y E 2 son los eventos de que la pelota es roja, se elige la bolsa A y se elige la bolsa B.

Entonces, P(E 1 ) = 1/2

P(E 2 ) = 1/2

Ahora,

P(A/E 1 ) = 3/5

P(A/E 2 ) = 5/9

Usando el teorema de Bayes, la probabilidad requerida es,

P(E2 /A)  =\frac{P\left( E_2 \right)P\left( A/ E_2 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{1}{2} \times \frac{5}{9}}{\frac{1}{2} \times \frac{3}{5} + \frac{1}{2} \times \frac{5}{9}}

= 25/52

Pregunta 3. Tres urnas contienen 2 bolas blancas y 3 negras; 3 bolas blancas y 2 negras y 4 bolas blancas y 1 negra respectivamente. Se extrae una bola de una urna elegida al azar y se encuentra que es blanca. Encuentre la probabilidad de que se haya extraído de la primera urna.

Solución:

Consideremos E 1 , E 2 y E 3 como los eventos de seleccionar la Urna I, la Urna II y la Urna III.

Además, sea A el evento de que la bola extraída sea blanca.

Entonces, P(E 1 ) = 1/3

P(E 2 ) = 1/3

P(E3 ) = 1/3

Ahora,

P(A/E 1 ) = 2/5

P(A/E 2 ) = 3/5

P(A/E 3 ) = 4/5

Usando el teorema de Bayes, la probabilidad requerida es,

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) +P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{1}{3} \times \frac{2}{5}}{\frac{1}{3} \times \frac{2}{5} + \frac{1}{3} \times \frac{3}{5} + \frac{1}{3} \times \frac{4}{5}}

= \frac{2}{2 + 3 + 4}

= 2/9

Pregunta 4. El contenido de las tres urnas es el siguiente: 

Urna 1: 7 bolas blancas, 3 negras, Urna 2: 4 bolas blancas, 6 negras y Urna 3: 2 bolas blancas, 8 negras. Una de estas urnas se elige al azar con probabilidades de 0,20, 0,60 y 0,20 respectivamente. De la urna elegida se extraen dos bolas al azar sin reposición. Si estas dos bolas son blancas, ¿cuál es la probabilidad de que provengan de la urna 3?

Solución:

Supongamos que E 1 , E 2 y E 3 son los eventos de seleccionar Urna I, Urna II y Urna III. Además, sea A el evento de que las dos bolas extraídas sean blancas.

Entonces, P(E 1 ) = 20/100

P(E2 ) = 60/100

P( E3) = 20/100

Ahora,

P(A/E 1 ) =  \frac{{}^7 C_2}{{}^{10} C_2}  = 21/45

P(A/E 2 ) =  \frac{{}^4 C_2}{{}^{10} C_2}  = 6/45

P(A/E 3 ) =  \frac{{}^2 C_2}{{}^{10} C_2}  = 1/45

Usando el teorema de Bayes, la probabilidad requerida es,

P(E 3 /A) = \frac{P\left( E_3 \right)P\left( A/ E_3 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{20}{100} \times \frac{1}{45}}{\frac{20}{100} \times \frac{21}{45} + \frac{60}{100} \times \frac{6}{45} + \frac{20}{100} \times \frac{1}{45}}

= \frac{1}{21 + 18 + 1}

= 1/40

Pregunta 5. Supón que una niña lanza un dado. Si obtiene 1 o 2, lanza una moneda tres veces y anota el número de cruces. Si obtiene 3, 4, 5 o 6, lanza una moneda al aire una vez y anota si obtiene ‘cara’ o ‘cruz’. Si obtuvo exactamente una ‘cruz’, ¿cuál es la probabilidad de que haya sacado 3, 4, 5 o 6 con el dado?       

Solución:

Consideremos que E 1 es el evento de que el resultado del dado es 1 o 2 y E 2 es el evento de que el resultado del dado es 3, 4, 5 o 6. 

Ahora, P(E 1 ) = 2/6 = 1/3 y P(E 2 ) = 4/6 = 2/3

Además, supongamos que A es el evento de obtener exactamente una ‘cruz’.

Entonces, P(A/E 1 ) = 3/8

P(A/E 2 ) = 1/2

Ahora, P(E 2 /A) es la probabilidad de que la niña tire 3, 4, 5 o 6 con el dado, si saca exactamente una cruz

Entonces, usando el teorema de Bayes, la probabilidad requerida es,

P(E2 /A)  =\frac{P\left( E_2 \right) \times P\left( A/E_2 \right)}{P\left( E_1 \right) \times P\left( A/ E_1 \right) + P\left( E_2 \right) \times P\left( A/ E_2 \right)}

= \frac{\left( \frac{2}{3} \times \frac{1}{2} \right)}{\left( \frac{1}{3} \times \frac{3}{8} + \frac{2}{3} \times \frac{1}{2} \right)}

= \frac{ \frac{2}{6}}{ \frac{1}{8} + \frac{1}{3}}

= \frac{24 \times 2}{11 \times 6}

= 8/11

Pregunta 6. Dos grupos compiten por los cargos de la Junta Directiva de una Sociedad Anónima. Las probabilidades de que ganen el primer y el segundo grupo son 0,6 y 0,4 respectivamente. Además, si gana el primer grupo, la probabilidad de introducir un nuevo producto es 0,7 y la probabilidad correspondiente es 0,3 si gana el segundo grupo. Encuentre la probabilidad de que el nuevo producto introducido fuera del segundo grupo.

Solución:

Consideremos que E 1 y E 2 son los eventos en los que el primer grupo y el segundo grupo ganan la competencia. También, A ser el evento de introducir un nuevo producto.

Entonces, P(E 1 ) = 0.6

P(E2 ) = 0,4

P(A/E1 ) = 0,7

P(A/E2 ) = 0,3

Ahora, P(E 2 /A) es la probabilidad de que el nuevo producto sea introducido por el segundo grupo

Entonces, usando el teorema de Bayes, la probabilidad requerida es,

P(E2 /A)  =\frac{P\left( E_2 \right)P\left( A/ E_2 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{0 . 4 \times 0 . 3}{0 . 6 \times 0 . 7 + 0 . 4 \times 0 . 3}

= 0,12/0,54

= 2/9

Pregunta 7. Supongamos que 5 hombres de 100 y 25 mujeres de 1000 son buenos oradores. Se elige un orador al azar. Encuentre la probabilidad de que una persona masculina sea seleccionada. Suponga que hay igual número de hombres y mujeres.

Solución:

Supongamos que A, E 1 y E 2 son los eventos de que la persona es buena oradora, es hombre y es mujer.

Entonces, P(E 1 ) = 1/2

P(E 2 ) = 1/2

Ahora,

P(A/E 1 ) = 5/100

P(A/E 2 ) = 25/1000

Entonces, usando el teorema de Bayes, la probabilidad requerida es,

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{1}{2} \times \frac{5}{100}}{\frac{1}{2} \times \frac{5}{100} + \frac{1}{2} \times \frac{25}{1000}}

= \frac{1}{1 + \frac{1}{2}}

= 2/3

Pregunta 8. Se sabe que una carta vino de LONDRES o CLIFTON. En el sobre solo se ven dos letras ON consecutivas. ¿Cuál es la probabilidad de que la carta haya venido de

(i) LONDRES (ii) CLIFTON?

Solución:

Consideremos A, E 1 y E 2 como los eventos en que las dos letras consecutivas son visibles y la letra proviene de LONDON y CLIFTON.

Entonces, P(E 1 ) = 1/2

P(E 2 ) = 1/2

Ahora,

P(A/E 1 ) = 2/5

P(A/E 2 ) = 1/6

Entonces, usando el teorema de Bayes, la probabilidad requerida es,

(i) P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{1}{2} \times \frac{2}{5}}{\frac{1}{2} \times \frac{2}{5} + \frac{1}{2} \times \frac{1}{6}}

= \frac{\frac{2}{5}}{\frac{2}{5} + \frac{1}{6}}

= \frac{\frac{2}{5}}{\frac{17}{30}}

= 12/17

(ii) P(E 2 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{1}{2} \times \frac{1}{6}}{\frac{1}{2} \times \frac{2}{5} + \frac{1}{2} \times \frac{1}{6}}

= \frac{\frac{1}{6}}{\frac{2}{5} + \frac{1}{6}}

= \frac{\frac{1}{6}}{\frac{17}{30}}

= 5/17

Pregunta 9. En una clase, el 5% de los niños y el 10% de las niñas tienen un coeficiente intelectual de más de 150. En esta clase, el 60% de los estudiantes son niños. Si se selecciona un estudiante al azar y se encuentra que tiene un coeficiente intelectual de más de 150, encuentre la probabilidad de que el estudiante sea un niño.

Solución:

Consideremos A, E 1 y E 2 como los eventos en los que el coeficiente intelectual es superior a 150, el estudiante seleccionado es un niño y la estudiante seleccionada es una niña.

Entonces, P(E 1 ) = 60/100

P(E2 ) = 40/100

Ahora,

P(A/E 1 ) = 5/100

P(A/E 2 ) = 10/100

Entonces, usando el teorema de Bayes, la probabilidad requerida es,

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{60}{100} \times \frac{5}{100}}{\frac{60}{100} \times \frac{5}{100} + \frac{40}{100} \times \frac{10}{100}}

= \frac{300}{300 + 400}

= 300/700

= 3/7

Pregunta 10. Una fábrica tiene tres máquinas, X, Y y Z que producen 1000, 2000 y 3000 pernos por día, respectivamente. La máquina X produce 1% de pernos defectuosos, Y produce 1,5% y Z produce 2% de pernos defectuosos. Al final del día, se extrae un perno al azar y se encuentra defectuoso. ¿Cuál es la probabilidad de que este perno defectuoso haya sido producido por la máquina X?

Solución:

Supongamos que E 1 , E 2 y E 3 son los eventos de que la máquina X produce pernos, la máquina Y produce pernos y la máquina Z produce pernos. Además, A será el evento de que el perno esté defectuoso.

Entonces, el número total de pernos = 1000 + 2000 + 3000 = 6000

P(E1 ) = 1000/6000 = 1/6

P(E 2 ) = 2000/6000 = 1/3

P(E 3 ) = 3000/6000 = 1/2

Ahora, P(E 1 /A) es la probabilidad de que el perno defectuoso sea producido por la máquina X

Asi que, 

P(A/E 1 ) = 1% = 1/100

P(A/E 2 ) = 1,5% = 15/1000

P(A/E 3 ) = 2% = 2/100

Entonces, usando el teorema de Bayes, la probabilidad requerida es,

P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}

= \frac{\frac{1}{6} \times \frac{1}{100}}{\frac{1}{6} \times \frac{1}{100} + \frac{1}{3} \times \frac{15}{1000} + \frac{1}{2} \times \frac{2}{100}}

= \frac{\frac{1}{6}}{\frac{1}{6} + \frac{1}{2} + 1}

= \frac{\frac{1}{6}}{\frac{1 + 3 + 6}{6}}

= 1/10

Pregunta 11. Una compañía de seguros aseguró 3000 scooters, 4000 automóviles y 5000 camiones. Las probabilidades de que ocurra un accidente con un scooter, un automóvil y un camión son 0,02, 0,03 y 0,04, respectivamente. Uno de los vehículos asegurados sufre un accidente. Encuentre la probabilidad de que sea un (i) scooter (ii) automóvil (iii) camión. 

Solución:

Supongamos que E 1 , E 2 y E 3 son los eventos de que el vehículo es un scooter, un automóvil y un camión. Asimismo, será A el evento de que el vehículo sufra un accidente.

Según la pregunta, la compañía de seguros aseguró 3000 scooters, 4000 automóviles y 5000 camiones.

Entonces, el número total de vehículos = 3000 + 4000 + 5000 = 12000

P(E1 ) = 3000/12000 = 1/4

P(E2 ) = 4000/12000 = 1/3

P(E 3 ) = 5000/12000 = 5/12

Ahora bien, P(E 1 /A) es la probabilidad de que el vehículo que sufre el accidente sea una scooter 

Ahora,

P(A/E 1 ) = 0.02 = 2/100

P(A/E 2 ) = 0,03 = 3/100

P(A/E 3 ) = 0.04 = 4/100

Entonces, usando el teorema de Bayes, la probabilidad requerida es,

(i) P(E 1 /A) = \frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{1}{4} \times \frac{2}{100}}{\frac{1}{4} \times \frac{2}{100} + \frac{1}{3} \times \frac{3}{100} + \frac{5}{12} \times \frac{4}{100}}

= \frac{\frac{1}{2}}{\frac{1}{2} + 1 + \frac{5}{3}}

= \frac{\frac{1}{2}}{\frac{3 + 6 + 10}{6}}

= 3/19

(ii) P(E 2 /A) = \frac{P\left( E_2 \right)P\left( A/ E_2 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{1}{3} \times \frac{3}{100}}{\frac{1}{4} \times \frac{2}{100} + \frac{1}{3} \times \frac{3}{100} + \frac{5}{12} \times \frac{4}{100}}

= \frac{1}{\frac{1}{2} + 1 + \frac{5}{3}}

= \frac{1}{\frac{3 + 6 + 10}{6}}

= 6/19

(iii) P(E 3 /A) = \frac{P\left( E_3 \right)P\left( A/ E_3 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}

= \frac{\frac{5}{12} \times \frac{4}{100}}{\frac{1}{4} \times \frac{2}{100} + \frac{1}{3} \times \frac{3}{100} + \frac{5}{12} \times \frac{4}{100}}

= \frac{\frac{5}{3}}{\frac{1}{2} + 1 + \frac{5}{3}}

= \frac{\frac{5}{3}}{\frac{3 + 6 + 10}{6}}

= 10/19

Pregunta 12. Supongamos que tenemos cuatro cajas A, B, C, D que contienen canicas de colores como se indica a continuación:

Caja

        Color

 

Rojo

Blanco

Negro

A

1

6

3

B

6

2

2

C

8

1

1

D

0

6

4

Una de las cajas ha sido seleccionada al azar y de ella se extrae una sola canica. Si la canica es roja, ¿cuál es la probabilidad de que haya sido extraída de la caja A, la caja B y la caja C?

Solución:

Supongamos que R es el evento de sacar la canica roja y E A , E B y E C son los eventos de seleccionar la casilla A, la casilla B y la casilla C.

Según la pregunta, el número total de canicas es 40 y el número de canicas rojas es 15.

Entonces, P(R) = 15/40 = 3/8

P(E A /R) = La probabilidad de sacar una canica roja de la caja A.

P(E A /R) = \frac{P\left( E_A \cap R \right)}{P\left( R \right)}

= \frac{\frac{1}{40}}{\frac{3}{8}}

= 1/15

P(E B /R) = La probabilidad de sacar una canica roja de la caja B.

P(E B /R \right) = \frac{P\left( E_B \cap R \right)}{P\left( R \right)}

= \frac{\frac{6}{40}}{\frac{3}{8}}

= 2/5

P(E C /R) = La probabilidad de sacar una canica roja de la caja C.

P(E C /R) = \frac{P\left( E_C \cap R \right)}{P\left( R \right)}

= \frac{\frac{8}{40}}{\frac{3}{8}}

= 8/15

Pregunta 13. Un fabricante tiene tres operadores de máquinas, A, B y C. El primer operador, A, produce el 1 % de artículos defectuosos, mientras que los otros dos operadores, B y C, producen el 5 % y el 7 % de artículos defectuosos, respectivamente. A está en el trabajo el 50% del tiempo, B en el trabajo el 30% del tiempo y C en el trabajo el 20% del tiempo. Se produce un artículo defectuoso. ¿Cuál es la probabilidad de que haya sido producido por A?

Solución:

Consideremos que E 1 , E 2 y E 3 son el tiempo que tardan los operadores de máquinas A, B y C. Además, X es el evento de producir artículos defectuosos.

P(E 1 ) = 50 % = 1/2

P(E 2 ) = 30 % = 3/10

P(E 3 ) = 20 % = 1/5

Ahora,

P(X/E 1 ) = 1 % = 1/100

P(X/E 2 ) = 5 % = 5/100

P(X/E 3 ) = 7 % = 7/100

Entonces, usando el teorema de Bayes, la probabilidad requerida es,

P(E 1 /X) = \frac{P\left( E_1 \right)P\left( X/ E_1 \right)}{P\left( E_1 \right)P\left( X/ E_1 \right) + P\left( E_2 \right)P\left( X/ E_2 \right) + P\left( E_3 \right)P\left( X/ E_3 \right)}

= \frac{\frac{1}{2} \times \frac{1}{100}}{\frac{1}{2} \times \frac{1}{100} + \frac{3}{10} \times \frac{5}{100} + \frac{1}{5} \times \frac{7}{100}}

= 5/34

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *