Clase 12 RD Sharma Solutions – Capítulo 33 Distribución binomial – Ejercicio 33.1 | conjunto 2

Posted on by Rudeus Greyrat

Pregunta 19. Una bolsa contiene 7 bolas verdes, 4 blancas y 5 rojas. Si se extraen cuatro bolas una por una con reposición, ¿cuál es la probabilidad de que una sea roja?

Solución:

el número de bolas rojas extraídas de 16 bolas con reemplazo.

= 4.

Aquí, p = 5/16 y q = 1 – p = 11/16

P(X = r) = ^{4}{}{C}_r \left( \frac{5}{16} \right)^r \left( \frac{11}{16} \right)^{4 - r}

P(Una bola es roja) = P(X = 1)

= ^{4}{}{C}_1 \left( \frac{5}{16} \right)^1 \left( \frac{11}{16} \right)^{4 - 1}

= 4 (5/16) (11/16) 3

= (5/4) (11/16) 3

Pregunta 20. Una bolsa contiene 2 bolas blancas, 3 rojas y 4 azules. Se extraen dos bolas al azar de la bolsa. Si X denota el número de bolas blancas entre las dos bolas extraídas, describa la distribución de probabilidad de X.

Solución:

Sea X el número de bolas blancas cuando se extraen 2 bolas de la bolsa.

X sigue una distribución con valores 0, 1 o 2.

P(X = 0) = P(Todas las bolas no son blancas) 

= \frac{^{7}{}{C}_2}{^{9}{}{C}_2}

= 42/72

= 21/36

P(X = 1) = P (I primera bola blanca y II segunda bola no blanca)

= \frac{^{7}{}{C}_1 ^{2}{}{C}_1}{^{9}{}{C}_2}

= 14/36

Entonces, P(X = 2) = P(Ambas bolas blancas) 

= \frac{^{2}{}{C}_2}{^{9}{}{C}_2}

= 1/36

Entonces, la forma tabular es:

X

0

1

2

P(X)

21/36

14/36

1/36

Pregunta 21. Una urna contiene cuatro bolas blancas y tres rojas. Encuentre la distribución de probabilidad del número de bolas rojas en tres sorteos con reemplazo de la urna.

Solución:

Dado que se extraen tres bolas con un reemplazo, el número de bolas blancas.

= 3.

Aquí p = 3/7 y q = 4/7

P(X = r) =  ^{3}{}{C}_r \left( \frac{3}{7} \right)^r \left( \frac{4}{7} \right)^{3 - r}  , r = 0, 1, 2, 3

P(X = 0) = ^{3}{}{C}_0 \left( \frac{3}{7} \right)^0 \left( \frac{4}{7} \right)^{3 - 0}

= 64/343

P(X = 1) = ^{3}{}{C}_1 \left( \frac{3}{7} \right)^1 \left( \frac{4}{7} \right)^{3 - 1}

= 144/343

P(X = 2) = ^{3}{}{C}_2 \left( \frac{3}{7} \right)^2 \left( \frac{4}{7} \right)^{3 - 2}

= 108/343

P(X = 3) = ^{3}{}{C}_3 \left( \frac{3}{7} \right)^3 \left( \frac{4}{7} \right)^{3 - 3}

= 27/343

Entonces, la forma tabular es:

X

0

1

2

3

P(X)

64/343

144/343

108/343

27/343

Pregunta 22. Encuentra la distribución de probabilidad del número de dobletes en 4 lanzamientos de un par de dados.

Solución:

Consideremos que X denota el número de dobletes en 4 lanzamientos de un par de dados.

= 4.

Aquí p = No de obtener (1, 1)(2, 2) . . . (6, 6) 

= 6/36

= 1/6

Y q = 1 – p = 5/6

P(X = r) =  ^{4}{}{C}_r \left( \frac{1}{6} \right)^r \left( \frac{5}{6} \right)^{4 - r} , r = 0, 1, 2, 3, 4

P(X = 0) = ^{4}{}{C}_0 \left( \frac{1}{6} \right)^0 \left( \frac{5}{6} \right)^{4 - 0}

= 625/1296

P(X = 1) = ^{4}{}{C}_1 \left( \frac{1}{6} \right)^1 \left( \frac{5}{6} \right)^{4 - 1}

= 500/1296

P(X = 2) = ^{4}{}{C}_2 \left( \frac{1}{6} \right)^2 \left( \frac{5}{6} \right)^{4 - 2}

= 150/1296

P(X = 3) = ^{4}{}{C}_3 \left( \frac{1}{6} \right)^3 \left( \frac{5}{6} \right)^{4 - 3}

= 20/1296

P(X = 4) = ^{4}{}{C}_4 \left( \frac{1}{6} \right)^4 \left( \frac{5}{6} \right)^{4 - 4}

= 1/1296

Entonces, la distribución es:

X

0

1

2

3

4

P(X)

625/1296

500/1296

150/1296

20/1296

1/1296

Pregunta 23. Encuentra la distribución de probabilidad del número de seises en tres lanzamientos de un dado.

Solución:

Consideremos que X denota el número de 6 en 3 lanzamientos de un dado.

= 3.

Aquí p = 1/6, q = 1 – p = 5/6

P(X = r) =  ^{3}{}{C}_r \left( \frac{1}{6} \right)^r \left( \frac{5}{6} \right)^{3 - r} , r = 0, 1, 2, 3

Entonces, P(X = 0) = ^{3}{}{C}_0 \left( \frac{1}{6} \right)^0 \left( \frac{5}{6} \right)^{3 - 0}

= 125/216

P(X = 1) = ^{3}{}{C}_1 \left( \frac{1}{6} \right)^1 \left( \frac{5}{6} \right)^{3 - 1}

= 75/216

P(X = 2) = ^{3}{}{C}_2 \left( \frac{1}{6} \right)^2 \left( \frac{5}{6} \right)^{3 - 2}

= 15/216

P(X = 3) = ^{3}{}{C}_3 \left( \frac{1}{6} \right)^3 \left( \frac{5}{6} \right)^{3 - 3}

= 1/216

Entonces, la distribución es:

X

0

1

2

3

P(X)

125/216

75/216

15/216

1/216

Pregunta 24. Se lanza una moneda 5 veces. Si X es el número de caras observadas, encuentre la distribución de probabilidad de X.

Solución:

Consideremos que X denota el número de caras en 5 lanzamientos. 

= 5.

Aquí p = 1/2 y q = 1/2

P(X = r) =  ^{5}{}{C}_r \left( \frac{1}{2} \right)^r \left( \frac{1}{2} \right)^{5 - r} , r = 0, 1, 2, 3, 4, 5

= 5 C r (2) 5

P(X = 0) = 5 C 0 (2) 5

= 1/32

P(X = 1) = 5 C 1 (2) 5

= 5/32

P(X = 2) = 5 C 2 (2) 5

= 10/32

P(X = 3) = 5 C 3 (2) 5

= 10/32

P(X = 4) = 5 C 4 (2) 5

= 5/32

P(X = 5) = 5C 5 (2) 5

= 1/32

Entonces, la distribución es:

X

0

1

2

3

4

5

P(X)

1/32

5/32

32/10

32/10

5/32

1/32

Pregunta 25. Se lanza un dado sin sesgo dos veces. Un éxito es obtener un número mayor que 4. Encuentra la distribución de probabilidad del número de éxitos.

Solución:

Consideremos X ser la obtención de un número mayor que 4 .

= 2

Aquí p = P(X > 4) = P(X = 5 o 6)

= 1/6 + 1/6

= 1/3

Y q = 1 – p = 2/3

PAG(X = r) =  ^{2}{}{C}_r \left( \frac{1}{3} \right)^r \left( \frac{2}{3} \right)^{2 - r} , r = 0, 1, 2

Entonces, la distribución es:

X

0

1

2

P(X)

4/9

4/9

1/9

Pregunta 26. Un hombre gana una rupia por cara y pierde una rupia por cruz cuando se lanza una moneda. Supongamos que lanza una vez y abandona si gana, pero intenta una vez más si pierde en el primer lanzamiento. Encuentre la distribución de probabilidad del número de rupias que gana el hombre.

Solución:

Consideremos X el número de rupias que gana el hombre.

Entonces, primero asumimos que obtiene cara en el primer lanzamiento.

Entonces, la probabilidad sería 1/2. Además, gana Rs.1 rupia.

Ahora, la segunda posibilidad es que obtenga cruz en el primer lanzamiento.

Luego vuelve a lanzar. Supongamos que obtiene adelante en el segundo lanzamiento.

Luego, gana Rs 1 rupia en el segundo lanzamiento, pero pierde Rs 1 rupia en el primer lanzamiento.

Entonces, el dinero que ganó = Rs 0

Entonces, la probabilidad de ganar Rs.0 es 

= (1/2) (1/2)

= 1/4

Ahora, la tercera posibilidad es obtener cruz en el primer lanzamiento y también cruz en el segundo lanzamiento.

Entonces, el dinero que ganaría = -2 (Ya que pierde Rs 2)

Entonces, la probabilidad de la tercera posibilidad = (1/2) (1/2)

= 1/4

Entonces, la distribución es:

X

0

1

2

P(X)

1/2

1/4

1/4

Pregunta 27. Se lanzan cinco dados simultáneamente. Si la ocurrencia de 3, 4 o 5 en un solo dado se considera un éxito, encuentre la probabilidad de al menos 3 éxitos.

Solución:

Consideremos X la ocurrencia de 3, 4 o 5 en un solo dado. 

= 5.

Supongamos que la probabilidad de obtener 3, 4 o 5 en un solo dado es p

Aquí p = 3/6 = 1/2

Y q = 1 – 1/2 = 1/2

P(X = r) = ^{5}{}{C}_r \left( \frac{1}{2} \right)^r \left( \frac{1}{2} \right)^{5 - r}

P(al menos 3 éxitos) = P(X > 3)

= P(X = 3) + P(X = 4) + P(X = 5)

= ^{5}{}{C}_3 \left( \frac{1}{2} \right)^3 \left( \frac{1}{2} \right)^{5 - 3} + ^{5}{}{C}_4 \left( \frac{1}{2} \right)^4 \left( \frac{1}{2} \right)^{5 - 4} +^{5}{}{C}_5 \left( \frac{1}{2} \right)^5 \left( \frac{1}{2} \right)^{5 - 5}

= \frac{^{5}{}{C}_3 + ^{5}{}{C}_4 + ^{5}{}{C}_5}{2^5}

= 16/32

= 1/2

Pregunta 28. Los artículos producidos por una empresa contienen un 10% de artículos defectuosos. Muestre que la probabilidad de obtener 2 artículos defectuosos en una muestra de 8 artículos es 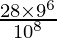 \frac{28 \times 9^6}{{10}^8} .

Solución:

Consideremos que X es el número de artículos defectuosos en los artículos producidos por la empresa.

= 8.

Aquí, p = 10 % = 10/100 = 1/10

Y q = 1 – p = 9/10

Por lo tanto, la distribución está dada por,

P(X = r) = ^{8}{}{C}_r \left( \frac{1}{10} \right)^r \left( \frac{9}{10} \right)^{8 - r}

Entonces, la probabilidad de obtener 2 artículos defectuosos es

P(X = 2) = ^{8}{}{C}_2 \left( \frac{1}{10} \right)^2 \left( \frac{9}{10} \right)^{8 - 2}

= \frac{28 \times 9^6}{{10}^8}

Por lo tanto probado.

Pregunta 29. Se extrae una carta y se reemplaza en un paquete ordinario de 52 cartas. ¿Cuántas veces se debe sacar una carta para que 

(i) hay al menos una probabilidad pareja de sacar un corazón 

Solución:

Consideremos X como la probabilidad de sacar un corazón de una baraja de 52 cartas. 

Entonces, obtenemos

Aquí, p = 13/52 = 1/4

Y q = 1 – p = 1 – 1/4 = 3/4

Supongamos que la carta se saca n veces. 

Asi que, 

P(X = r) = ^{n}{}{C}_r p^r q^{n - r}

Consideremos X el número de corazones extraídos de un paquete de 52 cartas.

Entonces, el valor más pequeño de n para el cual P(X=0) es menor que 1/4

es decir, P(X = 0) < 1/4

^{n}{}{C}_0 \left( \frac{1}{4} \right)^0 \left( \frac{3}{4} \right)^{n - 0} < \frac{1}{4}

=> \left( \frac{3}{4} \right)^n < \frac{1}{4}

Ahora, ponga n = 1, (3/4) 1 no menos de 1/4

n = 2, (3/4) 2 no menos de 1/4

n = 3, (3/4) 3 no menos de 1/4

Entonces, el valor más pequeño de n = 3.

(ii) la probabilidad de sacar un corazón es mayor que 3/4

Solución:

Dado que la probabilidad de sacar un corazón > 3/4.

entonces, 1 – P(X = 0) > 3/4

1 -^{n}{}{C}_0 \left( \frac{1}{4} \right)^0 \left( \frac{3}{4} \right)^{n - 0} > \frac{3}{4}

1 - \left( \frac{3}{4} \right)^n > \frac{3}{4}

1 - \frac{3}{4} > \left( \frac{3}{4} \right)^n

\frac{1}{4} > \left( \frac{3}{4} \right)^n

Para n = 1, (3/4) 1 no menos de 1/4.

n = 2, (3/4) 2 no menos de 1/4

n = 3, (3/4) 3 no menos de 1/4

n = 4, (3/4) 4 no menos de 1/4

n = 5, (3/4) 5 no menos de 1/4

Por lo tanto, la carta debe ser extraída 5 veces.

Pregunta 30. El departamento de matemáticas tiene 8 asistentes graduados que están asignados a la misma oficina. Es tan probable que cada asistente estudie en casa como en la oficina. ¿Cuántos escritorios debe haber en la oficina para que cada asistente tenga un escritorio al menos el 90% del tiempo?

Solución:

Consideremos que k denota el número de escritorios y X denota el número de asistentes graduados en la oficina.

= 8.

Aquí p = 1/2 y q = 1/2.

Asi que, 

=> P(X < k) > 90%  

=> P\izquierda( X < k \derecha) > 0.90

=> P\izquierda( X > k \derecha) < 0.10

=> PAG(X = k + 1, k + 2, . . . . 8) < 0 . 10

Por lo tanto, P(X > 6) = P(X = 7 o X = 8)

^{8}{}{C}_7 \left( \frac{1}{2} \right)^8 + ^{8}{}{C}_8 \left( \frac{1}{2} \right)^8 = 0.04

Ahora, P(X > 5) = P(X = 6, X = 7 o X = 8) = 0.15

P(X > 6) < 0,10

Por lo tanto, si hay 6 escritorios, hay al menos un 90% de posibilidades de que cada graduado obtenga un escritorio.

Pregunta 31. Se lanza 8 veces una moneda imparcial. Encuentre, utilizando una distribución binomial, la probabilidad de obtener al menos 6 caras.

Solución:

Consideremos X el número de caras al lanzar la moneda 8 veces.

= 8.

Aquí p = 1/2 y q = 1/2

Por eso, 

P(X = r) =  ^{8}{}{C}_r \left( \frac{1}{2} \right)^r \left( \frac{1}{2} \right)^{8 - r} , r = 0, 1, 2, 3, 4, 5, 6, 7, 8

Entonces, la probabilidad requerida es 

P(X > 6) = P(X = 6) + P(X = 7) + P(X = 8)

= \frac{^{8}{}{C}_6 + ^{8}{}{C}_7 + ^{8}{}{C}_8}{2^8}

= \frac{28 + 8 + 1}{256}

= 37/256

Pregunta 32. Se lanzan seis monedas simultáneamente. Encuentre la probabilidad de obtener:

(yo) 3 cabezas

Solución:

Consideremos X el número de caras obtenidas al lanzar 6 monedas.

= 6.

Aquí p = 1/2 y q = 1/2

Por eso, 

P(X = r) =  ^{6}{}{C}_r \left( \frac{1}{2} \right)^r \left( \frac{1}{2} \right)^{6 - r} , r = 0, 1, 2, 3, 4, 5, 6

= \frac{^{6}{}{C}_r}{2^6}

P(obtener 3 caras) = ​​P(X = 3)

= \frac{^{6}{}{C}_3}{2^6}

= 20/64

= 5/16

(ii) sin cabezas

Solución:

P(no obtener cabeza) = P(X = 0)

= \frac{^{6}{}{C}_0}{2^6}

= (1/2) 6

= 1/64

(iii) al menos una cabeza

Solución:

P(obtener al menos 1 cara) = P(X > 1)

= 1 – P(X = 0)

= 1 – 1/64

= 63/64

Pregunta 33. Suponga que un tubo de radio insertado en cierto tipo de aparato tiene una probabilidad de 0.2 de funcionar más de 500 horas. Si probamos 4 tubos al azar, ¿cuál es la probabilidad de que exactamente tres de estos tubos funcionen durante más de 500 horas?

Solución:

Consideremos X el número de tubos que funcionan más de 500 horas.  

= 4.

Consideremos p la probabilidad de que los tubos funcionen más de 500 horas.

Aquí, p = 0,2, q = 0,8

Por eso, 

P(X = r) = 4 C r (0.2) r (0.8) 4-r , r = 0, 1, 2, 3, 4

Entonces, la probabilidad requerida es 

P(X = 3) = 4 (0,2) 3 (0,8)

= 0.0256

Pregunta 34. La probabilidad de que cierto tipo de componente sobreviva a una prueba de choque determinada es 3/4. 

(i) Encuentre la probabilidad de que entre 5 componentes probados exactamente 2 sobrevivan.

Solución:

Consideremos X el número de componentes que sobreviven al choque.

= 5.

Consideremos p como la probabilidad de que cierto tipo de 

componente sobrevivirá a una prueba de choque determinada.  

Entonces, p = 3/4 y q = 1/4

Por eso, 

P(X = r) =  ^{5}{}{C}_r \left( \frac{3}{4} \right)^r \left( \frac{1}{4} \right)^{5 - r}  , r = 0, 1, 2, 3, 4, 5

P(sobrevivirán exactamente 2} ) = P(X = 2) 

= ^{5}{}{C}_2 \left( \frac{3}{4} \right)^2 \left( \frac{1}{4} \right)^{5 - 2}

= \frac{10 \times 9}{1024}

= 0.0879

(ii) Encuentre la probabilidad de que entre 5 componentes probados como máximo 3 sobrevivan.

Solución:

Consideremos X el número de componentes que sobreviven al choque.

= 5.

Consideremos p como la probabilidad de que cierto tipo de 

componente sobrevivirá a una prueba de choque determinada.

Entonces, p = 3/4 y q = 1/4

Por eso, 

P(X = r) =  ^{5}{}{C}_r \left( \frac{3}{4} \right)^r \left( \frac{1}{4} \right)^{5 - r} , r = 0, 1, 2, 3, 4, 5

P(a lo sumo 3 sobrevivirán) = P(X < 3)

= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)

= ^{5}{}{C}_{0} \left( \frac{3}{4} \right)^0 \left( \frac{1}{4} \right)^{5 - 0} + ^{5}{}{C}_1 \left( \frac{3}{4} \right)^1 \left( \frac{1}{4} \right)^{5 - 1} + ^{5}{}{C}_2 \left( \frac{3}{4} \right)^2 \left( \frac{1}{4} \right)^{5 - 2} + ^{5}{}{C}_3 \left( \frac{3}{4} \right)^3 \left( \frac{1}{4} \right)^{5 - 3}

= \left( \frac{1}{4} \right)^5 + 5\left( \frac{3}{4} \right) \left( \frac{1}{4} \right)^4 + 10 \left( \frac{3}{4} \right)^2 \left( \frac{1}{4} \right)^3 + 10 \left( \frac{3}{4} \right)^3 \left( \frac{1}{4} \right)^2

= \frac{1 + 15 + 90 + 270}{1024}

= 376/1024

= 0.3672

Pregunta 35. Suponga que la probabilidad de que una bomba lanzada desde un avión golpee cierto objetivo es 0.2. Si se lanzan 6 bombas, encuentre la probabilidad:

(i) que exactamente 2 darán en el blanco.

Solución:

Consideremos X el número de bombas que impactan en el blanco y 

Sea p la probabilidad de que una bomba lanzada desde un avión dé en el blanco.

 = 6

p = 0,2 y q = 0,8

Por eso, 

P(X = r) = ^{6}{}{C}_r \left( 0 . 2 \right)^r \left( 0 . 8 \right)^{6 - r}

P(exactamente 2 darán en el blanco) = P(X = 2)

= ^{6}{}{C}_2 (0 . 2 )^2 (0 . 8 )^4

= 0.2458

(ii) que al menos 2 darán en el blanco

Solución:

Consideremos X el número de bombas que impactan en el blanco y

Sea p la probabilidad de que una bomba lanzada desde un avión dé en el blanco.

= 6.

p = 0,2 y q = 0,8

Por eso, 

P(X = r) = ^{6}{}{C}_r \left( 0 . 2 \right)^r \left( 0 . 8 \right)^{6 - r}

P(al menos 2 darán en el blanco) = P(X > 2)

= 1 – [P(X = 0) + P(X = 1)]

= 1 – (0,8) 6 – 6 (0,2) (0,8) 5

= 1 – 0,2621 – 0,3932

= 0 . 3447

Pregunta 36. Se sabe que el 60% de los ratones inoculados con suero están protegidos contra una determinada enfermedad. Si se inoculan 5 ratones, encuentre la probabilidad de que: 

(i) ninguno contrae la enfermedad.

Solución:

Consideremos X el número de ratones que contraen la enfermedad y

sea ​​p la probabilidad de que los ratones contraigan la enfermedad.

 = 5.

 p = 0,4 y q = 0,6

Por eso, 

P(X = r) =  ^{5}{}{C}_r \left( 0 . 4 \right)^r \left( 0 . 6 \right)^{5 - r} , r = 0, 1, 2, 3, 4, 5

P(X = 0) = ^{5}{}{C}_0 \left( 0 . 4 \right)^0 \left( 0 . 6 \right)^{5 - 0}

= (0.6) 5

= 0.0778

(ii) más de 3 contraen la enfermedad.

Solución:

Consideremos X el número de ratones que contraen la enfermedad y

 sea ​​p la probabilidad de que los ratones contraigan la enfermedad.

 = 5.

 p = 0,4 y q = 0,6

Por eso, 

P(X = r) =  ^{5}{}{C}_r \left( 0 . 4 \right)^r \left( 0 . 6 \right)^{5 - r} , r = 0, 1, 2, 3, 4, 5

P(X > 3) = P(X = 4) + P(X = 5)

= ^{5}{}{C}_4 \left( 0 . 4 \right)^4 \left( 0 . 6 \right)^{5 - 4} +^{5}{}{C}_5 \left( 0 . 4 \right)^5 \left( 0 . 6 \right)^{5 - 5}

= 0,0768 + 0,01024

= 0.08704

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *