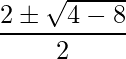Clase 12 RD Sharma Solutions- Capítulo 5 Álgebra de Arrays – Ejercicio 5.1

Pregunta 11: Encuentra x, y y z para que A = B, donde A= $\begin{bmatrix} x-2 & 3 & 2z\\ 18z & y+2 & 6z \end{bmatrix} = \begin{bmatrix} y & z & 6\\ 6y & x & 2y \end{bmatrix}$ .

Solución:

Como se da que las arrays son iguales, cada elemento en un índice dado en el lado izquierdo (LHS) debe ser igual al elemento en el mismo índice en el lado derecho (RHS).

De este modo,

a ₁₁ : x-2 = y ………….(ecuación 1)

a ₁₂ : z = 3 ………….(ecuación 2)

a ₁₃ : 2z = 6 ………….(ecuación 3)

a ₂₁ : 18z = 6y ……….(ecuación 4)

a ₂₂ : y+2 = x ………..(ecuación 5)

a ₂₃ : 6z = 2y …………(ecuación 6)

De (eq.2) y (eq.3),

=> z = 3

De (eq.4) y (eq.6),

=> y = 3z

=> y = 3(3)

=> y = 9

Sustituir ( y=9 ) en (eq.1),

=> x-2 = 9

=> x = 11

Así x=11, y=9 yz=3.

Pregunta 12: Si 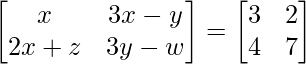$\begin{bmatrix} x & 3x-y\\ 2x+z & 3y-w \end{bmatrix} = \begin{bmatrix} 3 & 2\\ 4 & 7 \end{bmatrix}$ , encuentra x, y, z y w.

Solución:

Como se da que las arrays son iguales, cada elemento en un índice dado en el lado izquierdo (LHS) debe ser igual al elemento en el mismo índice en el lado derecho (RHS).

De este modo,

a ₁₁ : x = 3 ………….(ecuación 1)

a ₁₂ : 3x-y = 2 ………….(ecuación 2)

a ₂₁ : 2x+z = 4 ………..(ecuación 3)

a ₂₂ : 3y-w = 7 ……….(ecuación 4)

De (ec.1) ,

=> x = 3

Sustituye (x=3) en (eq.2),

=> 3(3)-y = 2

=> y = 3(3) – 2

=> y = 7

Sustituir ( x=3 ) en (eq.3),

=> 2(3)+z = 4

=>z = 4-6

=> z = -2

Sustituir (y=7) en (eq.4),

=>3(7) – w = 7

=>w = 21 – 7

=> w = 14

Así x=3, y=7, z=-2 y w=14.

Pregunta 13: Si 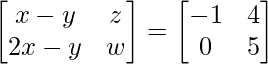$\begin{bmatrix} x-y & z \\ 2x-y & w \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ 0 & 5 \end{bmatrix}$ , encuentra x, y, z y w.

Como se da que las arrays son iguales, cada elemento en un índice dado en el lado izquierdo (LHS) debe ser igual al elemento en el mismo índice en el lado derecho (RHS).

De este modo,

a ₁₁ : xy = -1 ………….(ecuación 1)

a ₁₂ : z = 4 ………….(ecuación 2)

a ₂₁ : 2x-y = 0 ………..(ecuación 3)

a ₂₂ : w = 5 …………….(ecuación 4)

De (ecuación 2),

=> z = 4

Y de (ec.4),

=> w = 5

Ahora, (eq.1) y (eq.3) forman un sistema de ecuaciones que comprende las variables x e y.

Así, (ecuación 1) – (ecuación 2),

=> (x-2x) +(-y+y) = -1 – 0

=> -x = -1

=> x = 1

Sustituir (x=1) en (eq.1),

=> 1-y = -1

=> y = 2

Así, x=1, y=2, z=4 y w=5.

Pregunta 14: Si 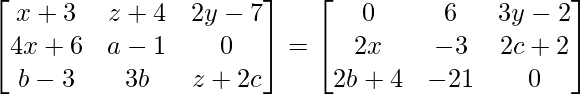$\begin{bmatrix} x+3 & z+4 & 2y-7\\ 4x+6 & a-1 & 0\\ b-3 & 3b & z+2c \end{bmatrix} = \begin{bmatrix} 0 & 6 & 3y-2\\ 2x & -3 & 2c+2\\ 2b+4 & -21 & 0 \end{bmatrix}$ . Obtenga los valores de a, b, c, x, y y z.

Solución:

Como se da que las arrays son iguales, cada elemento en un índice dado en el lado izquierdo (LHS) debe ser igual al elemento en el mismo índice en el lado derecho (RHS).

De este modo,

a ₁₁ : x+3 = 0 ……………..(ecuación 1)

a ₁₂ : z+4 = 6 ………….(ecuación 2)

a ₁₃ : 2y-7 = 3y-2 ……..(ec.3)

a ₂₁ : 4x+6 = 2x ………….(ecuación 4)

a ₂₂ : a-1 = -3 ……………..(ecuación 5)

a ₂₃ : 0 = 2c+2 …………….(ecuación 6)

a ₃₁ : b-3 = 2b+4…………(ecuación 7)

a ₃₂ : 3b = -21………………(ecuación 8)

a ₃₃ : z+2c = 0………………(ecuación 9)

De (eq.1) y (eq.4),

=> x = -3

De (ecuación 2),

=> z+4 = 6

=> z = 2

De (ecuación 3),

=> 2y-7 = 3y-2

=> 3y-2y = -7+2

=> y = -5

De (ecuación 5),

=> un = -3+1

=> un = -2

De (ecuación 8),

=> 3b = -21

=> segundo = -7

Sustituir (z=2) en (eq.9),

=> 2+ 2c = 0

=> c = -1

Así, x=-3, y=-5, z=2, a=-2, b=-7 y c=-1.

Pregunta 15: Si 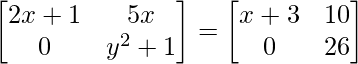$\begin{bmatrix} 2x+1 & 5x \\ 0 & y^2+1 \end{bmatrix} = \begin{bmatrix} x+3 & 10 \\ 0 & 26 \end{bmatrix}$ , encuentra el valor de (x+y).

Solución:

Como se da que las arrays son iguales, cada elemento en un índice dado en el lado izquierdo (LHS) debe ser igual al elemento en el mismo índice en el lado derecho (RHS).

De este modo,

a ₁₁ : 2x+1 = x+3………..(ecuación 1)

a ₁₂ : 5x = 10 ………………(ecuación 2)

a ₂₁ : 0 = 0 …………………(ecuación 3)

a ₂₂ : y ² +1 = 26 …………(ecuación 4)

De (eq.1) y (eq.2),

=> 2x+1 = x+3

=> x=2

De (ecuación 4),

=> y ² +1 = 26

=> y ² = 25

=> y = ± 5

Así si y = +5,

=> x+y = 7

Y si y = -5,

=> x+y = -3

Pregunta 16: Si $\begin{bmatrix} xy & 4 \\ z+6 & x+y \end{bmatrix} = \begin{bmatrix} 8 & w \\ 0 & 6 \end{bmatrix}$ , entonces encuentra los valores de x, y, z y w.

Solución:

Como se da que las arrays son iguales, cada elemento en un índice dado en el lado izquierdo (LHS) debe ser igual al elemento en el mismo índice en el lado derecho (RHS).

De este modo,

a ₁₁ : xy = 8 ……………..(ecuación 1)

a ₁₂ : 4 = w ………………(ecuación 2)

a ₂₁ : z+6 = 0 …………..(ecuación 3)

a ₂₂ : x+y = 6 …………..(ecuación 4)

De (ecuación 2),

=> w = 4

Y de (ecuación 3),

=> z = -6

Ahora, podemos ver que (eq.1) y (eq.4) forman un sistema de ecuaciones que comprende las variables x e y.

De (ecuación 1),

=> x = 8/año

Sustituye (x=8/y) en (eq.4):

=> y + (8/y) = 6

=> y ² – 6y +8 = 0

Resolviendo la ecuación anterior,

=> y ² – 4y – 2y + 8 = 0

=> y( y-4 ) -2( y-4 ) = 0

=> (y – 2)(y – 4) = 0

=> y = 2 o 4

Sustituir en (ec.1):

=> cuando x=2, y=4 y cuando x=4, y=2 .

Así, (x,y) = (2,4) o (4,2) y z = -6 y w = 4.

Pregunta 17(i): Dé un ejemplo de una array fila que también sea una array columna.

Solución:

Sabemos que el orden de una array de filas se puede escribir como 1xn (1 fila con n elementos).

Y de manera similar, el orden de una array columna es mx1.

Entonces, una array fila que también es una array columna debe ser del orden (1×1) .

Como ejemplo, podemos tomar la array: $\begin{bmatrix} 1 \end{bmatrix}$

Pregunta 17(ii): Dé un ejemplo de una array diagonal que no sea escalar.

Solución:

En una array diagonal, solo los elementos diagonales poseen valores distintos de cero. Así, para una array diagonal de nxn, a _ii ≠ 0, para 1≤ i ≤ n.

Y una array escalar es una array diagonal, tal que todos los elementos de la diagonal son iguales.

Así, una array que es diagonal pero no escalar es:

$\begin{bmatrix} 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 3 \end{bmatrix}$

Pregunta 17(iii): Dé un ejemplo de una array triangular.

Solución:

Una array triangular es una array cuadrada, y se llena de tal manera que, el triángulo sobre la diagonal principal no es cero (triangular superior) o el triángulo debajo de la diagonal no es cero (triangular inferior) .

Así, un ejemplo sería: $\begin{bmatrix} 1 & 2 & 3\\ 0 & 1 & 4\\ 0 & 0 & 1 \end{bmatrix}$

Pregunta 18: La cifra de ventas de dos concesionarios de automóviles durante enero de 2013 mostró que el concesionario A vendió 5 automóviles de lujo, 3 premium y 4 estándar, mientras que el concesionario B vendió 7 automóviles de lujo, 2 premium y 3 estándar. Las ventas totales durante el mes de enero a febrero revelaron que el concesionario A vendió 8 autos de lujo, 7 premium y 6 estándar. En el mismo período de 2 meses, el concesionario B vendió 10 autos de lujo, 5 premium y 7 estándar. Escriba arrays de 2 × 3 que resuman los datos de ventas de enero y el período de 2 meses para cada distribuidor.

Solución:

Los datos anteriores se pueden representar en forma de tablas:

Para enero de 2013,

De lujo De primera calidad Estándar

Concesionario A 5 3 4

Concesionario B 7 2 3

Para enero a febrero,

De lujo De primera calidad Estándar

Concesionario A 8 7 6

Concesionario B 10 5 7

Así, las dos arrays son: $\begin{bmatrix} 5 & 3 & 4\\ 7 & 2 & 3 \end{bmatrix}$ y $\begin{bmatrix} 8 & 7 & 6\\ 10 & 5 & 7 \end{bmatrix}$

Pregunta 19: ¿Para qué valor de x e y son iguales las siguientes arrays?

A= 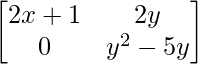$\begin{bmatrix} 2x+1 & 2y \\ 0 & y^2-5y \end{bmatrix}$ y B = $\begin{bmatrix} x+3 & y^2+2 \\ 0 & -6 \end{bmatrix}$

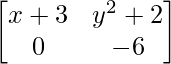
Solución:

Como se da que las arrays son iguales, cada elemento en un índice dado en el lado izquierdo (LHS) debe ser igual al elemento en el mismo índice en el lado derecho (RHS).

De este modo,

a ₁₁ : 2x+1 = x+3 …………(ecuación 1)

a ₁₂ : 2y = y ² +2 ……………(ecuación 2)

a ₂₁ : 0 = 0 …………………….(ecuación 3)

a ₂₂ : y ² -5y = -6 …………..(ecuación 4)

De (ecuación 1),

=> 2x-x = 3-1

=> x=2

Tomando (eq.2), se puede reescribir como,

=> y ² -2y+2 = 0

=> y = $\dfrac {2 \pm \sqrt{4-8}} {2}$

=> y = -1 ± i (Sin soluciones reales)

Tomando (eq.4), se puede reescribir como,

=> y ² – 5y +6 = 0

Resolviendo la ecuación,

=> y ² – 2y – 3y +6 = 0

=> y( y-2 ) -3( y-2 ) = 0

=> ( y-2 )( y-3 ) = 0

=> y = 2 o 3

Como los valores de y son inconsistentes, podemos decir que las arrays anteriores no son iguales para ningún par (x, y).

Pregunta 20. Encuentra los valores de x e y si 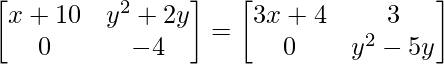$\begin{bmatrix} x+10 & y^2+2y\\ 0 & -4 \end{bmatrix} = \begin{bmatrix} 3x+4 & 3\\ 0 & y^2-5y \end{bmatrix}$ .

Solución:

Como se da que las arrays son iguales, cada elemento en un índice dado en el lado izquierdo (LHS) debe ser igual al elemento en el mismo índice en el lado derecho (RHS).

De este modo,

a ₁₁ : x+10 = 3x+4 …………(ecuación 1)

a ₁₂ : y ² +2y = 3 ……………(ecuación 2)

a ₂₁ : 0 = 0 ……………………..(ecuación 3)

a ₂₂ : y ² -5y = -4 …………..(ecuación 4)

De (ecuación 1),

=> 2x = 6

=> x = 3

Tomando (eq.2), se puede reescribir como,

=> ^y2 +2y-3 = 0

=> y ² + 3y -y -3 = 0

=> y( y+3 ) -1( y+3 ) = 0

=> ( y+3 )( y-1 ) = 0

=> y = -3 o 1

Tomando (eq.3), se puede reescribir como,

=> y ² -5y+4 = 0

=> y ² -4y -y +4 =0

=> y( y-4 ) -1( y-4 ) = 0

=> ( y-4 )( y-1 ) = 0

=> y = 4 o 1

El valor de y que puede satisfacer tanto (eq.2) como (eq.3) es 1.

=> y=1

Así, x=3 ey=1.

Pregunta 21. Encuentra los valores de a y b si A = B , donde A= 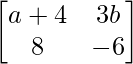$\begin{bmatrix} a+4 & 3b\\ 8 & -6 \end{bmatrix}$ , B= $\begin{bmatrix} 2a+2 & b^2+2\\ 8 & b^2-5b \end{bmatrix}$ .

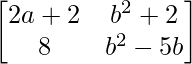Solución:

Como se da que las arrays son iguales, cada elemento en un índice dado en el lado izquierdo (LHS) debe ser igual al elemento en el mismo índice en el lado derecho (RHS).

De este modo,

a ₁₁ : a+4 = 2a+2 …………..(ecuación 1)

a ₁₂ : 3b = b ² +2 …………..(ecuación 2)

a ₂₁ : 8 = 8 ……………………..(ecuación 3)

a ₂₂ : -6 = b ² -5b ………….(ecuación 4)

De (ecuación 1),

=> un = 2

Tomando (eq.2), se puede reescribir como,

=> b ² -3b+2=0

=> ^{segundo 2} – 2b -b +2 = 0

=> b(b-2) -1(b-2) = 0

=> (b-2)(b-1) = 0

=> b=1 o 2

Tomando (eq.4) se puede reescribir como,

=> segundo ² -5b +6 = 0

=> ^{segundo 2} – 3b -2b + 6 = 0

=> b( b-3 ) -2( b-3 ) = 0

=> (b-3) (b-2) = 0

=> b = 2 o 3

Por lo tanto, b=2 puede satisfacer tanto (eq.2) como (eq.4).

=> segundo = 2

Así, a=2 yb=2.

Publicación traducida automáticamente

Artículo escrito por isha412k y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 RD Sharma Solutions- Capítulo 5 Álgebra de Arrays – Ejercicio 5.1 | conjunto 2

Pregunta 11: Encuentra x, y y z para que A = B, donde A= $\begin{bmatrix} x-2 & 3 & 2z\\ 18z & y+2 & 6z \end{bmatrix} = \begin{bmatrix} y & z & 6\\ 6y & x & 2y \end{bmatrix}$ .

Pregunta 12: Si $\begin{bmatrix} x & 3x-y\\ 2x+z & 3y-w \end{bmatrix} = \begin{bmatrix} 3 & 2\\ 4 & 7 \end{bmatrix}$ , encuentra x, y, z y w.

Pregunta 13: Si $\begin{bmatrix} x-y & z \\ 2x-y & w \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ 0 & 5 \end{bmatrix}$ , encuentra x, y, z y w.

Pregunta 14: Si $\begin{bmatrix} x+3 & z+4 & 2y-7\\ 4x+6 & a-1 & 0\\ b-3 & 3b & z+2c \end{bmatrix} = \begin{bmatrix} 0 & 6 & 3y-2\\ 2x & -3 & 2c+2\\ 2b+4 & -21 & 0 \end{bmatrix}$ . Obtenga los valores de a, b, c, x, y y z.

Pregunta 15: Si $\begin{bmatrix} 2x+1 & 5x \\ 0 & y^2+1 \end{bmatrix} = \begin{bmatrix} x+3 & 10 \\ 0 & 26 \end{bmatrix}$ , encuentra el valor de (x+y).

Pregunta 16: Si $\begin{bmatrix} xy & 4 \\ z+6 & x+y \end{bmatrix} = \begin{bmatrix} 8 & w \\ 0 & 6 \end{bmatrix}$ , entonces encuentra los valores de x, y, z y w.

Pregunta 17(i): Dé un ejemplo de una array fila que también sea una array columna.

Pregunta 17(ii): Dé un ejemplo de una array diagonal que no sea escalar.

Pregunta 17(iii): Dé un ejemplo de una array triangular.

Pregunta 19: ¿Para qué valor de x e y son iguales las siguientes arrays?

A= $\begin{bmatrix} 2x+1 & 2y \\ 0 & y^2-5y \end{bmatrix}$ y B = $\begin{bmatrix} x+3 & y^2+2 \\ 0 & -6 \end{bmatrix}$

Pregunta 20. Encuentra los valores de x e y si $\begin{bmatrix} x+10 & y^2+2y\\ 0 & -4 \end{bmatrix} = \begin{bmatrix} 3x+4 & 3\\ 0 & y^2-5y \end{bmatrix}$ .

Pregunta 21. Encuentra los valores de a y b si A = B , donde A= $\begin{bmatrix} a+4 & 3b\\ 8 & -6 \end{bmatrix}$ , B= $\begin{bmatrix} 2a+2 & b^2+2\\ 8 & b^2-5b \end{bmatrix}$ .

Deja una respuesta Cancelar la respuesta

Pregunta 11: Encuentra x, y y z para que A = B, donde A= .

Pregunta 12: Si , encuentra x, y, z y w.

Pregunta 13: Si , encuentra x, y, z y w.

Pregunta 14: Si . Obtenga los valores de a, b, c, x, y y z.

Pregunta 15: Si , encuentra el valor de (x+y).

Pregunta 16: Si , entonces encuentra los valores de x, y, z y w.

Pregunta 17(i): Dé un ejemplo de una array fila que también sea una array columna.

Pregunta 17(ii): Dé un ejemplo de una array diagonal que no sea escalar.

Pregunta 17(iii): Dé un ejemplo de una array triangular.

Pregunta 19: ¿Para qué valor de x e y son iguales las siguientes arrays?

A= y B =

Pregunta 20. Encuentra los valores de x e y si .

Pregunta 21. Encuentra los valores de a y b si A = B , donde A= , B= .

Deja una respuesta Cancelar la respuesta

Pregunta 11: Encuentra x, y y z para que A = B, donde A= $\begin{bmatrix} x-2 & 3 & 2z\\ 18z & y+2 & 6z \end{bmatrix} = \begin{bmatrix} y & z & 6\\ 6y & x & 2y \end{bmatrix}$ .

Pregunta 12: Si $\begin{bmatrix} x & 3x-y\\ 2x+z & 3y-w \end{bmatrix} = \begin{bmatrix} 3 & 2\\ 4 & 7 \end{bmatrix}$ , encuentra x, y, z y w.

Pregunta 13: Si $\begin{bmatrix} x-y & z \\ 2x-y & w \end{bmatrix} = \begin{bmatrix} -1 & 4 \\ 0 & 5 \end{bmatrix}$ , encuentra x, y, z y w.

Pregunta 14: Si $\begin{bmatrix} x+3 & z+4 & 2y-7\\ 4x+6 & a-1 & 0\\ b-3 & 3b & z+2c \end{bmatrix} = \begin{bmatrix} 0 & 6 & 3y-2\\ 2x & -3 & 2c+2\\ 2b+4 & -21 & 0 \end{bmatrix}$ . Obtenga los valores de a, b, c, x, y y z.

Pregunta 15: Si $\begin{bmatrix} 2x+1 & 5x \\ 0 & y^2+1 \end{bmatrix} = \begin{bmatrix} x+3 & 10 \\ 0 & 26 \end{bmatrix}$ , encuentra el valor de (x+y).

Pregunta 16: Si $\begin{bmatrix} xy & 4 \\ z+6 & x+y \end{bmatrix} = \begin{bmatrix} 8 & w \\ 0 & 6 \end{bmatrix}$ , entonces encuentra los valores de x, y, z y w.

A= $\begin{bmatrix} 2x+1 & 2y \\ 0 & y^2-5y \end{bmatrix}$ y B = $\begin{bmatrix} x+3 & y^2+2 \\ 0 & -6 \end{bmatrix}$

Pregunta 20. Encuentra los valores de x e y si $\begin{bmatrix} x+10 & y^2+2y\\ 0 & -4 \end{bmatrix} = \begin{bmatrix} 3x+4 & 3\\ 0 & y^2-5y \end{bmatrix}$ .

Pregunta 21. Encuentra los valores de a y b si A = B , donde A= $\begin{bmatrix} a+4 & 3b\\ 8 & -6 \end{bmatrix}$ , B= $\begin{bmatrix} 2a+2 & b^2+2\\ 8 & b^2-5b \end{bmatrix}$ .