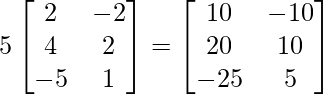
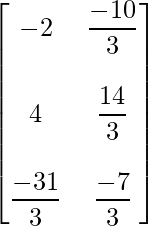
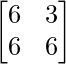
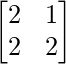
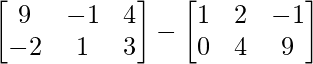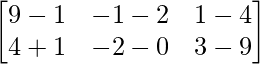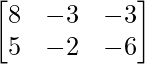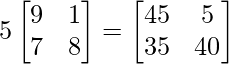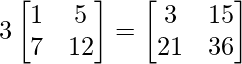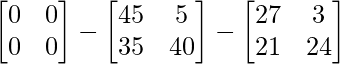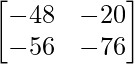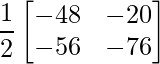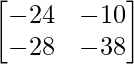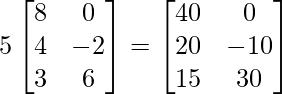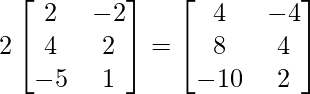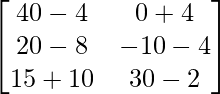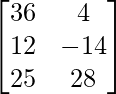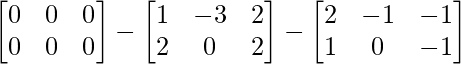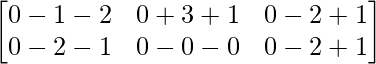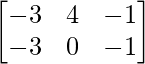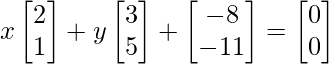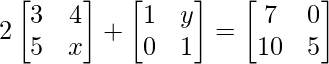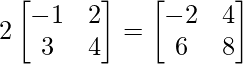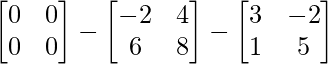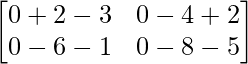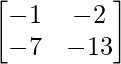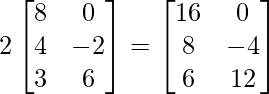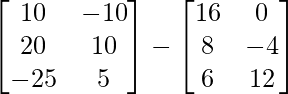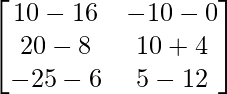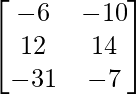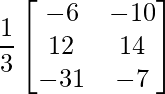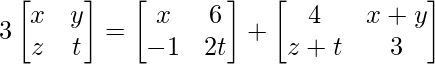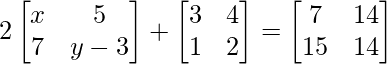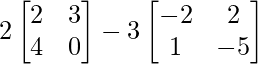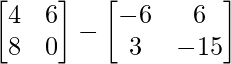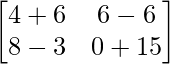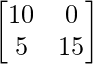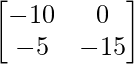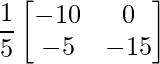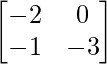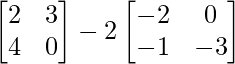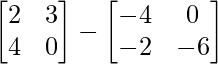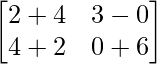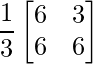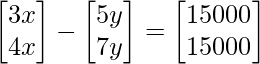Pregunta 11: Encuentre la array A, si 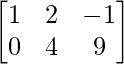 + A =
+ A = 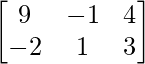 .
.
Solución:
Dado,
+ A =
.
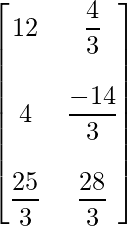
=> Un =
=> Un =
=> Un =
Pregunta 12: Si A = 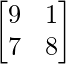 , B =
, B = 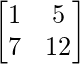 , encuentre C tal que 5A + 3B + 2C sea una array nula.
, encuentre C tal que 5A + 3B + 2C sea una array nula.
Solución:
Dado 5A + 3B + 2C =O, donde O es la array nula.
=> 2C = O – 5A – 3B.
=> 5A =
=> 3B =
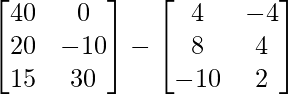
=> 2C =
=> 2C =
=> 2C =
=> C =
=> C =
Pregunta 13: Si A = 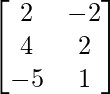 , B =
, B = 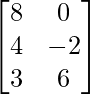 , encuentre la array X tal que 2A + 3X = 5B.
, encuentre la array X tal que 2A + 3X = 5B.
Solución:
Dado 2A + 3X = 5B.
=> 3X = 5B – 2A.
=> 5B =
=> 2A =
=> 3X =
=> 3X =
=> 3X =
=> X =
=> X =
Pregunta 14: Si A = 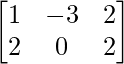 y B =
y B = 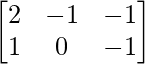 , encuentre la array C tal que A + B + C sea una array cero.
, encuentre la array C tal que A + B + C sea una array cero.
Solución:
Dado que A + B + C = O, donde O es una array nula.
=> C = O – A – B.
=> C =
=> C =
=> C =
Pregunta 15(i): Encuentre x, y que satisfagan la ecuación matricial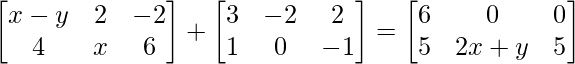
Solución:
Dado que,
Podemos llegar a 2 ecuaciones de la ecuación matricial anterior.
=> x – y + 3 = 6
=> x – y = 3 ……(ecuación 1)
=> x + 0 = 2x + y
=> -x = y ……….(ecuación 2)
Resolviendo (eq.1) y (eq.2) para x e y.
=> 2x = 3
=> x = 3/2
Sustituir x en (ecuación 2)
=> y = -3/2
Pregunta 15(ii): Encuentre x, y y z que satisfagan la ecuación matricial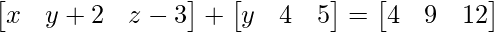
Solución:
Dado que,
=>
=>
Podemos llegar a 3 ecuaciones de la ecuación matricial anterior.
=> x + y = 4 ……(ecuación 1)
=> y + 6 = 9 ……(ecuación 2)
=> z + 2 = 12 ….(ecuación 3)
De (ecuación 2),
=> y = 9 – 6
=> y = 3
De (ecuación 3),
=> z = 12 – 2
=> z = 10
Sustituir el valor de y en (eq.1),
=> x + 3 = 4
=> x = 4 – 3
=> x = 1
Pregunta 15(iii): Encuentre x e y que satisfagan la ecuación matricial 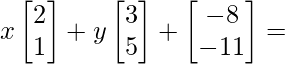 O.
O.
Solución:
Dado que,
Podemos llegar a 2 ecuaciones de la ecuación matricial anterior.
=> 2x + 3y – 8 = 0
=> 2x + 3y = 8 …….(ecuación 1)
=> x + 5y -11 = 0
=> x + 5y = 11 …….(ecuación 2)
Resolviendo para x e y , (eq.1) – 2.(eq.2),
=> 2x -2x + 3y – 10y = 8 – 22
=> -7 años = -14
=> y = 2
Sustituir y en (ecuación 2),
=> x + 5(2) = 11
=> x = 11 – 10
=> x = 1
Pregunta 16: Si 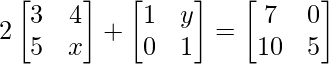 , encuentra x e y.
, encuentra x e y.
Solución:
Dado que,
Podemos llegar a 2 ecuaciones de la ecuación matricial anterior.
=> 2x + 1 = 5…….(ecuación 1)
=> 8 + y = 0……..(ecuación 2)
Resolviendo para x,
=> 2x = 5 – 1
=> 2x = 4
=> x = 2
Resolviendo para y,
=> y = -8
Pregunta 17: Encuentra el valor de 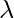 , un escalar distinto de cero, si
, un escalar distinto de cero, si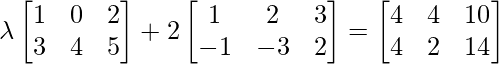
Solución:
Dado que,
=> Podemos llegar a varias ecuaciones para resolver,
sin embargo, tomemos una.
=>
=>
Si sustituimos
, en la array vemos que la ecuación se mantiene constante.
Por lo tanto,
.
Pregunta 18(i): Encuentre una array X tal que 2A + B + X = O, donde A = 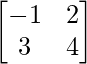 , B =
, B = 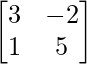 .
.
Solución:
Dado que, 2A + B + X = O.
=> 2A =
=> X = O-2A-B
=> X =
=> X =
=> X =
Pregunta 18(ii): Si A = 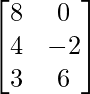 y B =
y B = 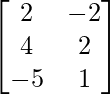 , entonces encuentre la array X de orden 3×2 tal que 2A + 3X = 5B.
, entonces encuentre la array X de orden 3×2 tal que 2A + 3X = 5B.
Solución:
Dado que 2A + 3X = 5B.
=> 3X = 5B – 2A.
=> 5B =
=> 2A =
=> 3X =
=> 3X =
=> 3X =
=> X =
=> X =
Pregunta 19(i): Encuentre x, y, z y t, si 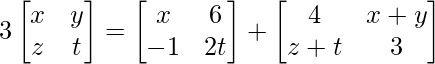 .
.
Solución:
Dado que,
Podemos llegar a 4 ecuaciones diferentes a partir de la ecuación matricial anterior,
=> 3x = x + 4 …………(ecuación 1)
=> 3y = 6 + x + y ….(ecuación 2)
=> 3z = -1 + z + t …(ecuación 3)
=> 3t = 2t + 3 ………..(ecuación 4)
De (ecuación 1),
=> 2x = 4
=> x = 2
Sustituir x=2 en (ecuación 2),
=> 3y = 6 + 2 + y
=> 2 años = 8
=> y = 4
De (ecuación 4),
=> t = 3
Sustituir t=3 en (ecuación 3),
=> 3z = -1 + z + 3
=> 2z = 2
=> z = 1
Pregunta 19(ii): Encuentre x, y, z y t, si 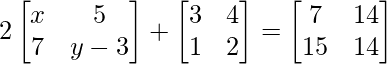 .
.
Solución:
Dado que,
Podemos llegar a 2 ecuaciones de la ecuación matricial anterior,
=> 2x + 3 = 7 ………………..(ecuación 1)
=> 2 (y – 3) + 2 = 14 ….(ecuación 2)
De (ecuación 1),
=> 2x = 7 – 3
=> 2x = 4
=> x = 2
De (ecuación 2),
=> 2 años – 6 + 2 = 14
=> 2 años = 14 + 4
=> 2 años = 18
=> y = 9
Pregunta 20: Si X e Y son arrays de 2×2, entonces resuelva las siguientes ecuaciones matriciales para X e Y, 2X + 3Y =  , 3X + 2Y =
, 3X + 2Y = 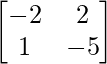 .
.
Solución:
Sea 2X + 3Y =
ser (ecuación 1) y sea 3X + 2Y =
, ser (ecuación 2) .
=> 2(2X + 3Y) – 3(3X + 2Y) = 4X + 6Y – 9X – 6Y = -5X.
=> -5X =
=> -5X =
=> -5X =
=> -5X =
=> 5X =
=> X =
=> X =
Sustituir la array X en (eq.1),
=> 3 años =
=> 3 años =
=> 3 años =
=> 3 años =
=> Y =
=> Y =
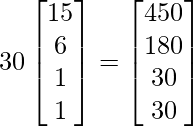
Pregunta 21: En cierta ciudad hay 30 colegios. Cada colegio tiene 15 peones, 6 empleados, 1 mecanógrafo y 1 oficial de sección. Exprese la información dada como una array de columna. Usando la multiplicación escalar, encuentre el número total de puestos de cada tipo en todas las universidades.
Solución:
Deje que los diferentes puestos en cada colegio se representen como:
Ahora el total de publicaciones se calculará de la siguiente manera:
Pregunta 22: Los ingresos mensuales de Aryan y Babban están en una proporción de 3 : 4 y sus gastos mensuales están en una proporción de 5 : 7. Si cada uno ahorra 15000 por mes, encuentre sus ingresos mensuales utilizando el método matricial.
Solución:
El problema se puede resolver considerando dos arrays, una para gastos y otra para ingresos.
=> La array de ingresos es:
donde x es una constante.
=> La array de gastos es:
donde y es una constante.
=>
Llegamos a 2 ecuaciones de la ecuación matricial anterior.
=> 3x – 5y = 15000……..(ecuación 1)
=> 4x – 7y = 15000……..(ecuación 2)
Resolviendo para y por 4(eq.1) – 3(eq.2),
=> 12x – 20y – 12x + 21y = 4(15000) – 3(15000)
=> y = 15000
Sustituir el valor de y en (eq.1),
=> 3x = 15000 + 5(15000)
=> 3x = 15000 + 75000
=> 3x = 90000
=> x = 30000
=> Sus ingresos y gastos son,
=> 3x = 3(30000) = 90000 y 5y = 5(15000) = 75000
=> 4x = 4(30000) = 120000 y 7y = 7(15000) = 105000