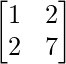
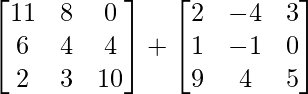
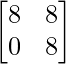
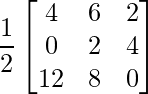
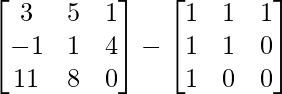
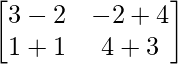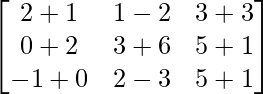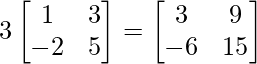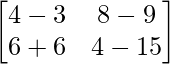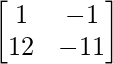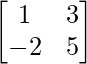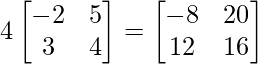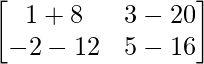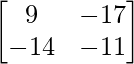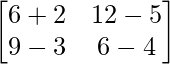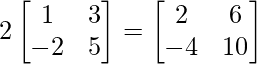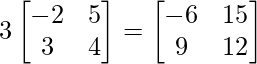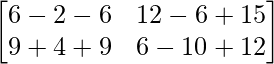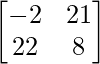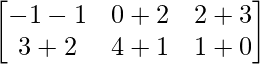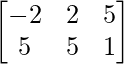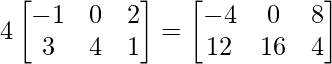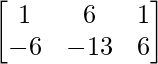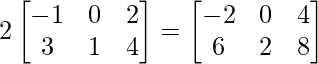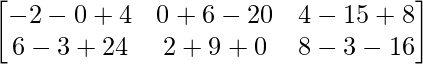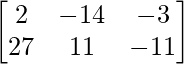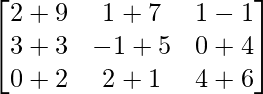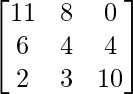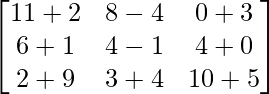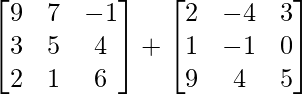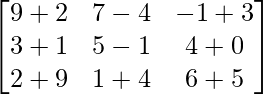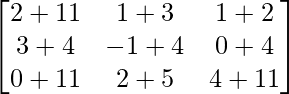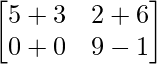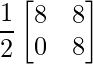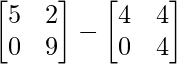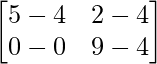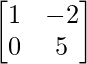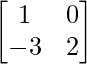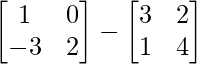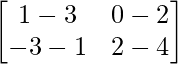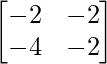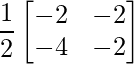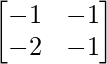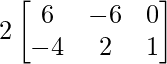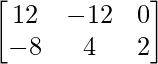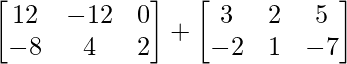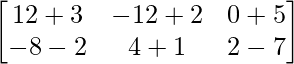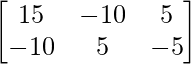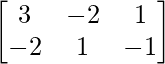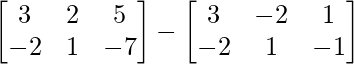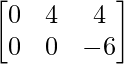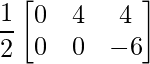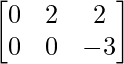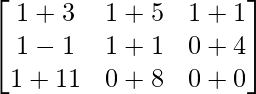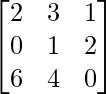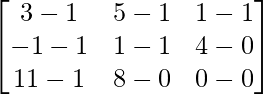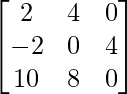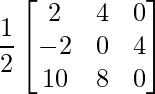Pregunta 1(i): Calcule la siguiente suma: 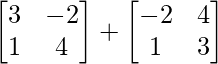 .
.
Solución:
Como las arrays son de las mismas dimensiones, podemos sumarlas para obtener una array de las mismas dimensiones que es 2×2.
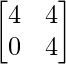
=>
=>
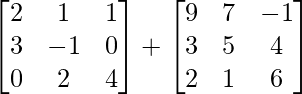
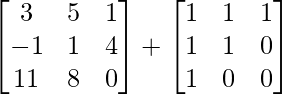
Pregunta 1(ii): Calcular la siguiente suma: 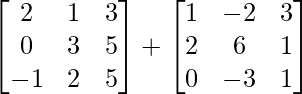 .
.
Solución:
Como las arrays son de las mismas dimensiones, podemos sumarlas para obtener una array de las mismas dimensiones que es 3×3.
=>
=>
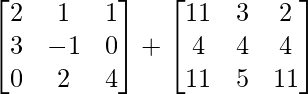
Pregunta 2: Sean A = 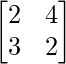 , B =
, B = 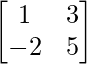 y C =
y C = 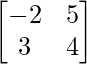 . Encuentre cada uno de los siguientes:
. Encuentre cada uno de los siguientes:
(yo): 2A – 3B
Solución:
Tanto las arrays A como B son del mismo orden, que es 2 × 2, por lo que se puede realizar la operación.
=> 2A =
=> 3B =
=> 2A – 3B =
=> 2A – 3B =
(ii): B-4C
Solución:
Tanto las arrays B como C son del mismo orden, que es 2×2, por lo que se puede realizar la operación.
=> segundo =
=> 4C =
=> B-4C =
=> B-4C =
(iii): 3A-C
Solución:
Tanto las arrays A como C son del mismo orden, que es 2×2, por lo que se puede realizar la operación.
=> 3A =
=> C =
=> 3A-C =
=> 3A-C =
(iv): 3A -2B + 3C
Solución:
Las arrays A, B y C son del mismo orden que es 2×2, por lo que se puede realizar la operación.
=> 3A =
=> 2B =
=> 3C =
=> 3A – 2B + 3C =
=> 3A – 2B + 3C =
Pregunta 3: Si A =  , B =
, B = 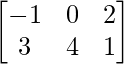 , C =
, C = 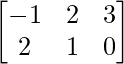 , encuentra:
, encuentra:
(i): A + B y B + C
Solución:
A y B no se pueden sumar ya que el orden de A es 2×2, que es diferente del orden de B, que es 2×3.
B+C se puede calcular y se resuelve de la siguiente manera:
=> B + C =
=> B + C =
(ii): 2B + 3A y 3C – 4B
Solución:
A y B no se pueden sumar ya que el orden de A es 2 × 2, que es diferente del orden de B, que es 2 × 3, y por lo tanto 2B + 3A no se puede calcular.
3C – 4B se puede calcular y se resuelve de la siguiente manera:
=> 3C =
=> 4B =
=> 3C – 4B =
=> 3C – 4B =
Pregunta 4: Sean A = 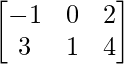 , B =
, B = 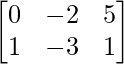 y C =
y C = 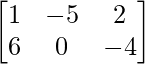 . Calcule 2A – 3B + 4C.
. Calcule 2A – 3B + 4C.
Solución:
El resultado se puede calcular ya que A, B y C son del mismo orden, que es 2×3.
=> 2A =
=> 3B =
=> 4C =
=> 2A – 3B + 4C =
=> 2A – 3B + 4C =
Pregunta 5: Si A =diag(2, -5, 9), B = diag(1, 1, -4) y C = diag(-6, 3, 4), encuentre:
(yo): A – 2B
Solución:
En la pregunta dada, A y B son arrays diagonales del orden de 3 × 3, por lo tanto, los únicos elementos distintos de cero están presentes en la diagonal.
=> A = diag(2, -5, 9)
=> 2B = 2. diagnóstico(1, 1, -4) = diagnóstico(2, 2, -8)
=> A – 2B = diag(2-2, -5-2, 9+8)
=> A – 2B = diagnóstico (0, -7, 17)
(ii): B + C – 2A
Solución:
En la pregunta dada, A, B y C son arrays diagonales del orden de 3 × 3, por lo que los únicos elementos distintos de cero están presentes en la diagonal.
=> B = diag(1, 1, -4)
=> C = diag(-6, 3, 4)
=> 2A = 2. diagnóstico(2, -5, 9) = diagnóstico(4, -10, 18)
=> B + C – 2A = diag(1-6-4, 1+3+10, -4+4-18)
=> B + C – 2A = diag(-9, 14, -18)
(iii): 2A + 3B – 5C
Solución:
En la pregunta dada, A, B y C son arrays diagonales del orden de 3 × 3, por lo que los únicos elementos distintos de cero están presentes en la diagonal.
=> 2A = 2. diagnóstico(2, -5, 9) = diagnóstico(4, -10, 18)
=> 3B = 3. diagnóstico(1, 1, -4) = diagnóstico(3, 3, -12)
=> 5C = 5. diag(-6, 3, 4) = diag(-30, 15, 20)
=> 2A + 3B – 5C = diagnóstico (4+3+30, -10+3-15, 18-12-20)
=> 2A + 3B – 5C = diag(37, -22, -14)
Pregunta 6: Dadas las arrays A = 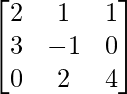 , B =
, B = 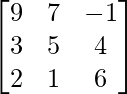 y C =
y C =  . Verifica que (A + B) + C = A + (B + C).
. Verifica que (A + B) + C = A + (B + C).
Solución:
Dado LHS:
=> (A + B) =
=> (A + B) =
=> (A + B) =
=> (A + B) + C =
=> (A + B) + C =
=> (A + B) + C =
Dado el lado derecho:
=> (B + C) =
=> (B + C) =
=> (B + C) =
=> A + (B + C) =
=> A + (B + C) =
=> A + (B + C) =
Por lo tanto, se ha verificado RHS = LHS.
Pregunta 7: Encuentra las arrays X e Y, si X + Y = 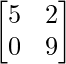 y X – Y =
y X – Y = 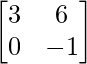 .
.
Solución:
Sabemos que (X + Y) + (X – Y) = 2X.
=> (X + Y) + (X – Y) =
=> 2X =
=> 2X =
=> X =
=> X =
Ahora Y = (X + Y) – X
=> Y =
=> Y =
=> Y =
Pregunta 8: Encuentra X, si Y =  y 2X + Y =
y 2X + Y = 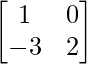 .
.
Solución:
Dado 2X + Y =
=> 2X +
=
=> 2X =
=> 2X =
=> 2X =
=> X =
=> X =
Pregunta 9: Encuentra las arrays X e Y, si 2X – Y = 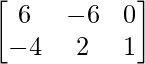 y X + 2Y =
y X + 2Y =  .
.
Solución:
Sabemos que 2 (2X – Y) + (X + 2Y) = 4X – 2Y + X + 2Y = 5X.
=> 2 (2X – Y) =
=> 2 (2X-Y) =
=> 2 (2X – Y) + (X + 2Y) =
=> 5X =
=> 5X =
=> X =
=> X =
Como (X + 2Y) =
=>
=> 2 años =
=> 2 años =
=> Y =
=> Y =
Pregunta 10: Si X – Y = 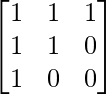 y X + Y =
y X + Y = 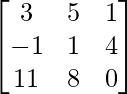 , encuentra X e Y.
, encuentra X e Y.
Solución:
Sabemos que (X + Y) + (X – Y) = 2X.
=> 2X =
=> 2X =
=> 2X =
=> X =
=> X =
También (X + Y) – (X -Y) = 2Y.
=> 2 años =
=> 2 años =
=> 2 años =
=> Y =
=> Y =