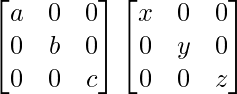
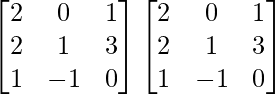
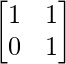
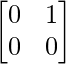
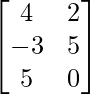
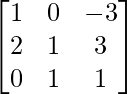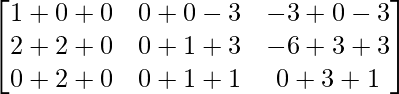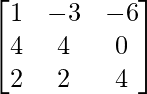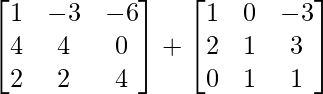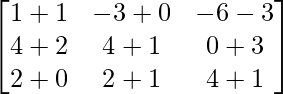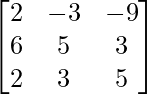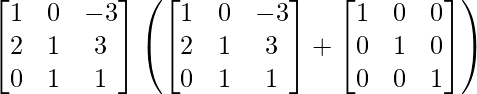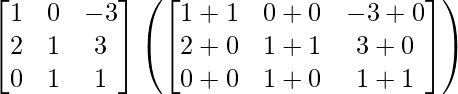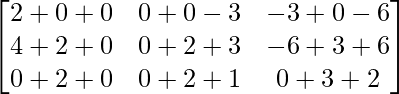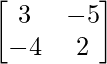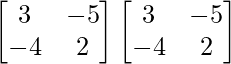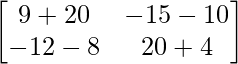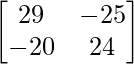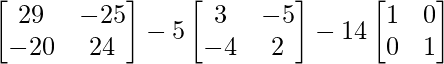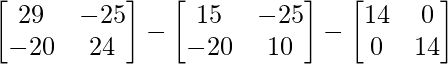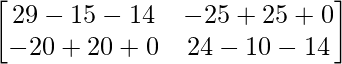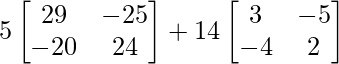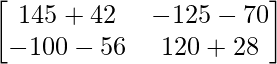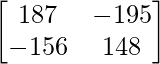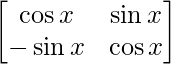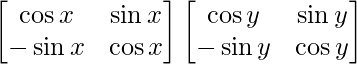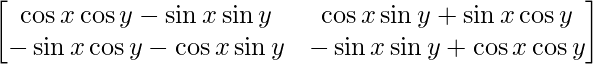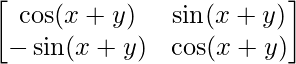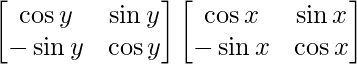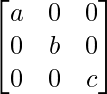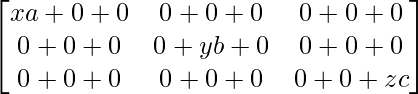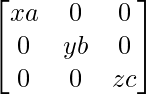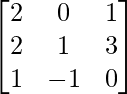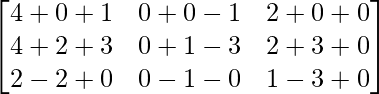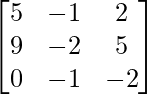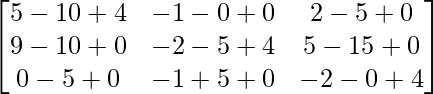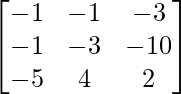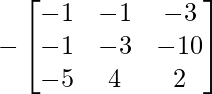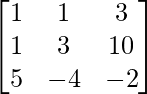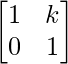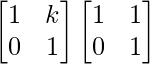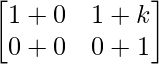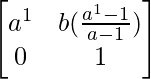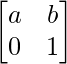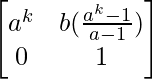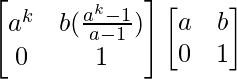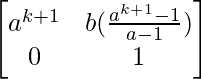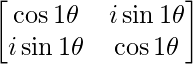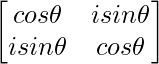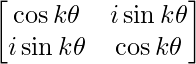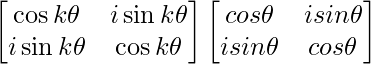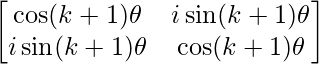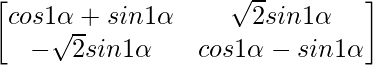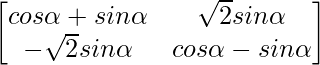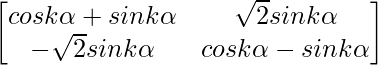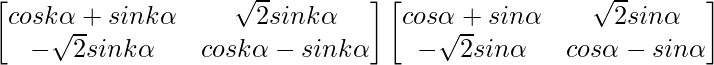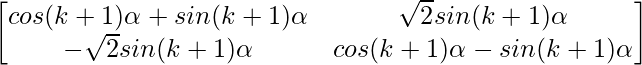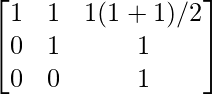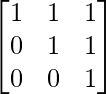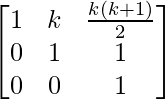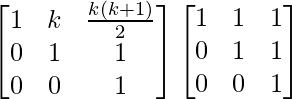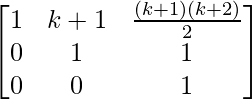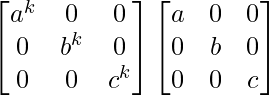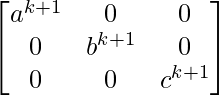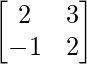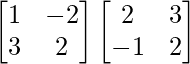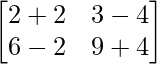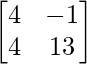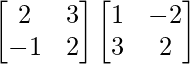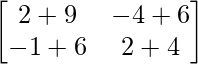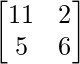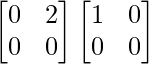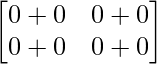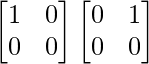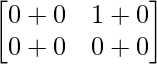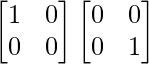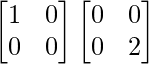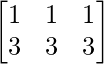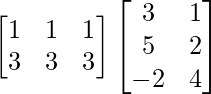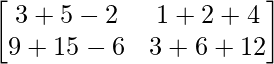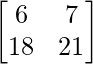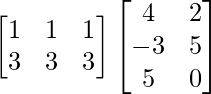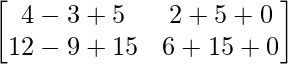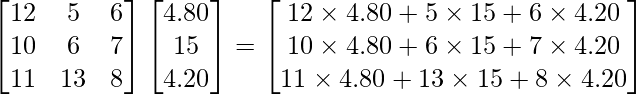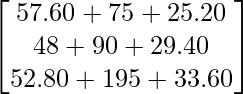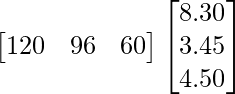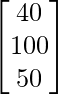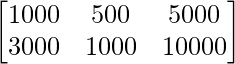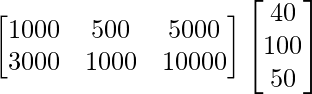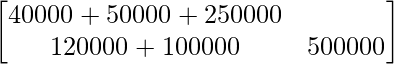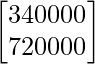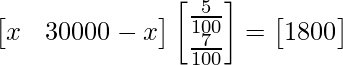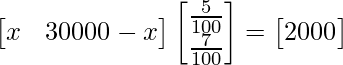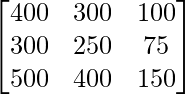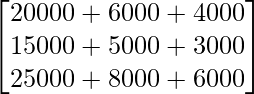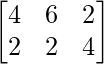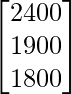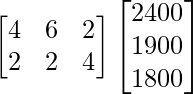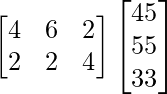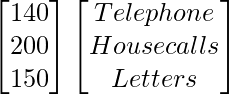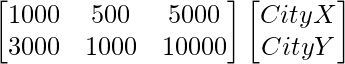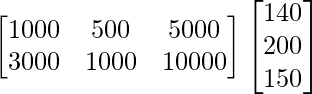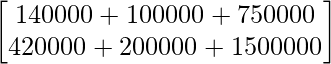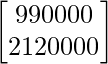Pregunta 52. Si A = 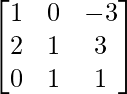 , entonces verifica que A 2 + A = A (A + I), donde I es la array identidad.
, entonces verifica que A 2 + A = A (A + I), donde I es la array identidad.
Solución:
Tenemos,
un =
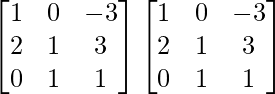
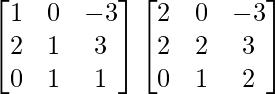
un 2 =
=
=
IZQ = A 2 + A
=
=
=
RHS = A (A + I)
=
=
=
=
=
= LHS
Por lo tanto probado.
Pregunta 53. Si A =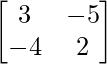 , entonces encuentra A 2 – 5A – 14I. Por lo tanto, obtenga A 3 .
, entonces encuentra A 2 – 5A – 14I. Por lo tanto, obtenga A 3 .
Solución:
Tenemos,
un =
un 2 =
=
=
Entonces, A 2 – 5A – 14I =
=
=
=
= 0
Ahora, como A 2 – 5A – 14I = 0
=> A2 = 5A + 14I
=> UN 2 UN = UN (5A + 14I)
=> A 3 = 5A 2 + 14 AI
=> A 3 = 5 A 2 + 14 A
=> Un 3 =
=> Un 3 =
=> Un 3 =
Pregunta 54. Demuestre lo siguiente:
(i) Si P(x) = 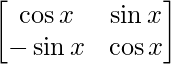 , entonces demuestre que P(x) P(y) = P(x+y) = P(y) P(x).
, entonces demuestre que P(x) P(y) = P(x+y) = P(y) P(x).
Solución:
Tenemos,
P(x) =
Ahora, P(x) P(y) =
=
=
= P(x+y)
Además, P(y) P(x) =
=
=
= P(x+y)
Por lo tanto, P(x) P(y) = P(x+y) = P(y) P(x).
Por lo tanto probado.
(ii) Si P = 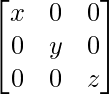 y Q =
y Q = 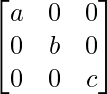 , demuestre que PQ =
, demuestre que PQ = 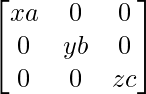 = QP.
= QP.
Solución:
Tenemos,
P =
y Q =
PQ =
=
=
QP =
=
=
Por lo tanto, PQ =
= QP.
Por lo tanto probado.
Pregunta 55. Si A = 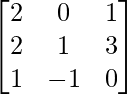 , encuentra A 2 – 5A + 4I y encuentra una array X tal que A 2 – 5A + 4I + X = 0.
, encuentra A 2 – 5A + 4I y encuentra una array X tal que A 2 – 5A + 4I + X = 0.
Solución:
Tenemos,
un =
un 2 =
=
=
Entonces, A 2 – 5A + 4I =
=
=
Si A 2 – 5A + 4I + X = 0, entonces
=> X = – (A 2 – 5A + 4I)
=> X =
=> X =
Pregunta 56. Si A = 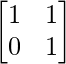 , demuestre que A =
, demuestre que A = 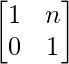 , para todo entero positivo n.
, para todo entero positivo n.
Solución:
Usando el principio de inducción matemática, obtenemos
Paso 1: Para n = 1, tenemos
un 1 =
Entonces, el resultado es verdadero para n = 1.
Paso 2: Suponiendo que el resultado es verdadero para n = k, tenemos
un k =
Paso 3: Para n = k + 1, tenemos
UN k+1 = UN k UN
=
=
Entonces, el resultado también es cierto para n = k+1.
Por lo tanto, el resultado anterior es cierto para todo entero positivo n.
Por lo tanto probado.
Pregunta 57. Si A = 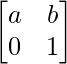 , demuestre que A n =
, demuestre que A n = 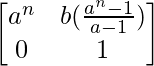 , para todo entero positivo n.
, para todo entero positivo n.
Solución:
Usando el principio de inducción matemática, obtenemos
Paso 1: Para n = 1, tenemos
un 1 =
=
Entonces, el resultado es verdadero para n = 1.
Paso 2: Suponiendo que el resultado es verdadero para n = k, tenemos
un k =
Paso 3: Para n = k + 1, tenemos
UN k+1 = UN k UN
=
=
Entonces, el resultado también es cierto para n = k+1.
Por lo tanto, el resultado anterior es cierto para todo entero positivo n.
Por lo tanto probado.
Pregunta 58. Si A = 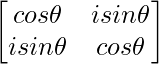 , demostrar por principio de inducción matemática que A n =
, demostrar por principio de inducción matemática que A n = 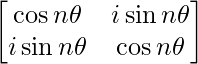 , para todo n ∈ N.
, para todo n ∈ N.
Solución:
Usando el principio de inducción matemática, obtenemos
Paso 1: Para n = 1, tenemos
un 1 =
=
Entonces, el resultado es verdadero para n = 1.
Paso 2: Suponiendo que el resultado es verdadero para n = k, tenemos
un k =
Paso 3: Para n = k + 1, tenemos
UN k+1 = UN k UN
=
=
Entonces, el resultado también es cierto para n = k+1.
Por lo tanto, el resultado anterior es cierto para todo entero positivo n.
Por lo tanto probado.
Pregunta 59. Si A = 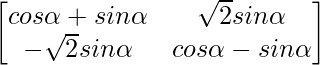 , demuestre que A n =
, demuestre que A n = 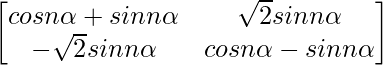 , para todo n ∈ N.
, para todo n ∈ N.
Solución:
Usando el principio de inducción matemática, obtenemos
Paso 1: Para n = 1, tenemos
un 1 =
=
Entonces, el resultado es verdadero para n = 1.
Paso 2: Suponiendo que el resultado es verdadero para n = k, tenemos
un k =
Paso 3: Para n = k + 1, tenemos
UN k+1 = UN k UN
=
=
Entonces, el resultado también es cierto para n = k+1.
Por lo tanto, el resultado anterior es cierto para todo entero positivo n.
Por lo tanto probado.
Pregunta 60. Si A = 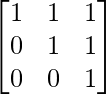 , probar por principio de inducción matemática que A n =
, probar por principio de inducción matemática que A n = 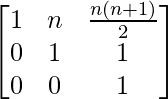 para todo entero positivo n.
para todo entero positivo n.
Solución:
Usando el principio de inducción matemática, obtenemos
Paso 1: Para n = 1, tenemos
un 1 =
=
Entonces, el resultado es verdadero para n = 1.
Paso 2: Suponiendo que el resultado es verdadero para n = k, tenemos
un k =
Paso 3: Para n = k + 1, tenemos
UN k+1 = UN k UN
=
=
Entonces, el resultado también es cierto para n = k+1.
Por lo tanto, el resultado anterior es cierto para todo entero positivo n.
Por lo tanto probado.
Pregunta 61. Si B, C son arrays cuadradas de n filas y si A = B + C, BC = CB, C 2 = 0, entonces demuestre que para todo n ∈ N, A n+1 = B n (B + (n +1)C).
Solución:
Se nos da,
A = B + C, BC = CB y C 2 = 0
=> UN 2 = (B + C) 2
=> UN 2 = B 2 + C 2 + 2 BC
=> A 2 = B 2 + 2 BC
=> UN 2 = segundo (segundo + 2C) . . . . (1)
Tenemos que demostrar que A n+1 = B n (B + (n+1)C), para n ∈ N
Usando el principio de inducción matemática, obtenemos
Paso 1: Para n = 1, tenemos
UN 1+1 = B 1 (B + (1+1)C)
UN 2 = B (B + 2C)
De (1) obtenemos que el resultado es cierto para n = 1.
Paso 2: Suponiendo que el resultado es verdadero para n = k, tenemos
UNk +1 = Bk (B + (k+1)C )
Paso 3: Para n = k + 1, tenemos
UN k+1+1 = UN k+2 = UN k UN 2
= B k-1 (B + kC) B (B + 2C)
= B k (B + kC) (B + 2C)
= B k (B 2 + 2BC+ k CB + 2kC 2 )
= B k (B 2 + 2BC+ k BC)
= B k B (B + (k+2)C)
= Bk+1 (B + (k+2)C)
Entonces, el resultado también es cierto para n = k+1.
Por lo tanto, el resultado anterior es cierto para todo entero positivo n.
Por lo tanto probado.
Pregunta 62. Si A = diag (a, b, c), demuestre que A n = diag (a n , b n , c n ), para todo entero positivo n.
Solución:
Usando el principio de inducción matemática, obtenemos
Paso 1: Para n = 1, tenemos
A 1 = diag (a 1 , b 1 , c 1 )
A = diag (a, b, c)
Entonces, el resultado es verdadero para n = 1.
Paso 2: Suponiendo que el resultado es verdadero para n = k, tenemos
UN k = diag (un k , segundo k , c k )
Paso 3: Para n = k + 1, tenemos
UN k+1 = UN k UN
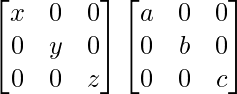
= diag (a k , b k , c k ) diag (a, b, c)
=
=
Entonces, el resultado también es cierto para n = k+1.
Por lo tanto, el resultado anterior es cierto para todo entero positivo n.
Por lo tanto probado.
Pregunta 63. Si A es una array cuadrada, probar por inducción matemática que (A T ) N = (A N ) T para todo n ∈ N.
Solución:
Usando el principio de inducción matemática, obtenemos
Paso 1: Para n = 1, tenemos
(UN T ) 1 = (UN 1 ) T
UNA T = UNA T
Entonces, el resultado es verdadero para n = 1.
Paso 2: Suponiendo que el resultado es verdadero para n = k, tenemos
(UN T ) K = (UN K ) T
Paso 3: Para n = k + 1, tenemos
(UN T ) K+1 = (UN T ) K (UN T ) 1
= (A K ) T (A 1 ) T
= ( AK+1 ) T
Entonces, el resultado también es cierto para n = k+1.
Por lo tanto, el resultado anterior es cierto para todo entero positivo n.
Por lo tanto probado.
Pregunta 64. Una array X tiene a + b filas y a + 2 columnas mientras que la array Y tiene b + 1 filas y a + 3 columnas. Ambas arrays XY e YX existen. Encuentre a y b. ¿Puedes decir que XY e YX son del mismo tipo? ¿Son iguales?
Solución:
Aquí X es de orden (a+b) × (a+2) e Y es de orden (b+1) × (a+3).
Si existe XY, obtenemos
=> un + 2 = segundo + 1 . . . . (1)
Y si existe YX, obtenemos
=> un + segundo = un + 3
=> segundo = 3
Poniendo esto en (1), tenemos
=> un + 2 = 3 + 1
=> un = 2
Dado que el orden de las arrays XY e YX no es el mismo, XY e YX no son del mismo tipo y son desiguales.
Pregunta 65. Da un ejemplo de arrays A y B tales que:
(i) AB ≠ BA
Solución:
Sean A =
y B =
AB =
=
=
Ahora BA =
=
=
Por lo tanto, AB ≠ BA.
(ii) AB = O pero A ≠ 0, B ≠ 0
Solución:
Sean A =
y B =
AB =
=
=
Entonces, AB = O pero A ≠ 0, B ≠ 0.
(iii) AB = O Pero BA ≠ O
Solución:
Sean A =
y B =
Aquí, AB = 0
Pero BA =
=
=
Entonces, AB = O pero BA ≠ O.
(iv) AB = AC pero B ≠ C, A ≠ 0
Solución:
Sean A =
, B =
y C =
AB =
=
=
y CA =
=
=
Entonces, AB = AC pero B ≠ C, A ≠ 0.
Pregunta 66. Sean A y B arrays cuadradas del mismo orden. ¿Se cumple (A + B) 2 = A 2 + 2AB + B 2 ? Si no, ¿por qué?
Solución:
Tenemos,
LHS = (A + B) 2
= (A + B) (A + B)
= A (A + B) + B (A + B)
= A 2 + AB + BA + B 2
Aquí AB ≠ BA como array no tiene propiedad conmutativa.
Por lo tanto, (A + B) 2 ≠ A 2 + 2AB + B 2 .
Pregunta 67. Si A y B son arrays cuadradas del mismo orden, explique por qué en general
(i) (A + B) 2 ≠ A 2 + 2AB + B 2
Solución:
Tenemos,
LHS = (A + B) 2
= (A + B) (A + B)
= A (A + B) + B (A + B)
= A 2 + AB + BA + B 2
Aquí AB ≠ BA como en general la array no tiene una propiedad conmutativa.
Por lo tanto, (A + B) 2 ≠ A 2 + 2AB + B 2 .
(ii) (A – B) 2 ≠ A 2 – 2AB + B 2
Solución:
Tenemos,
IZQ = (A – B) 2
= (A-B) (A-B)
= A (A – B) + B (A – B)
= A 2 – AB – BA + B 2
Aquí AB ≠ BA como en general la array no tiene una propiedad conmutativa.
Por lo tanto, (A – B) 2 ≠ A 2 – 2AB + B 2 .
(iii) (A + B) (A – B) ≠ A 2 – B 2
Solución:
Tenemos,
IZQ = (A + B) (A – B)
= A (A – B) + B (A – B)
= A 2 – AB + BA – B 2
Aquí AB ≠ BA como en general la array no tiene una propiedad conmutativa.
Por lo tanto, (A + B) (A – B) ≠ A 2 – B 2 .
Pregunta 68. Sean A y B arrays cuadradas del orden 3 × 3. ¿Es (AB) 2 = A 2 B 2 ? Dar razones.
Solución:
Sabemos, (AB) 2 = A 2 B 2 , solo si AB = BA
Si AB = BA, entonces
(AB) 2 = (AB) (AB)
Al usar la ley asociativa, obtenemos
= A (BA) B
= A (AB) B
= A 2 B 2
Por lo tanto probado.
Pregunta 69. Si A y B son arrays cuadradas del mismo orden tales que AB = BA, entonces demuestre que (A + B) 2 = A 2 + 2AB + B 2 .
Solución:
Nos dan, AB = BA.
LHS = (A + B) 2
= (A + B) (A + B)
= A (A + B) + B (A + B)
= A2 + AB + BA + B2
= A 2 + AB + BA + B 2
= A 2 + 2AB + B 2
= lado derecho
Por lo tanto probado.
Pregunta 70. Sean A = 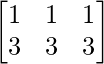 , B =
, B = 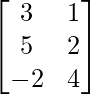 y C =
y C = 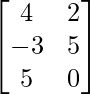 . Verifique que AB = AC aunque B ≠ C, A ≠ O.
. Verifique que AB = AC aunque B ≠ C, A ≠ O.
Solución:
Tenemos,
A =
, B =
y C =
IZQ = AB
=
=
=
RHS = CA
=
=
=
Por lo tanto, LHS = RHS
Por lo tanto probado.
Pregunta 71. Tres comerciantes A, B y C van a una tienda a comprar artículos de papelería. A compra 12 docenas de cuadernos, 5 docenas de bolígrafos y 6 docenas de lápices. B compra 10 docenas de cuadernos, 6 docenas de bolígrafos y 7 docenas de lápices. C compra 11 docenas de cuadernos, 13 docenas de bolígrafos y 8 docenas de lápices. Un cuaderno cuesta 40 paise, un bolígrafo cuesta Rs. 1,25 y un lápiz cuesta 35 paise. Utilice la multiplicación de arrays para calcular la factura de cada individuo.
Solución:
Costo de cuadernos por docena = (12 × 40) paise = Rs 4,80
Costo de bolígrafos por docena = (12 × 1,25) paise = Rs 15
Costo de lápices por docena = (12 × 35) paise = Rs 4,20
Entonces, obtenemos
=
=
Por lo tanto, las facturas de A, B y C son Rs 157,80, Rs 167,40 y Rs 281,40, respectivamente.
Pregunta 72. Las tiendas cooperativas de una escuela en particular tienen 10 docenas de libros de física, 8 docenas de libros de química y 5 docenas de libros de matemáticas. Sus precios de venta son Rs. 8,30 rupias 3,45 y Rs. 4,50 cada uno respectivamente. Halla la cantidad total que recibirá la tienda por vender todos los artículos.
Solución:
Las existencias de varios tipos de libros en la tienda se dan como,
Física Química Matemáticas
X =
El precio de venta de varios tipos de libros en la tienda es,
Y =
El monto total recibido por la tienda por la venta de todos los artículos será = XY
XY =
=
=
=
Por lo tanto, la cantidad total que recibirá la tienda por la venta de todos los artículos es de 1597,20 rupias.
Pregunta 73. En una elección de asamblea legislativa, una agrupación política contrató a una empresa de relaciones públicas para promocionar a sus candidatos de tres formas: teléfono, visitas domiciliarias y cartas. El costo por contacto (en paise) se da en la array A como
Costo por contacto
un =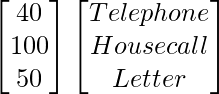
El número de contactos de cada tipo realizados en dos ciudades X e Y se da en la array B como
Teléfono Llamada a domicilio Carta
B =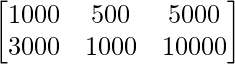
Encuentre la cantidad total gastada por el grupo en las dos ciudades X e Y.
Solución:
El costo por contacto (en paises) viene dado por
un =
El número de contactos de cada tipo realizados en las dos ciudades X e Y viene dado por
Teléfono Visitas a domicilio Carta
B =
La cantidad total gastada por el grupo en las dos ciudades X e Y viene dada por
AB =
=
=
Por lo tanto, la cantidad gastada en X = 3400 rupias y la cantidad gastada en Y = 7200 rupias.
Pregunta 74. Un fondo fiduciario tiene Rs 30000 que deben invertirse en dos tipos diferentes de bonos. El primer bono paga 5% de interés anual y el segundo bono paga 7% de interés anual. Usando la multiplicación de arrays, determine cómo dividir Rs 30000 entre los dos tipos de bonos. Si el fideicomiso debe obtener un interés total anual de
(i) 1800 rupias
Solución:
Supongamos que Rs x se invierten en el primer tipo de bono y Rs (30000 – x) se invierten en el segundo tipo de bono, entonces
A =
representa la inversión y la array y B =
representa la tasa de interés
Entonces, obtenemos
=>
=>
=>
=> 210000 – 2x = 180000
=> 2x = 30000
=> x = 15000
Por lo tanto, cantidad invertida en el primer bono = Rs 15000 y cantidad invertida en el segundo bono = Rs (30000 – 15000) = Rs 15000.
(ii) 2000 rupias
Solución:
Supongamos que Rs x se invierten en el primer tipo de bono y Rs (30000 – x) se invierten en el segundo tipo de bono, entonces
A =
representa la inversión y la array y B =
representa la tasa de interés
Entonces, obtenemos
=>
=>
=>
=> 210000 – 2x = 200000
=> 2x = 10000
=> x = 5000
Por lo tanto, cantidad invertida en el primer bono = Rs 5000 y cantidad invertida en el segundo bono = Rs (30000 – 5000) = Rs 25000.
Pregunta 75. Para promover la fabricación de baños para mujeres, una organización trató de generar conciencia a través de (i) visitas a domicilio (ii) cartas y (iii) anuncios. El costo de cada modo por intento se indica a continuación:
i. Rs. 50
ii. Rs. 20
iii. Rs. 40
El número de intentos realizados en tres aldeas X, Y y Z se dan a continuación:
| (i) | (ii) | (iii) | |
| X | 400 | 300 | 100 |
| Y | 300 | 250 | 75 |
| Z | 500 | 400 | 150 |
Encuentre el costo total incurrido por la organización para tres aldeas por separado, usando arrays.
Solución:
Sea A la array que muestra el número de intentos realizados en tres pueblos X, Y y Z.
un =
Y supongamos que B es una array que muestra el costo de cada modo por intento.
B =
AB =
=
=
Por lo tanto, el costo total incurrido por la organización para tres aldeas X, Y y Z es de 30 000, 23 000 y 39 000 respectivamente.
Pregunta 76. Hay 2 familias A y B. Hay 4 hombres, 6 mujeres y 2 niños en la familia A, y 2 hombres, 2 mujeres y 4 niños en la familia B. La cantidad diaria recomendada de calorías es 2400 para hombres, 1900 para mujeres, 1800 para niños y 45 gramos de proteínas para hombres, 55 gramos para mujeres y 33 gramos para niños. Representa la información anterior usando una array. Usando la multiplicación de arrays, calcule el requerimiento total de calorías y proteínas para cada una de las dos familias. ¿Qué conciencia puedes crear entre las personas sobre la dieta planificada a partir de esta pregunta?
Solución:
Sea X la array que muestra el número de miembros de la familia en la familia A y B.
X =
Y supongamos que Y es una array que muestra la cantidad diaria recomendada de calorías.
Y =
Y, Z sea una array que muestre la cantidad diaria recomendada de proteínas.
Z =
Ahora, el requerimiento total de calorías de las dos familias será mostrado por XY.
XY =
=
=
Además, el requerimiento total de proteínas de las dos familias se mostrará mediante XZ.
X Z =
=
=
Por lo tanto, el requerimiento total de calorías y proteínas para cada una de las dos familias es
.
Debemos llevar una dieta balanceada para mantenernos saludables.
Pregunta 77. En una elección parlamentaria, un partido político contrató a una empresa de relaciones públicas para promocionar a sus candidatos de tres maneras: teléfono, visitas a domicilio y cartas. El costo por contacto (en paisa) se da en la array A como
un =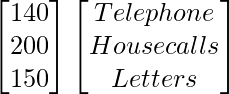
El número de contactos de cada tipo realizados en dos ciudades X e Y se da en la array B como
Teléfono Visitas a domicilio Cartas
B =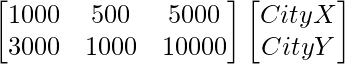
Encuentre la cantidad total gastada por el partido en las dos ciudades. ¿Qué se debe considerar antes de emitir su voto: la actividad de promoción del partido de sus actividades sociales?
Solución:
Sea A la array que muestra el costo por contacto (en paisa).
un =
Y, sea B una array que muestre el número de contactos de cada tipo realizados en dos ciudades X e Y.
Teléfono Visitas a domicilio Cartas
B =
Ahora, BA mostrará el monto total gastado por el partido en las dos ciudades.
AB =
=
=
Por lo tanto, la cantidad total gastada por el partido en las dos ciudades X e Y es 9900 y 21200 respectivamente.
Uno debe considerar las actividades sociales de un partido antes de emitir su voto a ese partido.
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA