Pregunta 1: Sean A =  y B =
y B = 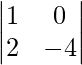 verificar que
verificar que
(i) (2A) T = 2A T
(ii) (A + B) T = A T + B T
(iii) (A – B) T = A T – B T
(iv) (AB) T = B T A T
Solución:
(i) Dado: A =
y B =
Asumir,
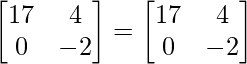
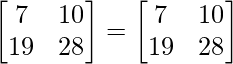
(2A) T = 2A T
Sustituye el valor de A
LHS = RHS
Por lo tanto, probado.
(ii) Dado: A =
y B =
Asumir,
(A+B) T = UN T + B T
LHS = RHS
Por lo tanto, probado.
(iii) Dado: A=
y B=
Asumir,
(A – segundo) T = UN T – segundo T
LHS = RHS
Por lo tanto, demostrado
(iv) Dado: A =
y B =
Asumir,
(AB) T = B T UN T
Por lo tanto, (AB) T = B T A T
Por lo tanto, probado.
Pregunta 2: A =  y B =
y B = 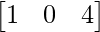 Verifique que (AB) T = B T A T
Verifique que (AB) T = B T A T
Solución :
Dado: A =
y B =
Asumir,
(AB) T = B T UN T
LHS = RHS
Por lo tanto probado
Pregunta 3: Sean A = 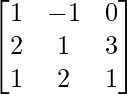 y B =
y B = 
Encuentre A T , B T y verifique que
(i) (A + B) T = A T + B T
(ii) (AB) T = B T A T
(iii) (2A) T = 2A T
Solución:
(i) Dado: A =
y B =
Asumir
(A + B) T = UN T + B T
LHS = RHS
Por lo tanto probado
(ii) Dado: A =
y B =
Asumir,
(AB) T = B T UN T
IZQ =DERECHA
Por lo tanto probado
(iii) Dado: A =
y B =
Asumir,
(2A) T = 2A T
LHS = RHS
Por lo tanto probado
Pregunta 4: si A =  , B =
, B = 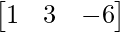 , verifica que (AB) T = B T A T
, verifica que (AB) T = B T A T
Solución:
Dado: A =
y B =
Asumir,
(AB) T = B T UN T
LHS = RHS
Por lo tanto probado
Pregunta 5: Si A = 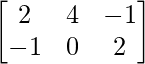 y B =
y B = 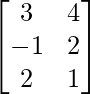 , encuentra (AB)T
, encuentra (AB)T
Solución:
Dado: A =
y B =
Aquí tenemos que encontrar (AB) T
Por eso,
(AB) T =
Pregunta 6:
(i) Para dos arrays A y B, 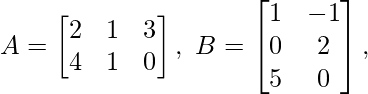 verifique que (AB) T = B T A T
verifique que (AB) T = B T A T
Solución:
Dado,
(AB) T = B T UN T
⇒
⇒
⇒
⇒
⇒ LHS = RHS
Por eso,
(AB) T = B T UN T
(ii) Para las arrays A y B, verifique que (AB) T = B T A T , donde
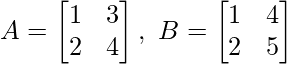
Solución:
Dado,
(AB) T = B T UN T
⇒
⇒
⇒
⇒
⇒ LHS = RH
Asi que,
(AB) T = B T UN T
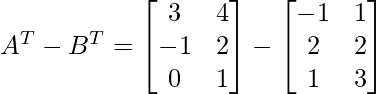
Pregunta 7: Encuentra 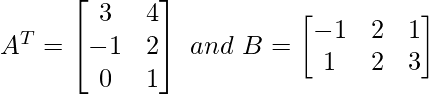 , A T – B T
, A T – B T
Solución:
Dado que
Necesitamos encontrar A T – B T .
Dado que,
Encontremos A T – B T
⇒
⇒
⇒
Pregunta 8: Si 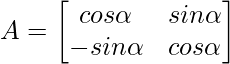 , entonces verifica que A’A = 1
, entonces verifica que A’A = 1
Solución:
⇒
⇒
⇒
Por tanto, hemos comprobado que A’A = I
Pregunta 9: 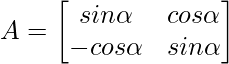 , luego verifica que A’A = I
, luego verifica que A’A = I
Solución:
Por tanto, hemos comprobado que A’A = I
Pregunta 10: Si l i , m i , n i ; i = 1, 2, 3 denote los cosenos directores de tres vectores perpendiculares entre sí en el espacio, demuestre que AA T = I,
Dónde 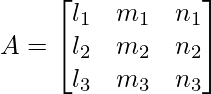
Solución:
Dado,
l i , m i , n i son cosenos directores de tres vectores mutuamente perpendiculares
⇒
Y,
Dado,
= yo
Por eso,
AA T = yo
Publicación traducida automáticamente
Artículo escrito por sudhasinghsudha90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
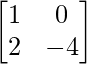

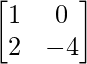

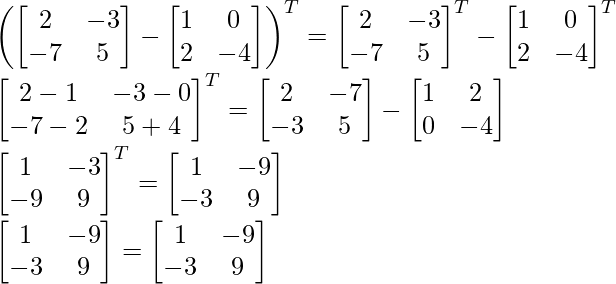
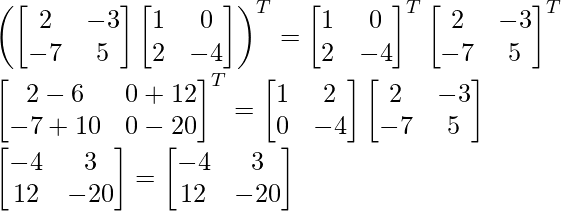
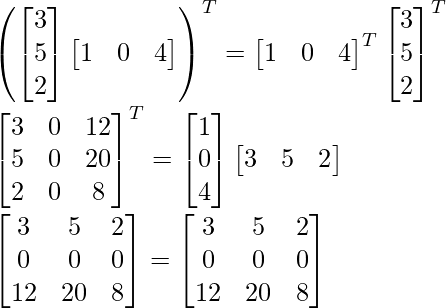
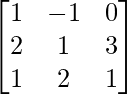


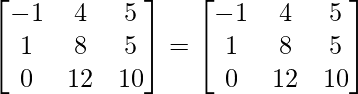

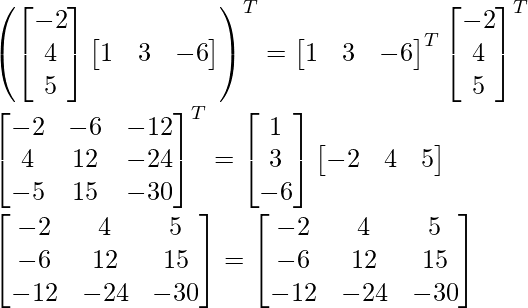
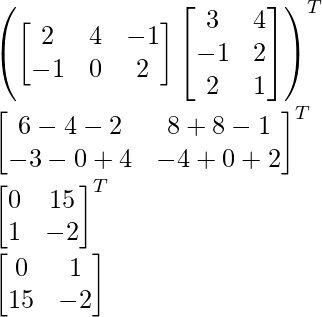
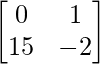
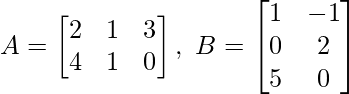
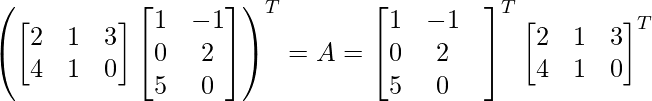

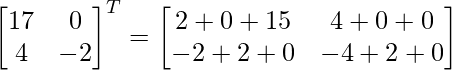
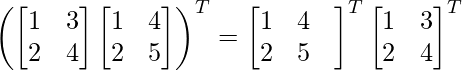
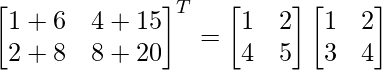
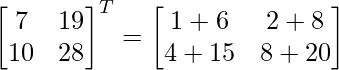
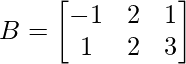
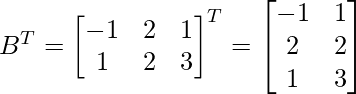

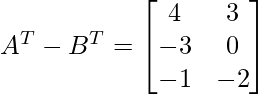

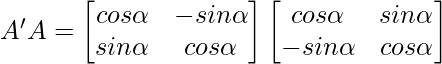


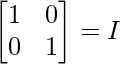
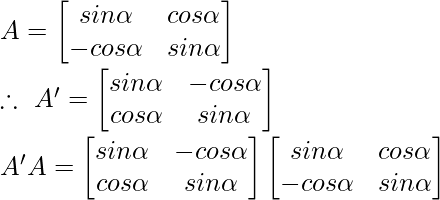
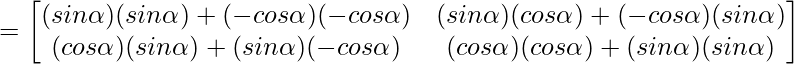
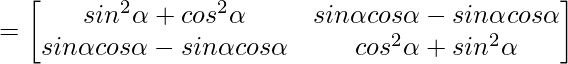
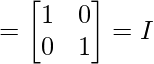
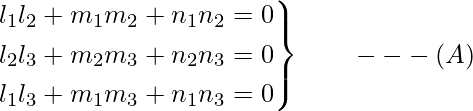
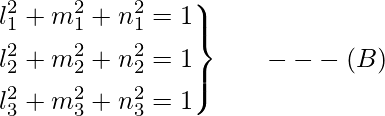
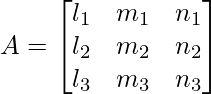
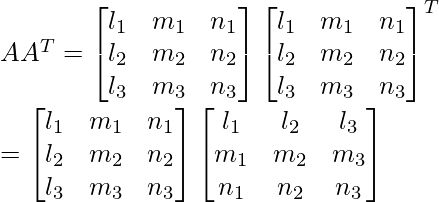

![Rendered by QuickLaTeX.com \begin{bmatrix}1&0&0\\ 0&1&0\\ 0&0&1\end{bmatrix}\ \ \ \ \ \ \ [using\ (A)\ and\ (B)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8ccbd59993353d1fa11bded80491e24e_l3.png)