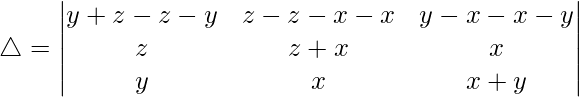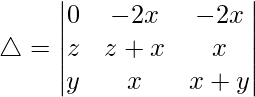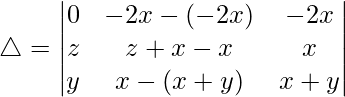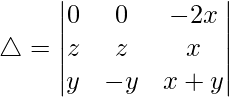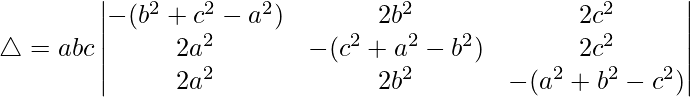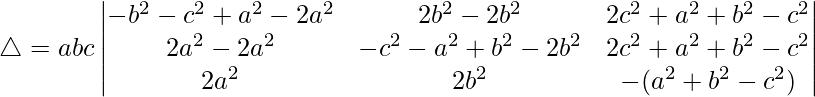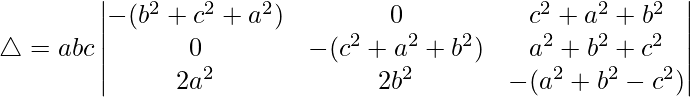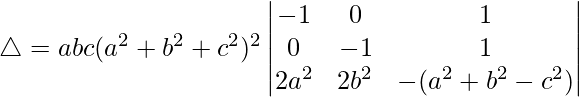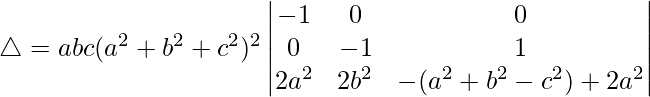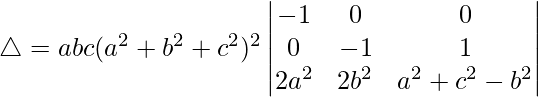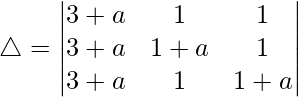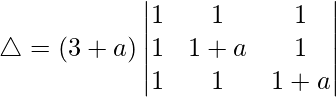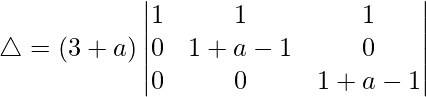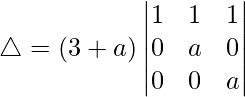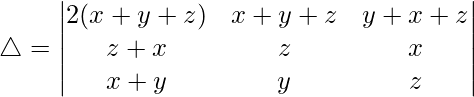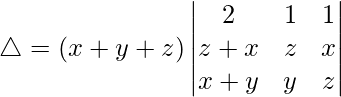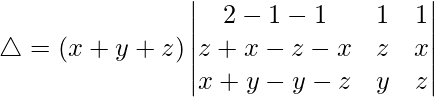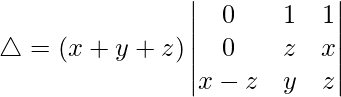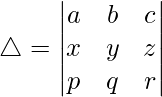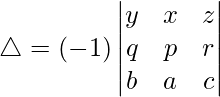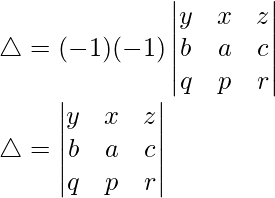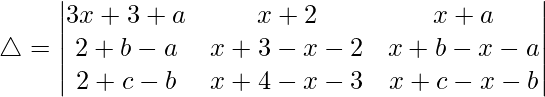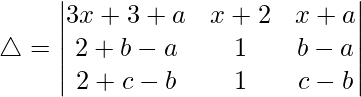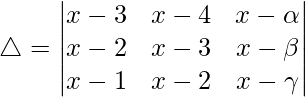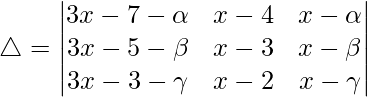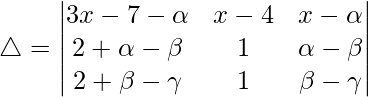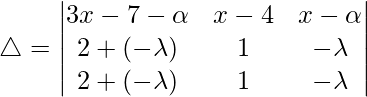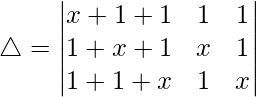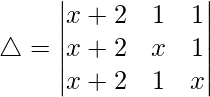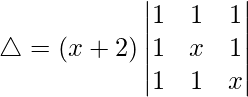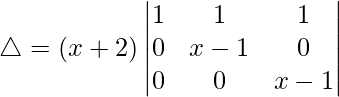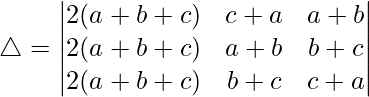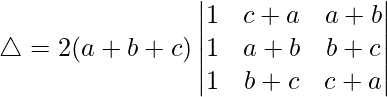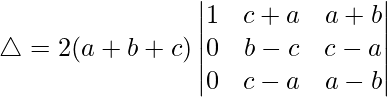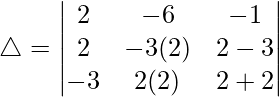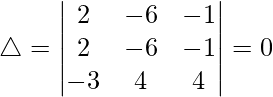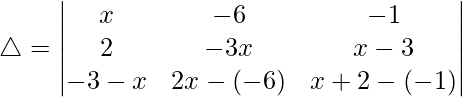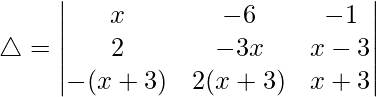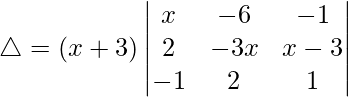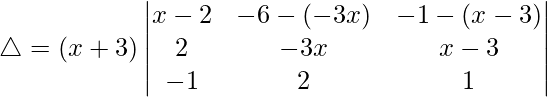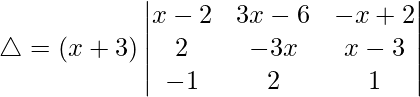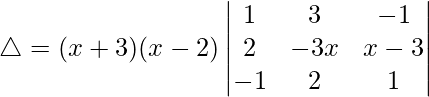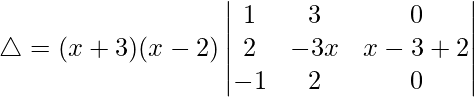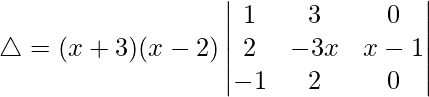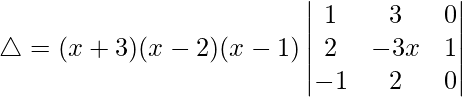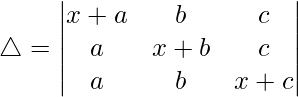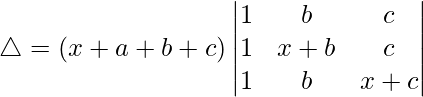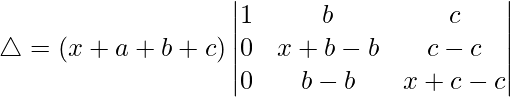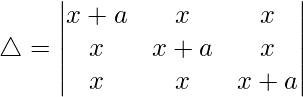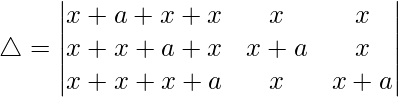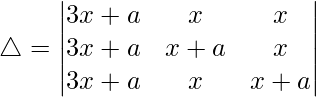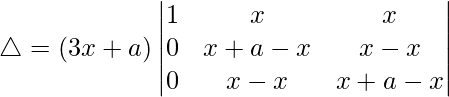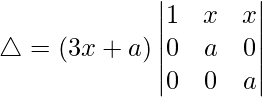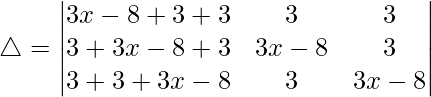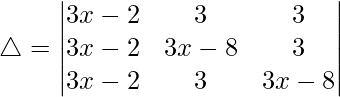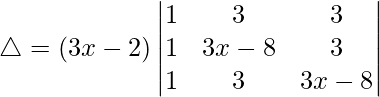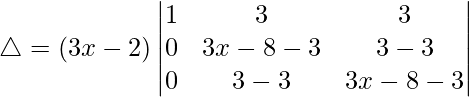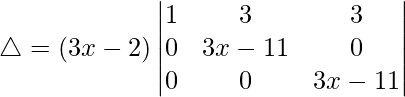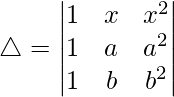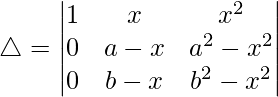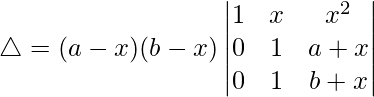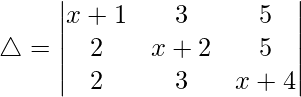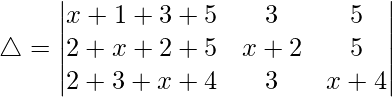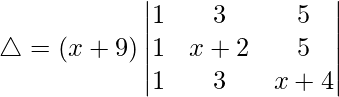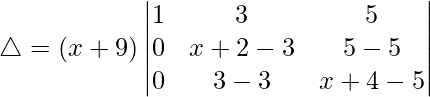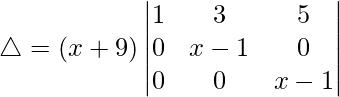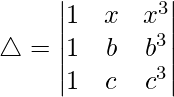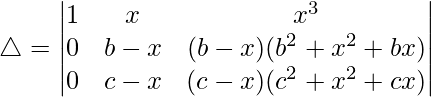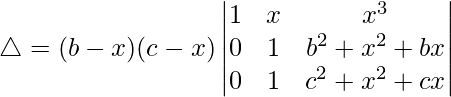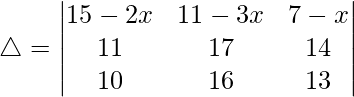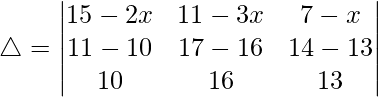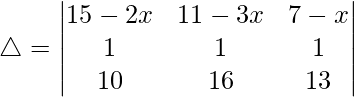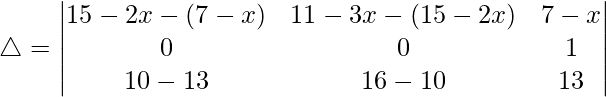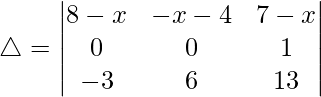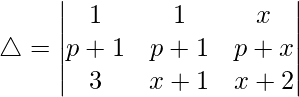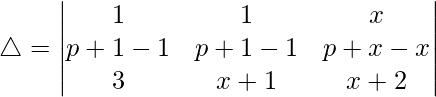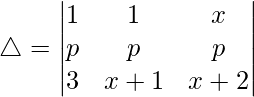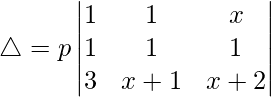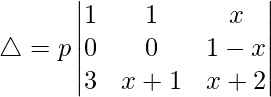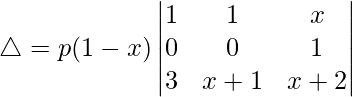Clase 12 Soluciones RD Sharma – Capítulo 6 Determinantes – Ejercicio 6.2

Acreditar las siguientes identidades:

Pregunta 35. 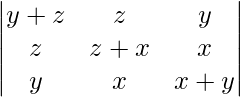$\begin{vmatrix} y+z & z & y \\ z & z+x & x \\ y & x & x+y \end{vmatrix}$ = 4xyz

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} y+z & z & y \\ z & z+x & x \\ y & x & x+y \end{vmatrix}$

R1⇢R1 – R2 – R3

$\triangle = \begin{vmatrix} y+z-z-y & z-z-x-x & y-x-x-y \\ z & z+x & x \\ y & x & x+y \end{vmatrix}$

$\triangle = \begin{vmatrix} 0 & -2x & -2x \\ z & z+x & x \\ y & x & x+y \end{vmatrix}$

C2⇢C2 – C3

$\triangle = \begin{vmatrix} 0 & -2x-(-2x) & -2x \\ z & z+x-x & x \\ y & x-(x+y) & x+y \end{vmatrix}$

$\triangle = \begin{vmatrix} 0 & 0 & -2x \\ z & z & x \\ y & -y & x+y \end{vmatrix}$

△ = [-2x((z)(-y) – (z)(y))]

△ = [-2x(-zy – zy)]

△ = [-2x(-2zy)]

△ = 4xyz

Por lo tanto probado

Pregunta 36. 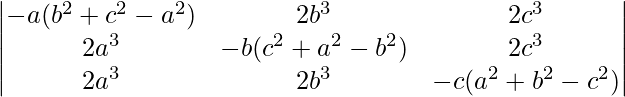$\begin{vmatrix} -a(b^2+c^2-a^2) & 2b^3 & 2c^3 \\ 2a^3 & -b(c^2+a^2-b^2) & 2c^3 \\ 2a^3 & 2b^3 & -c(a^2+b^2-c^2) \end{vmatrix}$ = abc(a ² + b ² + c ² ) ³

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} -a(b^2+c^2-a^2) & 2b^3 & 2c^3 \\ 2a^3 & -b(c^2+a^2-b^2) & 2c^3 \\ 2a^3 & 2b^3 & -c(a^2+b^2-c^2) \end{vmatrix}$

Tomando a, b y c comunes de C1, C2 y C3. Obtenemos

$\triangle = abc\begin{vmatrix} -(b^2+c^2-a^2) & 2b^2 & 2c^2 \\ 2a^2 & -(c^2+a^2-b^2) & 2c^2 \\ 2a^2 & 2b^2 & -(a^2+b^2-c^2) \end{vmatrix}$

R1⇢R1 – R3 y R2⇢R2 – R3

$\triangle = abc\begin{vmatrix} -b^2-c^2+a^2-2a^2 & 2b^2-2b^2 & 2c^2+a^2+b^2-c^2 \\ 2a^2-2a^2 & -c^2-a^2+b^2-2b^2 & 2c^2+a^2+b^2-c^2 \\ 2a^2 & 2b^2 & -(a^2+b^2-c^2) \end{vmatrix}$

$\triangle = abc\begin{vmatrix} -(b^2+c^2+a^2) & 0 & c^2+a^2+b^2 \\ 0 & -(c^2+a^2+b^2) & a^2+b^2+c^2 \\ 2a^2 & 2b^2 & -(a^2+b^2-c^2) \end{vmatrix}$

Tomando (a ² + b ² + c ² ) común de R1 y R2, obtenemos

$\triangle = abc(a^2+b^2+c^2)^2\begin{vmatrix} -1 & 0 & 1 \\ 0 & -1 & 1 \\ 2a^2 & 2b^2 & -(a^2+b^2-c^2) \end{vmatrix}$

C3⇢C3 + C1

$\triangle = abc(a^2+b^2+c^2)^2\begin{vmatrix} -1 & 0 & 0 \\ 0 & -1 & 1 \\ 2a^2 & 2b^2 & -(a^2+b^2-c^2)+2a^2 \end{vmatrix}$

$\triangle = abc(a^2+b^2+c^2)^2\begin{vmatrix} -1 & 0 & 0 \\ 0 & -1 & 1 \\ 2a^2 & 2b^2 & a^2+c^2-b^2 \end{vmatrix}$

△ = abc(a ² + b ² + c ² ) ² [-1((-1)(a ² + c ² – b ² ) – (1)(2b ² ))]

△ = abc(a ² + b ² + c ² ) ² [a ² + c ² – b ² + 2b ² ]

△ = abc(a ² + b ² + c ² ) ² [a ² + c ² + b ² ]

△ = abc(a ² + b ² + c ² ) ³

Por lo tanto probado

Pregunta 37. 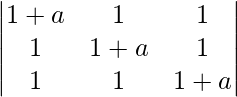$\begin{vmatrix} 1+a & 1 & 1 \\ 1 & 1+a & 1 \\ 1 & 1 & 1+a \end{vmatrix}$ = a ³ + 3a ²

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} 1+a & 1 & 1 \\ 1 & 1+a & 1 \\ 1 & 1 & 1+a \end{vmatrix}$

C1⇢C1 + C2 + C3

$\triangle = \begin{vmatrix} 3+a & 1 & 1 \\ 3+a & 1+a & 1 \\ 3+a & 1 & 1+a \end{vmatrix}$

Tomando (3 + a) común de C1, obtenemos

$\triangle = (3+a)\begin{vmatrix} 1 & 1 & 1 \\ 1 & 1+a & 1 \\ 1 & 1 & 1+a \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R1

$\triangle = (3+a)\begin{vmatrix} 1 & 1 & 1 \\ 0 & 1+a-1 & 0 \\ 0 & 0 & 1+a-1 \end{vmatrix}$

$\triangle = (3+a)\begin{vmatrix} 1 & 1 & 1 \\ 0 & a & 0 \\ 0 & 0 & a \end{vmatrix}$

△ = (3 + a)[1((a)(a) – (0)(0))]

△ = (3 + a)[a ² ]

△ = 3a ² + a ³

Por lo tanto probado

Pregunta 38. 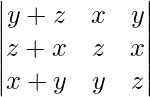$\begin{vmatrix} y+z & x & y \\ z+x & z & x \\ x+y & y & z \end{vmatrix}$ = (x + y + z)(x – z) ²

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} y+z & x & y \\ z+x & z & x \\ x+y & y & z \end{vmatrix}$

R1⇢R1 + R2 + R3

$\triangle = \begin{vmatrix} 2(x+y+z) & x+y+z & y+x+z \\ z+x & z & x \\ x+y & y & z \end{vmatrix}$

Tomando (x + y + z) común de R1, obtenemos

$\triangle = (x+y+z)\begin{vmatrix} 2 & 1 & 1 \\ z+x & z & x \\ x+y & y & z \end{vmatrix}$

C1⇢C1 – C2 – C3

$\triangle = (x+y+z)\begin{vmatrix} 2-1-1 & 1 & 1 \\ z+x-z-x & z & x \\ x+y-y-z & y & z \end{vmatrix}$

$\triangle = (x+y+z)\begin{vmatrix} 0 & 1 & 1 \\ 0 & z & x \\ x-z & y & z \end{vmatrix}$

△ = (x + y + z)[(x – z)(x – z)]

△ = (x + y + z)[(x – z)2]

△ = (x + y + z)(x – z) ²

Por lo tanto probado

Pregunta 39. Sin desarrollar, demuestre que 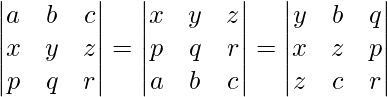$\begin{vmatrix} a & b & c \\ x & y & z \\ p & q & r \end{vmatrix}=\begin{vmatrix} x & y & z \\ p & q & r \\a & b & c \end{vmatrix}=\begin{vmatrix} y & b & q \\ x & z & p \\z & c & r \end{vmatrix}$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} a & b & c \\ x & y & z \\ p & q & r \end{vmatrix}$

R1↔R2

$\triangle = (-1)\begin{vmatrix} x & y & z \\ a & b & c \\ p & q & r \end{vmatrix}$

R2↔R3

$\triangle = (-1)(-1)\begin{vmatrix} x & y & z \\ p & q & r \\ a & b & c \end{vmatrix}\\ \triangle = \begin{vmatrix} x & y & z \\ p & q & r \\ a & b & c \end{vmatrix}$

C1↔C2

$\triangle = (-1)\begin{vmatrix} y & x & z \\ q & p & r \\ b & a & c \end{vmatrix}$

R2↔R3

$\triangle = (-1)(-1)\begin{vmatrix} y & x & z \\ b & a & c \\ q & p & r \end{vmatrix}\\ \triangle = \begin{vmatrix} y & x & z \\ b & a & c \\ q & p & r \end{vmatrix}$

Tomando la transpuesta, tenemos

$\triangle = \begin{vmatrix} y & b & q \\ x & a & p \\ z & c & r \end{vmatrix}$

Por lo tanto probado

$\begin{vmatrix} a & b & c \\ x & y & z \\ p & q & r \end{vmatrix}=\begin{vmatrix} x & y & z \\ p & q & r \\a & b & c \end{vmatrix}=\begin{vmatrix} y & b & q \\ x & z & p \\z & c & r \end{vmatrix}$

Pregunta 40. Muestre que 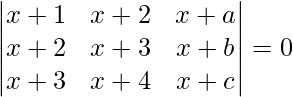$\begin{vmatrix} x+1 & x+2 & x+a \\ x+2 & x+3 & x+b \\ x+3 & x+4 & x+c \end{vmatrix}=0$ donde a, b, c están en AP.

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} x+1 & x+2 & x+a \\ x+2 & x+3 & x+b \\ x+3 & x+4 & x+c \end{vmatrix}$

C1⇢C1 + C2 + C3

$\triangle = \begin{vmatrix} 3x+3+a & x+2 & x+a \\ 3x+5+b & x+3 & x+b \\ 3x+7+c & x+4 & x+c \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R2

$\triangle = \begin{vmatrix} 3x+3+a & x+2 & x+a \\ 2+b-a & x+3-x-2 & x+b-x-a \\ 2+c-b & x+4-x-3 & x+c-x-b \end{vmatrix}$

$\triangle = \begin{vmatrix} 3x+3+a & x+2 & x+a \\ 2+b-a & 1 & b-a \\ 2+c-b & 1 & c-b \end{vmatrix}$

Como a, b y c están en AP

entonces, b – a = c – b = λ

$\triangle = \begin{vmatrix} 3x+3+a & x+2 & x+a \\ 2+\lambda & 1 & \lambda \\ 2+\lambda & 1 & \lambda \end{vmatrix}$

Como, R2 y R3 son idénticos

△ = 0

Por lo tanto probado

Pregunta 41. Muestre que $\begin{vmatrix} x-3 & x-4 & x-\alpha \\ x-2 & x-3 & x-\beta \\ x-1 & x-2 & x-\gamma \end{vmatrix}=0$ donde α, β, γ están en AP.

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} x-3 & x-4 & x-\alpha \\ x-2 & x-3 & x-\beta \\ x-1 & x-2 & x-\gamma \end{vmatrix}$

C1⇢C1 + C2 + C3

$\triangle = \begin{vmatrix} x-3+x-4+x-\alpha & x-4 & x-\alpha \\ x-2+x-3+x-\beta & x-3 & x-\beta \\ x-1+x-2+x-\gamma & x-2 & x-\gamma \end{vmatrix}$

$\triangle = \begin{vmatrix} 3x-7-\alpha & x-4 & x-\alpha \\ 3x-5-\beta & x-3 & x-\beta \\ 3x-3-\gamma & x-2 & x-\gamma \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R2

$\triangle = \begin{vmatrix} 3x-7-\alpha & x-4 & x-\alpha \\ 3x-5-\beta-(3x-7-\alpha) & x-3-(x-4) & x-\beta-(x-\alpha) \\ 3x-3-\gamma-(3x-5-\beta) & x-2-(x-3) & x-\gamma-(x-\beta) \end{vmatrix}$

$\triangle = \begin{vmatrix} 3x-7-\alpha & x-4 & x-\alpha \\ 2+\alpha-\beta & 1 & \alpha-\beta \\ 2+\beta-\gamma & 1 & \beta-\gamma \end{vmatrix}$

Como α, β, γ están en AP

entonces, β – α = γ – β = λ

$\triangle = \begin{vmatrix} 3x-7-\alpha & x-4 & x-\alpha \\ 2+(-\lambda) & 1 & -\lambda \\ 2+(-\lambda) & 1 & -\lambda \end{vmatrix}$

Como, R2 y R3 son idénticos

△ = 0

Por lo tanto probado

Pregunta 42. Evaluar 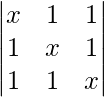$\begin{vmatrix} x & 1 & 1 \\ 1 & x & 1 \\ 1 & 1 & x \end{vmatrix}$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} x & 1 & 1 \\ 1 & x & 1 \\ 1 & 1 & x \end{vmatrix}$

C1⇢C1 + C2 + C3

$\triangle = \begin{vmatrix} x+1+1 & 1 & 1 \\ 1+x+1 & x & 1 \\ 1+1+x & 1 & x \end{vmatrix}$

$\triangle = \begin{vmatrix} x+2 & 1 & 1 \\ x+2 & x & 1 \\ x+2 & 1 & x \end{vmatrix}$

Tomando (x + 2) común de C1. obtenemos

$\triangle = (x+2)\begin{vmatrix} 1 & 1 & 1 \\ 1 & x & 1 \\ 1 & 1 & x \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R2

$\triangle = (x+2)\begin{vmatrix} 1 & 1 & 1 \\ 0 & x-1 & 0 \\ 0 & 0 & x-1 \end{vmatrix}$

△ = (x + 2)[1((x – 1)(x – 1) – (0)(0))]

△ = (x + 2)(x – 1) ²

Por lo tanto probado

Pregunta 43. Si a, b, c son números reales tales que $\begin{vmatrix} b+c & c+a & a+b \\ c+a & a+b & b+c \\ a+b & b+c & c+a \end{vmatrix}=0$ , entonces demuestre que a + b + c = 0 o bien, a = b = c.

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} b+c & c+a & a+b \\ c+a & a+b & b+c \\ a+b & b+c & c+a \end{vmatrix}$

C1⇢C1 + C2 + C3

$\triangle = \begin{vmatrix} 2(a+b+c) & c+a & a+b \\ 2(a+b+c) & a+b & b+c \\ 2(a+b+c) & b+c & c+a \end{vmatrix}$

Tomando 2(a + b + c) comunes de C1. Obtenemos

$\triangle = 2(a+b+c)\begin{vmatrix} 1 & c+a & a+b \\ 1 & a+b & b+c \\ 1 & b+c & c+a \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R2

$\triangle = 2(a+b+c)\begin{vmatrix} 1 & c+a & a+b \\ 0 & a+b-c-a & b+c-a-b \\ 0 & b+c-a-b & c+a-b-c \end{vmatrix}$

$\triangle = 2(a+b+c)\begin{vmatrix} 1 & c+a & a+b \\ 0 & b-c & c-a \\ 0 & c-a & a-b \end{vmatrix}$

△ = 2(a + b + c)[1((b – c)(a – b) – (c – a)(c – a))]

△ = 2(a + b + c)[ba – b ² – ca + cb – (c – a) ² ]

△ = 2(a + b + c)[ba – b ² – ca + cb – (c ² + a ² – 2ac)]

△ = 2(a + b + c)[ba – b ² – ca + cb – c ² – a ² + 2ac]

△ = 2(a + b + c)[ba + bc + ac – b ² – c ² – a ² ]

Como se da que

△ = 0

2 (a + b + c)(ba + bc + ac – b ² – c ² – a ² ) = 0

(a + b + c)(ba + bc + ac – b ² – c ² – a ² ) = 0

Entonces, ya sea (a + b + c) = 0 o (ba + bc + ac – b ² – c ² – a ² ) = 0

Como, ba + bc + ac – b ² – c ² – a ² = 0

Al multiplicarlo por -2, obtenemos

-2ba – 2bc – 2ac + 2b ² + 2c ² + 2a ² = 0

(a – b) ² + (b – c) ² + (c – a) ² = 0

Como, la potencia cuadrada siempre es positiva.

(a – b) ² = (b – c) ² = (c – a) ²

(a – b) = (b – c) = (c – a)

un = segundo = do

Por lo tanto probado

Pregunta 44. Demuestra que x=2 es una raíz de la ecuación 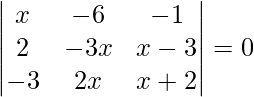$\begin{vmatrix} x & -6 & -1 \\ 2 & -3x & x-3 \\ -3 & 2x & x+2 \end{vmatrix}=0$ y resuélvela completamente.

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} x & -6 & -1 \\ 2 & -3x & x-3 \\ -3 & 2x & x+2 \end{vmatrix}$

Al poner x = 2, obtenemos

$\triangle = \begin{vmatrix} 2 & -6 & -1 \\ 2 & -3(2) & 2-3 \\ -3 & 2(2) & 2+2 \end{vmatrix}$

$\triangle = \begin{vmatrix} 2 & -6 & -1 \\ 2 & -6 & -1 \\ -3 & 4 & 4 \end{vmatrix}=0$

Como, R1 = R2

△ = 0

$\triangle = \begin{vmatrix} x & -6 & -1 \\ 2 & -3x & x-3 \\ -3 & 2x & x+2 \end{vmatrix}$

R3⇢R3 – R1

$\triangle = \begin{vmatrix} x & -6 & -1 \\ 2 & -3x & x-3 \\ -3-x & 2x-(-6) & x+2-(-1) \end{vmatrix}$

$\triangle = \begin{vmatrix} x & -6 & -1 \\ 2 & -3x & x-3 \\ -(x+3) & 2(x+3) & x+3 \end{vmatrix}$

Tomando (x + 3) común de R3, obtenemos

$\triangle = (x+3)\begin{vmatrix} x & -6 & -1 \\ 2 & -3x & x-3 \\ -1 & 2 & 1 \end{vmatrix}$

R1⇢R1 – R2

$\triangle = (x+3)\begin{vmatrix} x-2 & -6-(-3x) & -1-(x-3) \\ 2 & -3x & x-3 \\ -1 & 2 & 1 \end{vmatrix}$

$\triangle = (x+3)\begin{vmatrix} x-2 & 3x-6 & -x+2 \\ 2 & -3x & x-3 \\ -1 & 2 & 1 \end{vmatrix}$

Tomando (x – 2) común de R1. Obtenemos

$\triangle = (x+3)(x-2)\begin{vmatrix} 1 & 3 & -1 \\ 2 & -3x & x-3 \\ -1 & 2 & 1 \end{vmatrix}$

C3⇢C3 + C1

$\triangle = (x+3)(x-2)\begin{vmatrix} 1 & 3 & 0 \\ 2 & -3x & x-3+2 \\ -1 & 2 & 0 \end{vmatrix}$

$\triangle = (x+3)(x-2)\begin{vmatrix} 1 & 3 & 0 \\ 2 & -3x & x-1 \\ -1 & 2 & 0 \end{vmatrix}$

Ahora, tomando (x – 1) común de C3. Obtenemos

$\triangle = (x+3)(x-2)(x-1)\begin{vmatrix} 1 & 3 & 0 \\ 2 & -3x & 1 \\ -1 & 2 & 0 \end{vmatrix}$

△ = (x + 3)(x – 2)(x – 1)[1((1)(2) – (3)(-1))]

△ = (x + 3)(x – 2)(x – 1)[2 + 3]

△ = 5 (x + 3)(x – 2)(x – 1)

△ = 0

5 (x + 3)(x – 2)(x – 1) = 0

x = 2, 1, -3

Pregunta 45. Resuelve las siguientes ecuaciones determinantes:

(i) 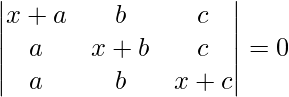$\begin{vmatrix} x+a & b & c \\ a & x+b & c \\ a & b & x+c \end{vmatrix}=0$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} x+a & b & c \\ a & x+b & c \\ a & b & x+c \end{vmatrix}$

C1⇢C1 + C2 + C3

$\triangle = \begin{vmatrix} x+a+b+c & b & c \\ a+x+b+c & x+b & c \\ a+b+x+c & b & x+c \end{vmatrix}$

Ahora, tomando (x + a + b + c) común de C1. Obtenemos

$\triangle = (x+a+b+c)\begin{vmatrix} 1 & b & c \\ 1 & x+b & c \\ 1 & b & x+c \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R1

$\triangle = (x+a+b+c)\begin{vmatrix} 1 & b & c \\ 0 & x+b-b & c-c \\ 0 & b-b & x+c-c \end{vmatrix}$

$\triangle = (x+a+b+c)\begin{vmatrix} 1 & b & c \\ 0 & x & 0 \\ 0 & 0 & x \end{vmatrix}$

△ = (x + a + b + c)[1((x)(x) – (0)(0))]

△ = (x + a + b + c)[x ² ]

Como △ = 0

(x + a + b + c) x ² = 0

x + a + b + c = 0 o x ² = 0

x = -(a + b + c) o x = 0

(ii) 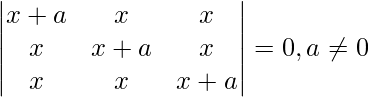$\begin{vmatrix} x+a & x & x \\ x & x+a & x \\ x & x & x+a \end{vmatrix}=0, a \neq0$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} x+a & x & x \\ x & x+a & x \\ x & x & x+a \end{vmatrix}$

C1⇢C1 + C2 + C3

$\triangle = \begin{vmatrix} x+a+x+x & x & x \\ x+x+a+x & x+a & x \\ x+x+x+a & x & x+a \end{vmatrix}$

$\triangle = \begin{vmatrix} 3x+a & x & x \\ 3x+a & x+a & x \\ 3x+a & x & x+a \end{vmatrix}$

Ahora, tomando (3x + a) común de C1. Obtenemos

$\triangle = (3x+a)\begin{vmatrix} 1 & x & x \\ 1 & x+a & x \\ 1 & x & x+a \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R1

$\triangle = (3x+a)\begin{vmatrix} 1 & x & x \\ 0 & x+a-x & x-x \\ 0 & x-x & x+a-x \end{vmatrix}$

$\triangle = (3x+a)\begin{vmatrix} 1 & x & x \\ 0 & a & 0 \\ 0 & 0 & a \end{vmatrix}$

△ = (3x + a)[1((a)(a) – (0)(0))]

△ = (3x + a)[a ² ]

Como △ = 0

(3x + a)[a2] = 0

x = -a/3

(iii) $\begin{vmatrix} 3x-8 & 3 & 3 \\ 3 & 3x-8 & 3 \\ 3 & 3 & 3x-8 \end{vmatrix}=0$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} 3x-8 & 3 & 3 \\ 3 & 3x-8 & 3 \\ 3 & 3 & 3x-8 \end{vmatrix}$

C1⇢C1 + C2 + C3

$\triangle = \begin{vmatrix} 3x-8+3+3 & 3 & 3 \\ 3+3x-8+3 & 3x-8 & 3 \\ 3+3+3x-8 & 3 & 3x-8 \end{vmatrix}$

$\triangle = \begin{vmatrix} 3x-2 & 3 & 3 \\ 3x-2 & 3x-8 & 3 \\ 3x-2 & 3 & 3x-8 \end{vmatrix}$

Ahora, tomando (3x – 2) común de C1. Obtenemos

$\triangle = (3x-2)\begin{vmatrix} 1 & 3 & 3 \\ 1 & 3x-8 & 3 \\ 1 & 3 & 3x-8 \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R1

$\triangle = (3x-2)\begin{vmatrix} 1 & 3 & 3 \\ 0 & 3x-8-3 & 3-3 \\ 0 & 3-3 & 3x-8-3 \end{vmatrix}$

$\triangle = (3x-2)\begin{vmatrix} 1 & 3 & 3 \\ 0 & 3x-11 & 0 \\ 0 & 0 & 3x-11 \end{vmatrix}$

△ = (3x – 2)[1((3x – 11)(3x – 11) – (0)(0))]

△ = (3x – 2)[(3x – 11) ² ]

Como △ = 0

(3x – 2)(3x – 11) ² = 0

3x – 2 = 0 y 3x – 11 = 0

x = 2/3 y x = 11/3

(iv) $\begin{vmatrix} 1 & x & x^2 \\ 1 & a & a^2 \\ 1 & b & b^2 \end{vmatrix}=0, a \neq b$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} 1 & x & x^2 \\ 1 & a & a^2 \\ 1 & b & b^2 \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R1

$\triangle = \begin{vmatrix} 1 & x & x^2 \\ 0 & a-x & a^2-x^2 \\ 0 & b-x & b^2-x^2 \end{vmatrix}$

$\triangle = \begin{vmatrix} 1 & x & x^2 \\ 0 & a-x & (a-x)(a+x) \\ 0 & b-x & (b-x)(b+x) \end{vmatrix}$

Ahora, tomando (a – x) y (b – x) comunes de R2 y R3 respectivamente. Obtenemos

$\triangle = (a-x)(b-x)\begin{vmatrix} 1 & x & x^2 \\ 0 & 1 & a+x \\ 0 & 1 & b+x \end{vmatrix}$

△ = (a – x)(b – x)[1((b + x)(1) – (1)(a + x))]

△ = (a – x)(b – x)[b + x – (a + x)]

△ = (a – x)(b – x)[b + x – a – x]

△ = (a – x)(b – x)[b – a]

Como △ = 0

(a – x)(b – x)(b – a) = 0

a – x = 0 y b – x = 0

x = a y x = b

(v) 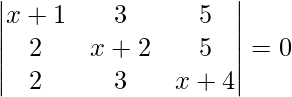$\begin{vmatrix} x+1 & 3 & 5 \\ 2 & x+2 & 5 \\ 2 & 3 & x+4 \end{vmatrix}=0$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} x+1 & 3 & 5 \\ 2 & x+2 & 5 \\ 2 & 3 & x+4 \end{vmatrix}$

C1⇢C1 + C2 + C3

$\triangle = \begin{vmatrix} x+1+3+5 & 3 & 5 \\ 2+x+2+5 & x+2 & 5 \\ 2+3+x+4 & 3 & x+4 \end{vmatrix}$

$\triangle = \begin{vmatrix} x+9 & 3 & 5 \\ x+9 & x+2 & 5 \\ x+9 & 3 & x+4 \end{vmatrix}$

Ahora, tomando (x + 9) común de C1. Obtenemos

$\triangle = (x+9)\begin{vmatrix} 1 & 3 & 5 \\ 1 & x+2 & 5 \\ 1 & 3 & x+4 \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R1

$\triangle = (x+9)\begin{vmatrix} 1 & 3 & 5 \\ 0 & x+2-3 & 5-5 \\ 0 & 3-3 & x+4-5 \end{vmatrix}$

$\triangle = (x+9)\begin{vmatrix} 1 & 3 & 5 \\ 0 & x-1 & 0 \\ 0 & 0 & x-1 \end{vmatrix}$

△ = (x + 9)[1((x – 1)(x – 1) – (0)(0))]

△ = (x + 9)(x – 1) ²

Como △ = 0

(x + 9)(x – 1) ² = 0

x + 9 = 0 o (x – 1) ² = 0

x = -9 o x = 1

(vi) 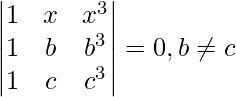$\begin{vmatrix} 1 & x & x^3 \\ 1 & b & b^3 \\ 1 & c & c^3 \end{vmatrix}=0, b \neq c$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} 1 & x & x^3 \\ 1 & b & b^3 \\ 1 & c & c^3 \end{vmatrix}$

R2⇢R2 – R1 y R3⇢R3 – R1

$\triangle = \begin{vmatrix} 1 & x & x^3 \\ 0 & b-x & b^3-x^3 \\ 0 & c-x & c^3-x^3 \end{vmatrix}$

$\triangle = \begin{vmatrix} 1 & x & x^3 \\ 0 & b-x & (b-x)(b^2+x^2+bx) \\ 0 & c-x & (c-x)(c^2+x^2+cx) \end{vmatrix}$

Ahora, tomando (b – x) y (c – x) comunes de R2 y R3 respectivamente. Obtenemos

$\triangle = (b-x)(c-x)\begin{vmatrix} 1 & x & x^3 \\ 0 & 1 & b^2+x^2+bx \\ 0 & 1 & c^2+x^2+cx \end{vmatrix}$

△ = (b – x)(c – x)[1((c ² + x ² + cx)(1) – (b ² + x ² + bx)(1))]

△ = (b – x)(c – x)[(c ² + x ² + cx) – (b ² + x ² + bx)]

△ = (b – x)(c – x)

△ = (b – x)(c – x)

△ = (b – x)(c – x)[(c – b)(c + b) + x(c – b)]

△ = (b – x)(c – x)(c – b)

Como △ = 0

(b – x)(c – x)(c – b) = 0

b – x = 0 o c – x = 0 o c – b = 0 o c + b + x = 0

x = b o x = c o c = b o x = -(c + b)

(vii) 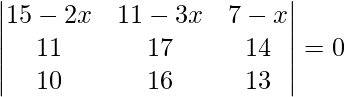$\begin{vmatrix} 15-2x & 11-3x & 7-x \\ 11 & 17 & 14 \\ 10 & 16 & 13 \end{vmatrix}=0$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} 15-2x & 11-3x & 7-x \\ 11 & 17 & 14 \\ 10 & 16 & 13 \end{vmatrix}$

R2⇢R2 – R3

$\triangle = \begin{vmatrix} 15-2x & 11-3x & 7-x \\ 11-10 & 17-16 & 14-13 \\ 10 & 16 & 13 \end{vmatrix}$

$\triangle = \begin{vmatrix} 15-2x & 11-3x & 7-x \\ 1 & 1 & 1 \\ 10 & 16 & 13 \end{vmatrix}$

R2⇢R2 – R1 y R1⇢R1 – R3

$\triangle = \begin{vmatrix} 15-2x-(7-x) & 11-3x-(15-2x) & 7-x \\ 0 & 0 & 1 \\ 10-13 & 16-10 & 13 \end{vmatrix}$

$\triangle = \begin{vmatrix} 8-x & -x-4 & 7-x \\ 0 & 0 & 1 \\ -3 & 6 & 13 \end{vmatrix}$

△ = -1[(8 – x)(6) – (-x – 4)(-3)]

△ = -1[(8 – x)(6) – (x + 4)(3)]

△ = [(x + 4)(3) – (8 – x)(6)]

△ = [3x + 12 – (48 – 6x)]

△ = [9x – 36]

Como △ = 0

9x – 36 = 0

x = 4

(viii) $\begin{vmatrix} 1 & 1 & x \\ p+1 & p+1 & p+x \\ 3 & x+1 & x+2 \end{vmatrix}=0$

Solución:

Teniendo en cuenta el determinante, tenemos

$\triangle = \begin{vmatrix} 1 & 1 & x \\ p+1 & p+1 & p+x \\ 3 & x+1 & x+2 \end{vmatrix}$

R2⇢R2 – R1

$\triangle = \begin{vmatrix} 1 & 1 & x \\ p+1-1 & p+1-1 & p+x-x \\ 3 & x+1 & x+2 \end{vmatrix}$

$\triangle = \begin{vmatrix} 1 & 1 & x \\ p & p & p \\ 3 & x+1 & x+2 \end{vmatrix}$

Ahora, tomando p común de R2. Obtenemos

$\triangle = p\begin{vmatrix} 1 & 1 & x \\ 1 & 1 & 1 \\ 3 & x+1 & x+2 \end{vmatrix}$

R2⇢R2 – R1

$\triangle = p\begin{vmatrix} 1 & 1 & x \\ 0 & 0 & 1-x \\ 3 & x+1 & x+2 \end{vmatrix}$

Ahora, tomando 1 – x común de R2. Obtenemos

$\triangle = p(1-x)\begin{vmatrix} 1 & 1 & x \\ 0 & 0 & 1 \\ 3 & x+1 & x+2 \end{vmatrix}$

△ = pag(1 – x)[-1((x + 1)(1) – (3)(1))]

△ = pag(x – 1)[x + 1 – 3]

△ = pag(x – 1)[x – 2]

Como △ = 0

p(x-1)(x-2) = 0

x – 1 = 0 o x – 2 = 0

x = 1 o x = 2

Publicación traducida automáticamente

Artículo escrito por adi1212 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 6 Determinantes – Ejercicio 6.2 | conjunto 3

Acreditar las siguientes identidades:

Pregunta 35. $\begin{vmatrix} y+z & z & y \\ z & z+x & x \\ y & x & x+y \end{vmatrix}$ = 4xyz

Pregunta 36. $\begin{vmatrix} -a(b^2+c^2-a^2) & 2b^3 & 2c^3 \\ 2a^3 & -b(c^2+a^2-b^2) & 2c^3 \\ 2a^3 & 2b^3 & -c(a^2+b^2-c^2) \end{vmatrix}$ = abc(a ² + b ² + c ² ) ³

Pregunta 37. $\begin{vmatrix} 1+a & 1 & 1 \\ 1 & 1+a & 1 \\ 1 & 1 & 1+a \end{vmatrix}$ = a ³ + 3a ²

Pregunta 38. $\begin{vmatrix} y+z & x & y \\ z+x & z & x \\ x+y & y & z \end{vmatrix}$ = (x + y + z)(x – z) ²

Pregunta 39. Sin desarrollar, demuestre que $\begin{vmatrix} a & b & c \\ x & y & z \\ p & q & r \end{vmatrix}=\begin{vmatrix} x & y & z \\ p & q & r \\a & b & c \end{vmatrix}=\begin{vmatrix} y & b & q \\ x & z & p \\z & c & r \end{vmatrix}$

Pregunta 40. Muestre que $\begin{vmatrix} x+1 & x+2 & x+a \\ x+2 & x+3 & x+b \\ x+3 & x+4 & x+c \end{vmatrix}=0$ donde a, b, c están en AP.

Pregunta 41. Muestre que $\begin{vmatrix} x-3 & x-4 & x-\alpha \\ x-2 & x-3 & x-\beta \\ x-1 & x-2 & x-\gamma \end{vmatrix}=0$ donde α, β, γ están en AP.

Pregunta 42. Evaluar $\begin{vmatrix} x & 1 & 1 \\ 1 & x & 1 \\ 1 & 1 & x \end{vmatrix}$

Pregunta 43. Si a, b, c son números reales tales que $\begin{vmatrix} b+c & c+a & a+b \\ c+a & a+b & b+c \\ a+b & b+c & c+a \end{vmatrix}=0$ , entonces demuestre que a + b + c = 0 o bien, a = b = c.

Pregunta 44. Demuestra que x=2 es una raíz de la ecuación $\begin{vmatrix} x & -6 & -1 \\ 2 & -3x & x-3 \\ -3 & 2x & x+2 \end{vmatrix}=0$ y resuélvela completamente.

Pregunta 45. Resuelve las siguientes ecuaciones determinantes:

(i) $\begin{vmatrix} x+a & b & c \\ a & x+b & c \\ a & b & x+c \end{vmatrix}=0$

(ii) $\begin{vmatrix} x+a & x & x \\ x & x+a & x \\ x & x & x+a \end{vmatrix}=0, a \neq0$

(iii) $\begin{vmatrix} 3x-8 & 3 & 3 \\ 3 & 3x-8 & 3 \\ 3 & 3 & 3x-8 \end{vmatrix}=0$

(iv) $\begin{vmatrix} 1 & x & x^2 \\ 1 & a & a^2 \\ 1 & b & b^2 \end{vmatrix}=0, a \neq b$

(v) $\begin{vmatrix} x+1 & 3 & 5 \\ 2 & x+2 & 5 \\ 2 & 3 & x+4 \end{vmatrix}=0$

(vi) $\begin{vmatrix} 1 & x & x^3 \\ 1 & b & b^3 \\ 1 & c & c^3 \end{vmatrix}=0, b \neq c$

(vii) $\begin{vmatrix} 15-2x & 11-3x & 7-x \\ 11 & 17 & 14 \\ 10 & 16 & 13 \end{vmatrix}=0$

(viii) $\begin{vmatrix} 1 & 1 & x \\ p+1 & p+1 & p+x \\ 3 & x+1 & x+2 \end{vmatrix}=0$

Deja una respuesta Cancelar la respuesta

Acreditar las siguientes identidades:

Pregunta 35. = 4xyz

Pregunta 36. = abc(a 2 + b 2 + c 2 ) 3

Pregunta 37. = a 3 + 3a 2

Pregunta 38. = (x + y + z)(x – z) 2

Pregunta 39. Sin desarrollar, demuestre que

Pregunta 40. Muestre que donde a, b, c están en AP.

Pregunta 41. Muestre que donde α, β, γ están en AP.

Pregunta 42. Evaluar

Pregunta 43. Si a, b, c son números reales tales que , entonces demuestre que a + b + c = 0 o bien, a = b = c.

Pregunta 44. Demuestra que x=2 es una raíz de la ecuación y resuélvela completamente.

Pregunta 45. Resuelve las siguientes ecuaciones determinantes:

(i)

(ii)

(iii)

(iv)

(v)

(vi)

(vii)

(viii)

Deja una respuesta Cancelar la respuesta

Pregunta 35. $\begin{vmatrix} y+z & z & y \\ z & z+x & x \\ y & x & x+y \end{vmatrix}$ = 4xyz

Pregunta 36. $\begin{vmatrix} -a(b^2+c^2-a^2) & 2b^3 & 2c^3 \\ 2a^3 & -b(c^2+a^2-b^2) & 2c^3 \\ 2a^3 & 2b^3 & -c(a^2+b^2-c^2) \end{vmatrix}$ = abc(a ² + b ² + c ² ) ³

Pregunta 37. $\begin{vmatrix} 1+a & 1 & 1 \\ 1 & 1+a & 1 \\ 1 & 1 & 1+a \end{vmatrix}$ = a ³ + 3a ²

Pregunta 38. $\begin{vmatrix} y+z & x & y \\ z+x & z & x \\ x+y & y & z \end{vmatrix}$ = (x + y + z)(x – z) ²

Pregunta 39. Sin desarrollar, demuestre que $\begin{vmatrix} a & b & c \\ x & y & z \\ p & q & r \end{vmatrix}=\begin{vmatrix} x & y & z \\ p & q & r \\a & b & c \end{vmatrix}=\begin{vmatrix} y & b & q \\ x & z & p \\z & c & r \end{vmatrix}$

Pregunta 40. Muestre que $\begin{vmatrix} x+1 & x+2 & x+a \\ x+2 & x+3 & x+b \\ x+3 & x+4 & x+c \end{vmatrix}=0$ donde a, b, c están en AP.

Pregunta 41. Muestre que $\begin{vmatrix} x-3 & x-4 & x-\alpha \\ x-2 & x-3 & x-\beta \\ x-1 & x-2 & x-\gamma \end{vmatrix}=0$ donde α, β, γ están en AP.

Pregunta 42. Evaluar $\begin{vmatrix} x & 1 & 1 \\ 1 & x & 1 \\ 1 & 1 & x \end{vmatrix}$

Pregunta 43. Si a, b, c son números reales tales que $\begin{vmatrix} b+c & c+a & a+b \\ c+a & a+b & b+c \\ a+b & b+c & c+a \end{vmatrix}=0$ , entonces demuestre que a + b + c = 0 o bien, a = b = c.

Pregunta 44. Demuestra que x=2 es una raíz de la ecuación $\begin{vmatrix} x & -6 & -1 \\ 2 & -3x & x-3 \\ -3 & 2x & x+2 \end{vmatrix}=0$ y resuélvela completamente.

(i) $\begin{vmatrix} x+a & b & c \\ a & x+b & c \\ a & b & x+c \end{vmatrix}=0$

(ii) $\begin{vmatrix} x+a & x & x \\ x & x+a & x \\ x & x & x+a \end{vmatrix}=0, a \neq0$

(iii) $\begin{vmatrix} 3x-8 & 3 & 3 \\ 3 & 3x-8 & 3 \\ 3 & 3 & 3x-8 \end{vmatrix}=0$

(iv) $\begin{vmatrix} 1 & x & x^2 \\ 1 & a & a^2 \\ 1 & b & b^2 \end{vmatrix}=0, a \neq b$

(v) $\begin{vmatrix} x+1 & 3 & 5 \\ 2 & x+2 & 5 \\ 2 & 3 & x+4 \end{vmatrix}=0$

(vi) $\begin{vmatrix} 1 & x & x^3 \\ 1 & b & b^3 \\ 1 & c & c^3 \end{vmatrix}=0, b \neq c$

(vii) $\begin{vmatrix} 15-2x & 11-3x & 7-x \\ 11 & 17 & 14 \\ 10 & 16 & 13 \end{vmatrix}=0$

(viii) $\begin{vmatrix} 1 & 1 & x \\ p+1 & p+1 & p+x \\ 3 & x+1 & x+2 \end{vmatrix}=0$