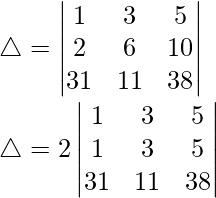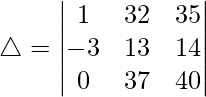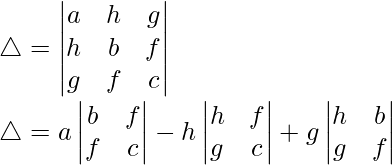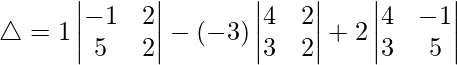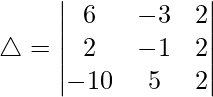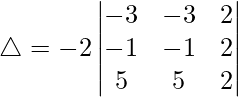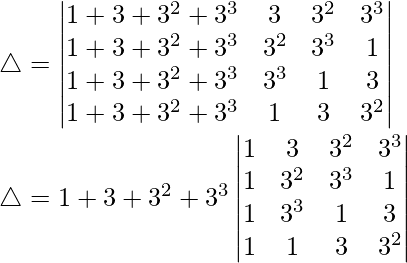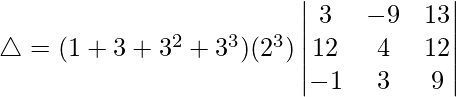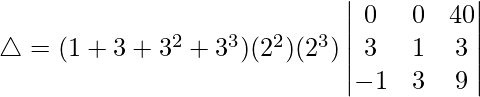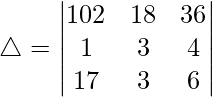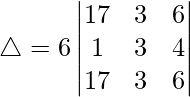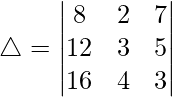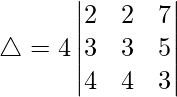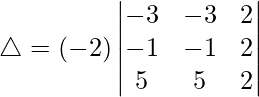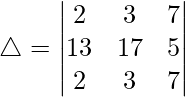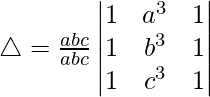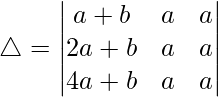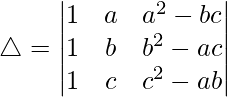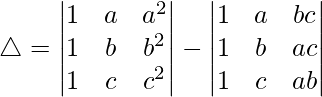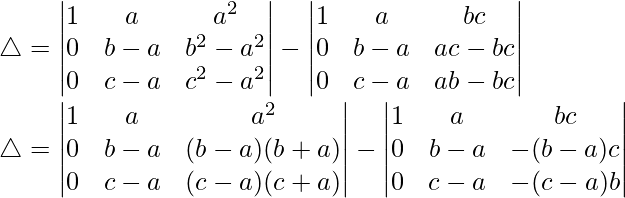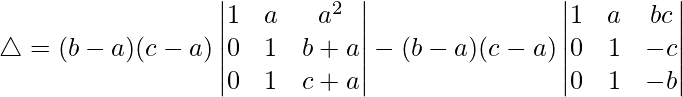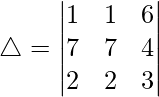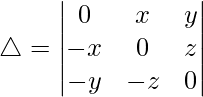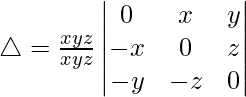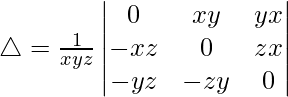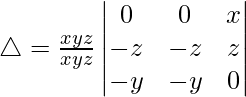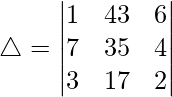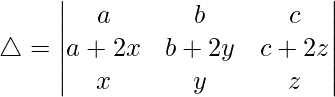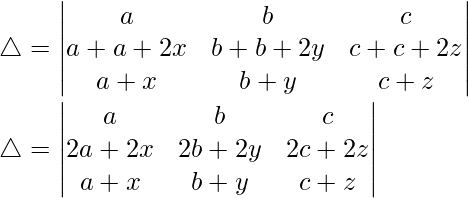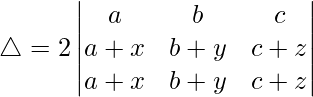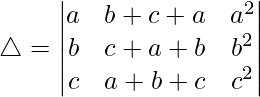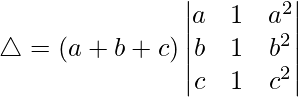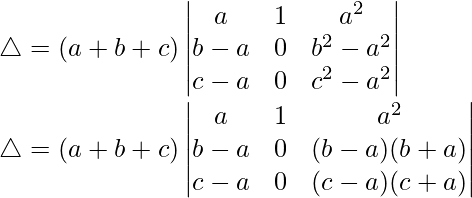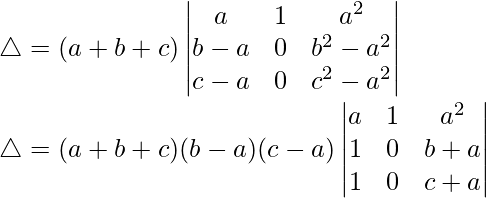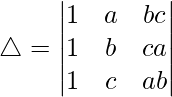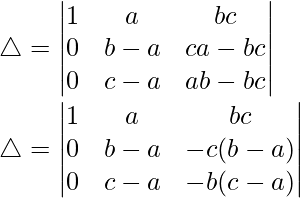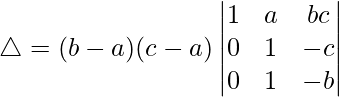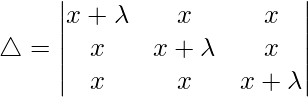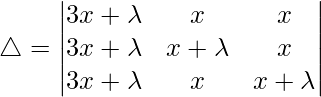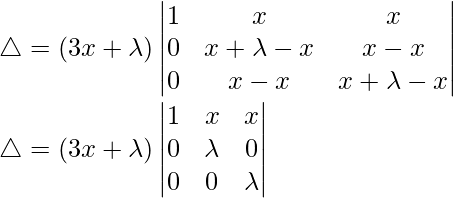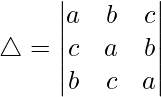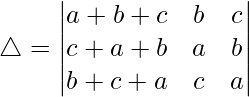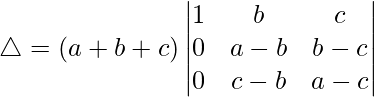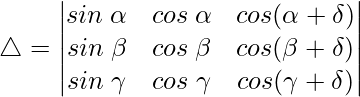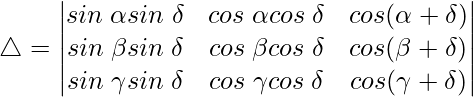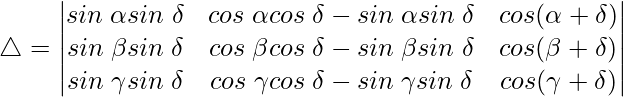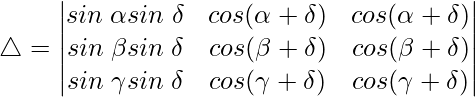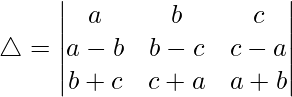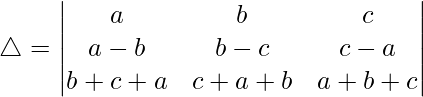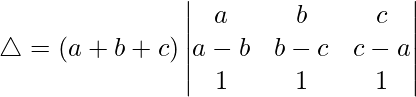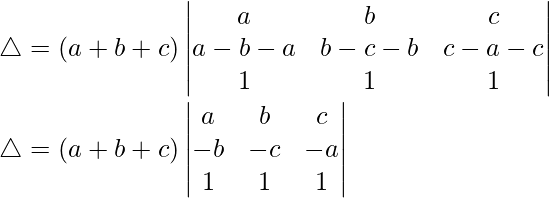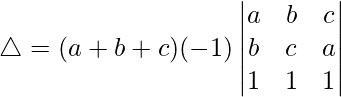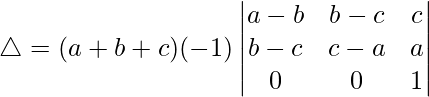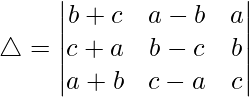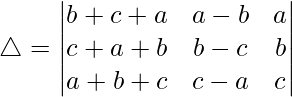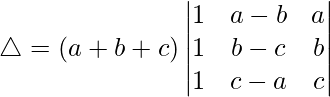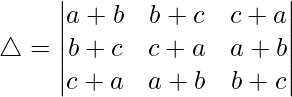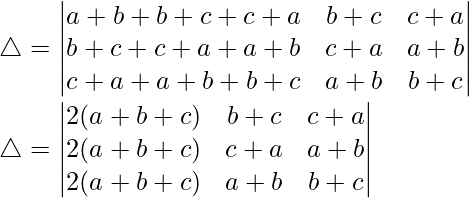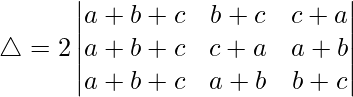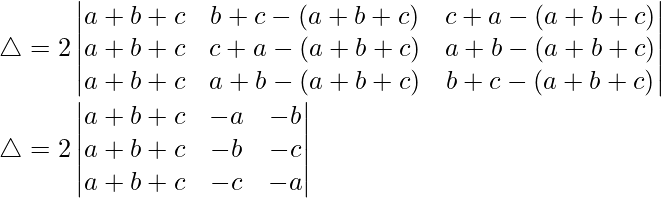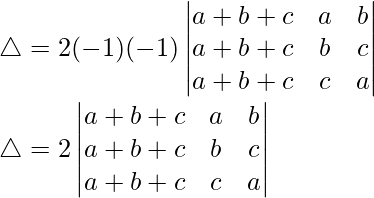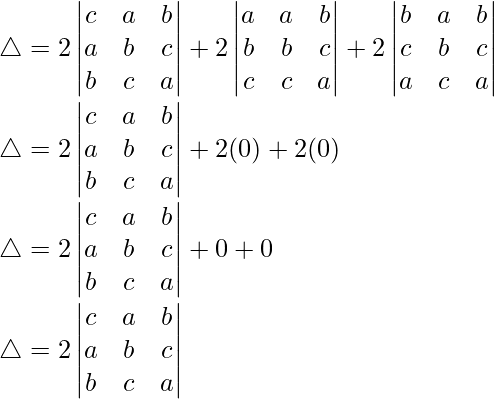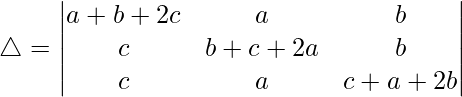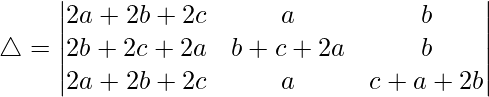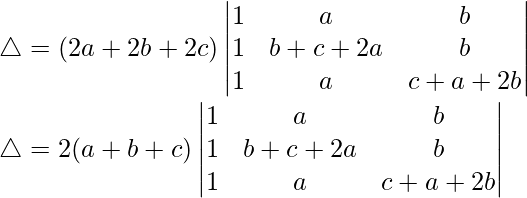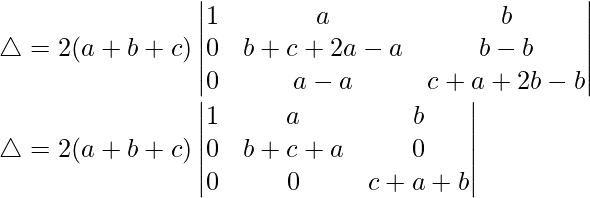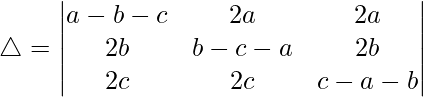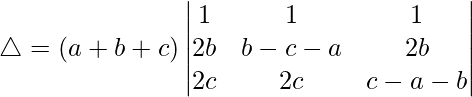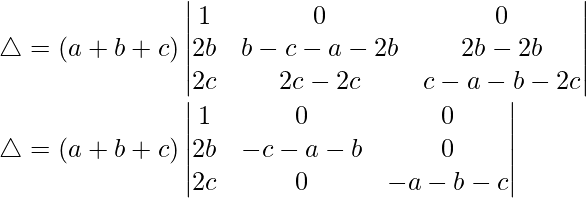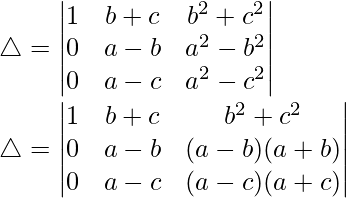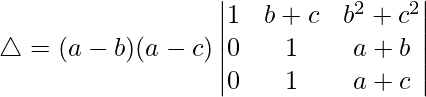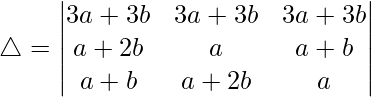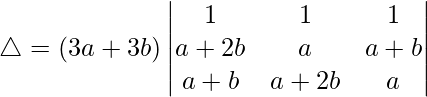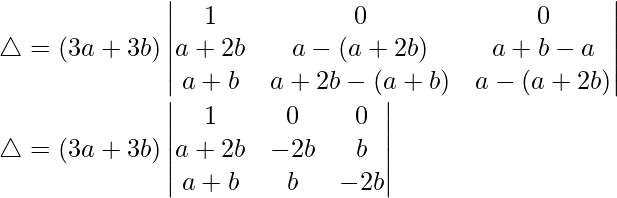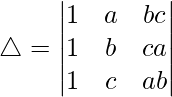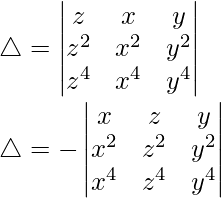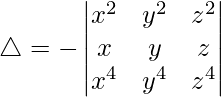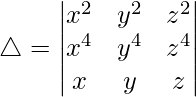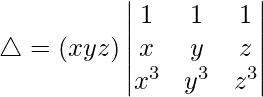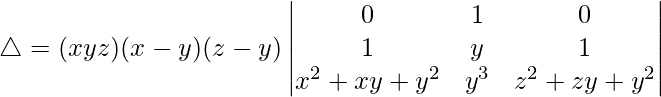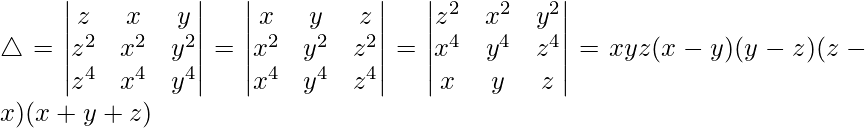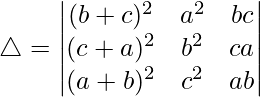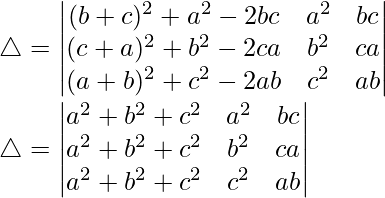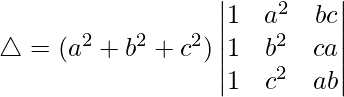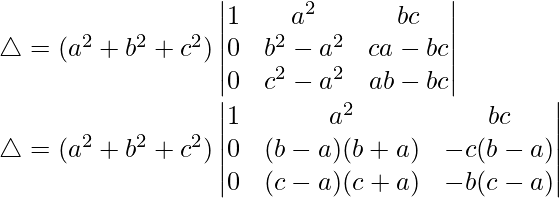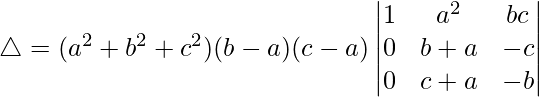Pregunta 1. Evalúa el siguiente determinante:
(i) 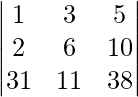
Solución:
Teniendo en cuenta el determinante, tenemos
Como R1 y R2 son idénticos
Por lo tanto, △ = 0
(ii) 
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 – 3C3
R3⇢R3 + R2 y R1⇢R1 + R2
R2⇢R2 + 3R1
△ = 1(109 × 40 – 119 × 37)
Por lo tanto, △ = -43
(iii) 
Solución:
Teniendo en cuenta el determinante, tenemos
△ = a(bc – f 2 ) – h(hc – fg) + g(hf – gb)
△ = abc – af 2 – h 2 c + fgh + fgh – gramo 2 segundo
Por lo tanto, △ = abc + 2fgh – af 2 – ch 2 – bg 2
(iv) 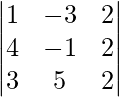
Solución:
Teniendo en cuenta el determinante, tenemos
△ = 1(-2 – 10) + 3(8 – 6) + 2(20 + 3)
△ = 1(-12) + 3(2) + 2(23)
△ = -12 + 6 + 46
Por lo tanto, △ = 40
(v) 
Solución:
Teniendo en cuenta el determinante, tenemos
△ = 1(225-256) + 4(100-144) + 9(64-81)
△ = 1(-31) – 4(-44) + 9(-17)
△ = -31 + 176 – 153
Por lo tanto, △ = -8
(vi) 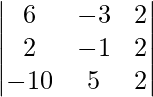
Solución:
Teniendo en cuenta el determinante, tenemos
Tomando -2 común de C1, C2 y C3
Como C1 y C2 son idénticos
Por lo tanto, △ = 0
(vii) 
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 + C3
C2⇢C2 – C1
C3⇢C3 – C1
C4⇢C4 – C1
Tomando 2, -2 y -2 comunes de C1, C2 y C3
Tomando 4 comunes de R2 y R1⇢R1+3R3
△ = (1 + 3 + 32 + 33)(4)(8)[40(9 – (-1))]
△ = (40)(4)(8)[40(9 + 1)]
△ = 40 × 4 × 8 × 40 × 10
Por lo tanto, △ = 512000
(viii) 
Solución:
Teniendo en cuenta el determinante, tenemos
Tomando 6 comunes de R1, obtenemos
Como R1 y R3 son idénticos
Por lo tanto, △ = 0
Pregunta 2. Sin desarrollar, muestra que los valores de cada uno de los siguientes determinantes son cero:
(i) 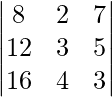
Solución:
Teniendo en cuenta el determinante, tenemos
Tomando 4 comunes de C1, obtenemos
Como C1 y C2 son idénticos
Por lo tanto, △ = 0
(ii) 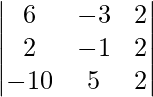
Solución:
Teniendo en cuenta el determinante, tenemos
Tomando -2 común de C1, obtenemos
Como C1 y C2 son idénticos
Por lo tanto, △ = 0
(iii) 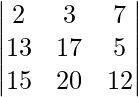
Solución:
Teniendo en cuenta el determinante, tenemos
R3⇢R3 – R2
Como R1 y R3 son idénticos
Por lo tanto, △ = 0
(iv) 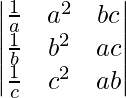
Solución:
Teniendo en cuenta el determinante, tenemos
Multiplicando y dividiendo △ por abc, obtenemos
Multiplicando R1, R2 y R3 por a, b y c respectivamente
Tomando abc común de C3, obtenemos
Como C2 y C3 son idénticos
Por lo tanto, △ = 0
(v) 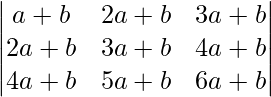
Solución:
Teniendo en cuenta el determinante, tenemos
C3⇢C3 – C2 y C2⇢C2 – C1
Como C2 y C3 son idénticos
Por lo tanto, △ = 0
(vi) 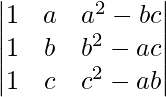
Solución:
Teniendo en cuenta el determinante, tenemos
Dividiendo el determinante, tenemos
R2⇢R2-R1 y R3⇢R3-R1
Tomando (ba) y (ca) comunes de R2 y R3, tenemos
△ = (b – a)(c – a)(c + a – (b + a)) – (b – a)(c – a)(-b – (-c))
△ = (b – a)(c – a)(c + a – b – a) – (b – a)(c – a)(-b + c)
△ = (b – a)(c – a)(c – b) – (b – a)(c – a)(c – b)
Por lo tanto, △ = 0
(vii) 
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 – 8C3
Como C1 y C2 son idénticos
Por lo tanto, △ = 0
(viii) 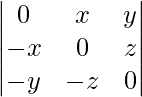
Solución:
Teniendo en cuenta el determinante, tenemos
Multiplicando y dividiendo por xyz, tenemos
Multiplicando C1, C2 y C3 por z, y y x respectivamente
Tomando y, x y z comunes en R1, R2 y R3 respectivamente
C2⇢C2 – C3
Como C1 y C2 son idénticos
Por lo tanto, △ = 0
(ix) 
Solución:
Teniendo en cuenta el determinante, tenemos
C2⇢C2 – 7C3
Como C1 y C2 son idénticos
Por lo tanto, △ = 0
(X) 
Solución:
Teniendo en cuenta el determinante, tenemos
C3⇢C3 – C2 y C4⇢C4 – C1
Tomando 3 comunes de C3, obtenemos
Como C3 y C4 son idénticos
Por lo tanto, △ = 0
(xi) 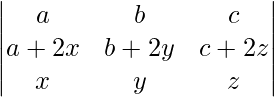
Solución:
Teniendo en cuenta el determinante, tenemos
R3⇢R3 + R1 y R2⇢R2 + R1
Tomando 2 comunes de R2, obtenemos
Como R2 y R3 son idénticos
Por lo tanto, △ = 0
Pregunta 3. 
Solución:
Teniendo en cuenta el determinante, tenemos
C2⇢C2+C1
Tomando (a+b+c) común de C2, obtenemos
R3⇢R3-R1 y R2⇢R2-R1
Tomando (b – a) y (c – a) de R2 y R3, tenemos
△ = (a + b + c)(b – a)(c – a)[1(b + a – (c + a))]
△ = (a + b + c)(b – a)(c – a)(b + a – c – a)
Por lo tanto, △ = (a + b + c)(b – a)(c – a)(b – c)
Pregunta 4. 
Solución:
Teniendo en cuenta el determinante, tenemos
R3⇢R3-R1 y R2⇢R2-R1
Tomando (ba) y (ca) de R2 y R3, tenemos
△ = (b – a)(c – a)[1((1)(-b) – (1)(-c))]
△ = (b – a)(c – a)[-b – (-c)]
△ = (b – a)(c – a)[-b + c]
Por lo tanto, △ = (a – b)(b – c)(c – a)
Pregunta 5. 
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1+C2+C3
Tomando (3x+λ) común de C1, obtenemos
R3⇢R3-R1 y R2⇢R2-R1
△ = (3x + λ)[λ(λ(1) – 0)]
△ = (3x + λ)[λ(λ)]
Por lo tanto, △ = λ 2 (3x + λ)
Pregunta 6. 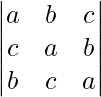
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 + C3
Tomando (a + b + c) común de C1, obtenemos
R3⇢R3 – R1 y R2⇢R2 – R1
△ = (a + b + c)[1((a – b)(a – c) – (c – b)(b – c))]
△ = (a + b + c)[(a 2 – ac – ab + bc) – (cb – c 2 – b 2 + bc)]
△ = (a + b + c)[a 2 – ac – ab + bc + c 2 + b 2 – 2bc]
Por lo tanto, △ = (a + b + c)[a 2 + b 2 + c 2 – ac – ab – bc]
Pregunta 7. 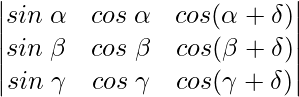
Solución:
Teniendo en cuenta el determinante, tenemos
C2⇢C2 – C1
Usando la identidad trigonométrica,
cos a cos b – sen a sen b = cos (a + b)
Como C2 y C3 son idénticos
Por lo tanto, △ = 0
Acreditar las siguientes identidades:
Pregunta 8. 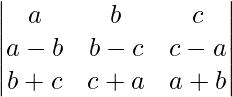 = a 3 + b 2 + c 3 – 3abc
= a 3 + b 2 + c 3 – 3abc
Solución:
Teniendo en cuenta el determinante, tenemos
R3⇢R3 + R1 y R2⇢R2 + R1
Tomando (a + b + c) común de R3, obtenemos
R2⇢R2 – R1
Tomando (-1) común de R2, obtenemos
C1⇢C1 – C2 y C2⇢C2 – C3
△ = (-1)(a + b + c)[1((a – b)(c – a) – (b – c)(b – c))]
△ = (-1)(a + b + c)[(a – b)(c – a) – (b – c) 2 ]
△ = (-1)(a + b + c)[(ac – a 2 – bc + ab) – (b 2 – 2cb + c 2 )]
△ = (-1)(a + b + c)(ac – a 2 – bc + ab – b 2 + 2cb – c 2 )
△ = (a + b + c)(-ac + a 2 – bc – ab + b 2 + c 2 )
△ = (a + b + c)(a 2 + b 2 + c 2 – ac – ab – cb)
△ = un 3 + segundo 3 + do 3 – 3abc
Por lo tanto probado
Pregunta 9. 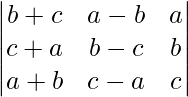 = 3abc – a 3 – b 2 – c 3
= 3abc – a 3 – b 2 – c 3
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C3
Tomando (a + b + c) común de C1, obtenemos
△ = (a + b + c)[1((b – c)c – b(c – a)) – 1((a – b)c – a(c – a)) + 1(b(a – b) – a(b – c))]
△ = (a + b + c)[(b – c)c – b(c – a) – (a – b)c + a(c – a) + b(a – b) – a(b – c )]
△ = (a + b + c)[(bc – c 2 -bc + ab) – (ac – bc) + ac – a 2 + ab – b 2 – (ab – ac)]
△ = (a + b + c)[bc – c 2 – bc + ab – ac + bc + ac – a 2 + ab – b 2 – ab + ac]
△ = (a + b + c)[bc – c 2 + ab + ac – a 2 – b 2 ]
△ = (a + b + c)[bc + ab + ac – a 2 – b 2 – c 2 ]
△ = 3abc – a 3 – b 3 – c 3
Por lo tanto probado
Pregunta 10. 
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 + C3
Tomando 2 comunes de C1, obtenemos
C2⇢C2 – C1 y C3⇢C3 – C1
Tomando (-1) y (-1) comunes de C2 y C3,
Al dividir el determinante, obtenemos
Por lo tanto probado
Pregunta 11. 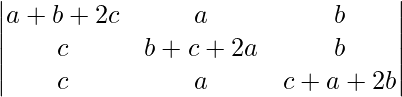 = 2(a + b + c) 3
= 2(a + b + c) 3
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 + C3
Tomando (2a + 2b + 2c) común de C1, obtenemos
R2⇢R2 – R1 y R3⇢R3 – R1
△ = 2(a + b + c)[1((a + b + b)(a + b + c) – 0)]
△ = 2(a + b + c)[(a + b + b) 2 ]
△ = 2(a + b + c) 3
Por lo tanto probado
Pregunta 12. 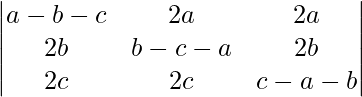 = (a + b + c) 3
= (a + b + c) 3
Solución:
Teniendo en cuenta el determinante, tenemos
R1⇢R1 + R2 + R3
Tomando (a + b + c) común de R1, obtenemos
C2⇢C2 – C1 y C3⇢C3 – C1
△ = (a + b + c)[1((-b – c – a)(-b – c – a) – 0)]
△ = (a + b + c)[(b + c + a)(b + c + a)]
△ = (a + b + c)[(b + c + a) 2 ]
△ = (a + b + c) 3
Por lo tanto probado
Pregunta 13. 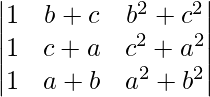 = (a – b)(b – c)(c – a)
= (a – b)(b – c)(c – a)
Solución:
Teniendo en cuenta el determinante, tenemos
R2⇢R2 – R1 y R3⇢R3 – R1
Tomando (a – b) y (a – c) comunes de R2 y R3 respectivamente, obtenemos
△ = (a – b)(a – c)[1(1(a + c) – 1(a + b))]
△ = (a – b)(a – c)[(a + c) – (a + b)]
△ = (a – b)(a – c)[a + c – a – b]
△ = (a – b)(a – c)
△ = (a – b)(a – c)(c – b)
△ = (a – b)(b – c)(c – a)
Por lo tanto probado
Pregunta 14. 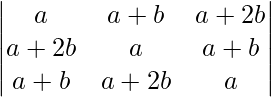 = 9(a + b)b 2
= 9(a + b)b 2
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 + C3
Tomando (3a + 3b) común de R1, obtenemos
C2⇢C2 – C1 y C3⇢C3 – C2
△ = 3(a + b)[1((-2b)(-2b) – b(b))]
△ = 3(a + b)[4b 2 – b 2 ]
△ = 3(a + b)[3b 2 ]
△ = 9(a + b)b 2
Por lo tanto probado
Pregunta 15. 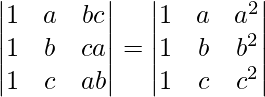
Solución:
Teniendo en cuenta el determinante, tenemos
R1⇢aR1, R2⇢bR2 y R3⇢cR3
Tomando (abc) común de C3, obtenemos
Por lo tanto probado
Pregunta 16. 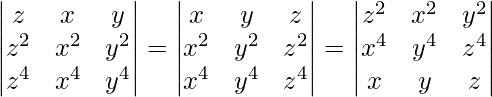 = xyz(x – y)(y – z)(z – x)(x + y + z)
= xyz(x – y)(y – z)(z – x)(x + y + z)
Solución:
Teniendo en cuenta el determinante, tenemos
C1↔C2 y luego
C2↔C3
R1↔R2
R2↔R3
Tomando,
Tomando x, y y z comunes de C1, C2 y C3 respectivamente
C1⇢C1 – C2 y C3⇢C3 – C2
Tomando (x – y) y (z – y) comunes de C1 y C3 respectivamente, obtenemos
△ = (xyz)(x – y)(z – y)[1(1(z 2 + zy + y 2 ) – 1(x 2 + xy + y 2 ))]
△ = (xyz)(x – y)(z – y)[z 2 + zy + y 2 – (x 2 + xy + y 2 )]
△ = (xyz)(x – y)(z – y)[z 2 + zy + y 2 – x 2 – xy – y 2 ]
△ = (xyz)(x – y)(z – y)[z 2 + zy – x 2 – xy]
△ = (xyz)(x – y)(z – y)[z 2 – x 2 + zy – xy]
△ = (xyz)(x – y)(z – y)[(z – x)(z + x) + y(z – x)]
△ = (xyz)(x – y)(z – y)(z – x)[z + x + y]
△ = (xyz)(x – y)(z – y)(z – x)(x + y + z)
Por lo tanto probado
Pregunta 17. 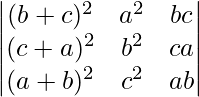 = (a – b)(b – c)(c – a)(a + b + c)(a 2 + b 2 + c 2 )
= (a – b)(b – c)(c – a)(a + b + c)(a 2 + b 2 + c 2 )
Solución:
Teniendo en cuenta el determinante, tenemos
C1⇢C1 + C2 – 2C3
Tomando (a 2 + b 2 + c 2 ) común de C1, obtenemos
C2⇢C2-C1 y C3⇢C3-C1
Tomando (b – a) y (c – a) comunes de R2 y R3, obtenemos
△ = (a 2 + b 2 + c 2 )(b – a)(c – a)[1((b + a)(-b) – (c + a)(-c))]
△ = (a 2 + b 2 + c 2 )(b – a)(c – a)[(b + a)(-b) + (c + a)c]
△ = (a 2 + b 2 + c 2 )(b – a)(c – a)[(-b 2 – ab) + (c 2 + ac)]
△ = (a 2 + b 2 + c 2 )(b – a)(c – a)
△ = (a 2 + b 2 + c 2 )(b – a)(c – a)[(c – b)(c + b) + a(c – b)]
△ = (a 2 + b 2 + c 2 )(b – a)(c – a)(c – b)
△ = (a 2 + b 2 + c 2 )(a + b + c)(a – b)(b – c)(c – a)
Por lo tanto probado