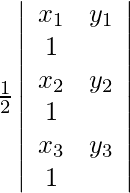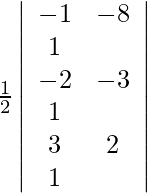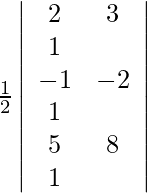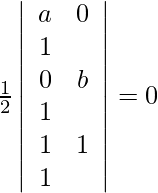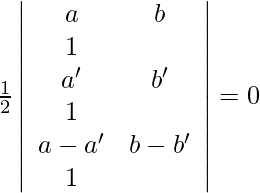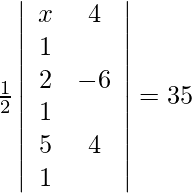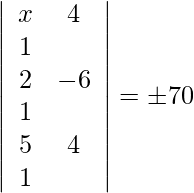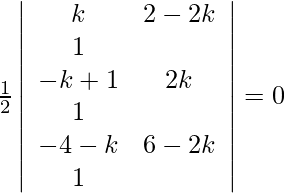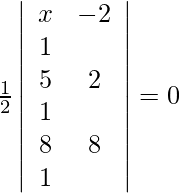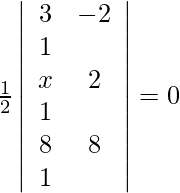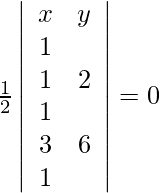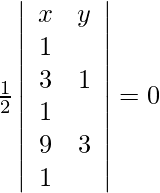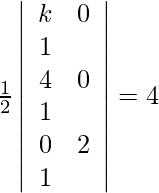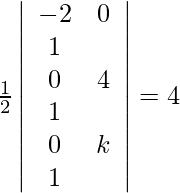Clase 12 RD Sharma Solutions – Capítulo 6 Determinantes – Ejercicio 6.3

Pregunta 1. Encuentra el área del triángulo con vértices en los puntos:

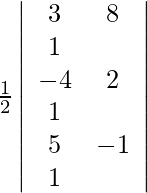
(i) (3, 8), (−4, 2) y (5, −1)

Solución:

Dados (3, 8), (−4, 2) y (5, −1) son los vértices del triángulo.

Sabemos que, si los vértices de un triángulo son (x ₁ , y ₁ ), (x ₂ , y ₂ ) y (x ₃ , y ₃ ), entonces el área del triángulo está dada por,

un = $\frac{1}{2} \left| \begin{array}{cc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{array} \right|$

= $\frac{1}{2} \left| \begin{array}{cc} 3 & 8 & 1 \\ -4 & 2 & 1 \\ 5 & -1 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[3(2+1)-8(-4-5)+1(4-10)]$

= $\frac{1}{2}[9+72-6]$

= $\frac{75}{2}$

Por lo tanto, el área del triángulo es $\frac{75}{2}$ unidades cuadradas.

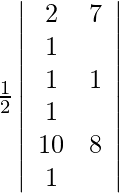
(ii) (2, 7), (1, 1) y (10, 8)

Solución:

Dados (2, 7), (1, 1) y (10, 8) son los vértices del triángulo.

El área del triángulo está dada por,

un = $\frac{1}{2} \left| \begin{array}{cc} 2 & 7 & 1 \\ 1 & 1 & 1 \\ 10 & 8 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[2(1-8)-7(1-10)+1(8-10)]$

= $\frac{1}{2}[-14+63-2]$

= $\frac{47}{2}$

Por lo tanto, el área del triángulo es $\frac{47}{2}$ unidades cuadradas.

(iii) (−1, −8), (−2, −3) y (3, 2)

Solución:

Dado (−1, −8), (−2, −3) y (3, 2) son los vértices del triángulo.

El área del triángulo está dada por,

un = $\frac{1}{2} \left| \begin{array}{cc} -1 & -8 & 1 \\ -2 & -3 & 1 \\ 3 & 2 & 1 \\ \end{array} \right|$

= $\frac{1}{2}|-1(-3-2)+8(-2-3)+1(-4+9)|$

= $\frac{1}{2}|5-40+5|$

= $\frac{30}{2}$

= 15

Por lo tanto, el área del triángulo es de 15 unidades cuadradas.

(iv) (0, 0), (6, 0), (4, 3)

Solución:

Dados (0, 0), (6, 0), (4, 3) son los vértices del triángulo.

El área del triángulo está dada por,

un = $\frac{1}{2} \left| \begin{array}{cc} 0 & 0 & 1 \\ 6 & 0 & 1 \\ 4 & 3 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[0-0+1(18-0)]$

= $\frac{18}{2}$

= 9

Por lo tanto, el área del triángulo es de 9 unidades cuadradas.

Pregunta 2. Utilizando los determinantes, demuestre que los siguientes puntos son colineales:

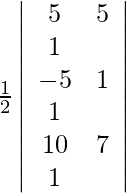
(i) (5, 5), (−5, 1) y (10, 7)

Solución:

Los puntos dados son (5, 5), (−5, 1) y (10, 7).

Para que estos puntos sean colineales, el área del triángulo que forman debe ser cero. Entonces, obtenemos,

un = $\frac{1}{2} \left| \begin{array}{cc} 5 & 5 & 1 \\ -5 & 1 & 1 \\ 10 & 7 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[5(1-7)-5(-5-10)+1(-35-10)]$

= $\frac{1}{2}[-30+75-45]$

= 0

Como el área del triángulo es 0, los puntos son colineales.

Por lo tanto probado.

(ii) (1, −1), (2, 1) y (4, 5)

Solución:

Los puntos dados son (1, −1), (2, 1) y (10, 8).

Para que estos puntos sean colineales, el área del triángulo que forman debe ser cero. Entonces, obtenemos,

un = $\frac{1}{2} \left| \begin{array}{cc} 1 & -1 & 1 \\ 2 & 1 & 1 \\ 4 & 5 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[1(1-5)+1(2-4)+1(10-4)]$

= $\frac{1}{2}[-4-2+6]$

= 0

Como el área del triángulo es 0, los puntos son colineales.

Por lo tanto probado.

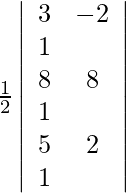
(iii) (3, −2), (8, 8) y (5, 2)

Solución:

Los puntos dados son (3, −2), (8, 8) y (5, 2).

Para que estos puntos sean colineales, el área del triángulo que forman debe ser cero. Entonces, obtenemos,

un = $\frac{1}{2} \left| \begin{array}{cc} 3 & -2 & 1 \\ 8 & 8 & 1 \\ 5 & 2 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[3(8-2)+2(8-5)+1(16-40)]$

= $\frac{1}{2}[18+6-24]$

= 0

Como el área del triángulo es 0, los puntos son colineales.

Por lo tanto probado.

(iv) (2, 3), (−1, −2) y (5, 8)

Solución:

Los puntos dados son (2, 3), (−1, −2) y (5, 8).

Para que estos puntos sean colineales, el área del triángulo que forman debe ser cero. Entonces, obtenemos,

un = $\frac{1}{2} \left| \begin{array}{cc} 2 & 3 & 1 \\ -1 & -2 & 1 \\ 5 & 8 & 1 \\ \end{array} \right|$

= $\frac{1}{2}[2(-2-8)-3(-1-5)+1(-8+10)]$

= $\frac{1}{2}[-20+18+2]$

= 0

Como el área del triángulo es 0, los puntos son colineales.

Por lo tanto probado.

Pregunta 3. Si los puntos (a, 0), (0, b) y (1, 1) son colineales, prueba que a + b = ab.

Solución:

Dados los puntos (a, 0), (0, b) y (1, 1) son colineales.

Para que estos puntos sean colineales, el área del triángulo que forman debe ser cero. Entonces, obtenemos,

=> $\frac{1}{2} \left| \begin{array}{cc} a & 0 & 1 \\ 0 & b & 1 \\ 1 & 1 & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[a(b-1)-0+1(0-b)]=0$

=> ab − a − b = 0

=> a + b = ab

Por lo tanto probado.

Pregunta 4. Utilizando los determinantes, demuestre que los puntos (a, b), (a’, b’) y (a – a’, b – b) son colineales si a b’ = a’ b.

Solución:

Los puntos dados son (a, b), (a’, b’) y (a – a’, b – b) y a b’ = a’ b.

Para que estos puntos sean colineales, el área del triángulo que forman debe ser cero. Entonces, obtenemos,

=> $\frac{1}{2} \left| \begin{array}{cc} a & b & 1 \\ a' & b' & 1 \\ a - a' & b - b' & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[a(b'-b+b')-b(a'-a+a')+1(a'b-a'b'-ab'+a'b')]=0$

=> $\frac{1}{2}[ab'-ab+ab'-a'b+ab-a'b+a'b-ab')]=0$

=> un segundo’ − un’ segundo = 0

=> un segundo’ = un’ segundo

Por lo tanto probado.

Pregunta 5. Encuentra el valor de λ para que los puntos (1, −5), (−4, 5) y (λ, 7) sean colineales.

Solución:

Los puntos dados son (1, −5), (−4, 5) y (λ, 7).

Para que estos puntos sean colineales, el área del triángulo que forman debe ser cero. Entonces, obtenemos,

=> $\frac{1}{2} \left| \begin{array}{cc} 1 & -5 & 1 \\ -4 & 5 & 1 \\ λ & 7 & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[1(5-7)+5(-4-λ)+1(-28-5λ)]=0$

=> −2 − 20 − 5λ − 28 − 5λ = 0

=> 10λ = 50

=> λ = 5

Por lo tanto, el valor de λ es 5.

Pregunta 6. Encuentra el valor de x si el área de ∆ es de 35 cm cuadrados con vértices (x, 4), (2, −6) y (5, 4).

Solución:

Los puntos dados son (x, 4), (2, −6) y (5, 4).

Sabemos que, si los vértices de un triángulo son (x ₁ , y ₁ ), (x ₂ , y ₂ ) y (x ₃ , y ₃ ), entonces el área del triángulo está dada por,

un = $\frac{1}{2} \left| \begin{array}{cc} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \\ \end{array} \right|$

=> $\frac{1}{2} \left| \begin{array}{cc} x & 4 & 1 \\ 2 & -6 & 1 \\ 5 & 4 & 1 \\ \end{array} \right| = 35$

=> $\left| \begin{array}{cc} x & 4 & 1 \\ 2 & -6 & 1 \\ 5 & 4 & 1 \\ \end{array} \right| = \pm70$

=> − 10x + 12 + 38 = ±70

=> – 10x + 50 = ±70

Tomando signo positivo, obtenemos

=> – 10x + 50 = 70

=> 10x = – 20

=> x = – 2

Tomando signo negativo, obtenemos

=> – 10x + 50 = – 70

=> 10x = 120

=> x = 12

Por lo tanto, el valor de x es 12 o –2.

Pregunta 7. Usando determinantes, encuentra el área del triángulo cuyos vértices son (1, 4), (2, 3), (–5, –3). ¿Los puntos dados son colineales?

Solución:

Los puntos dados son (1, 4), (2, 3), (–5, –3).

Entonces, área = $\frac{1}{2} \left| \begin{array}{cc} 1 & 4 & 1 \\ 2 & 3 & 1 \\ -5 & -3 & 1 \\ \end{array} \right|$

= $\frac{1}{2}|1(3+3)-4(2+5)+1(-6+15)|$

= $\frac{1}{2}|6-28+9|$

= $\frac{13}{2}$

Como el área del triángulo formado por estos tres puntos no es cero, los puntos no son colineales.

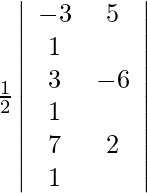
Pregunta 8. Usando determinantes, encuentra el área del triángulo con vértices (–3, 5), (3, –6), (7, 2).

Los puntos dados son (–3, 5), (3, –6), (7, 2).

Entonces, área = $\frac{1}{2} \left| \begin{array}{cc} -3 & 5 & 1 \\ 3 & -6 & 1 \\ 7 & 2 & 1 \\ \end{array} \right|$

= $\frac{1}{2}|-3(-6-2)-5(3-7)+1(6+42)|$

= $\frac{1}{2}|24+20+48|$

= $\frac{92}{2}$

= 46

Por lo tanto, el área del triángulo es de 46 unidades cuadradas.

Pregunta 9. Usando determinantes, encuentre el valor de k para que los puntos (k, 2–2k), (–k+1, 2k), (–4–k, 6–2k) puedan ser colineales.

Solución:

Los puntos dados son (k, 2–2k), (–k+1, 2k), (–4–k, 6–2k). Como los puntos son colineales, el área debe ser 0.

=> $\frac{1}{2} \left| \begin{array}{cc} k & 2-2k & 1 \\ -k+1 & 2k & 1 \\ -4-k & 6-2k & 1 \\ \end{array} \right|=0$

=> k(2k – 6 + 2k) – (2–2k) (–k + 1 + 4 + k) + [(1–k) (6–2k) – 2k (–4–k)] = 0

=> 8k ² + 4k – 4 = 0

=> 8k ² + 8k – 4k – 4 = 0

=> 8k (k+1) – 4 (k+1) = 0

=> 8k = 4 o k = –1

=> k = 1/2 o k = –1

Por lo tanto, el valor de k es 1/2 o –1.

Pregunta 10. Si los puntos (x, –2), (5, 2), (8, 8) son colineales, encuentra x usando determinantes.

Solución:

Los puntos dados son (x, –2), (5, 2), (8, 8). Como los puntos son colineales, el área debe ser 0.

=> $\frac{1}{2} \left| \begin{array}{cc} x & -2 & 1 \\ 5 & 2 & 1 \\ 8 & 8 & 1 \\ \end{array} \right|=0$

=> x(2 – 8) + 2(5 – 8) + 1(40–16) = 0

=> –6x – 6 + 24 = 0

=> 6x = 18

=> x = 3

Por lo tanto, el valor de x es 3.

Pregunta 11. Si los puntos (3, –2), (x, 2), (8, 8) son colineales, encuentra x usando determinantes.

Solución:

Los puntos dados son (3, –2), (x, 2), (8, 8). Como los puntos son colineales, el área debe ser 0.

=> $\frac{1}{2} \left| \begin{array}{cc} 3 & -2 & 1 \\ x & 2 & 1 \\ 8 & 8 & 1 \\ \end{array} \right|=0$

=> 3(2 – 8) + 2(x – 8) + 1(8x–16) = 0

=> –18 + 2x – 16 + 8x – 16 = 0

=> 10x = 50

=> x = 5

Por lo tanto, el valor de x es 5.

Pregunta 12. Usando determinantes, encuentre la ecuación de

(i) la línea que une los puntos (1, 2) y (3, 6).

Solución:

Sean (x, y), (1, 2), (3, 6) los puntos de la recta. Como estos puntos son colineales, obtenemos,

=> $\frac{1}{2} \left| \begin{array}{cc} x & y & 1 \\ 1 & 2 & 1 \\ 3 & 6 & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[x(2-6)-y(1-3)+1(6-6)]=0$

=> −4x + 2y = 0

=> 2x − y = 0

Por lo tanto, la ecuación requerida es 2x − y = 0.

(ii) la línea que une los puntos (3, 1) y (9, 3).

Solución:

Sean (x, y), (3, 1), (9, 3) los puntos de la recta. Como estos puntos son colineales, obtenemos,

=> $\frac{1}{2} \left| \begin{array}{cc} x & y & 1 \\ 3 & 1 & 1 \\ 9 & 3 & 1 \\ \end{array} \right|=0$

=> $\frac{1}{2}[x(1-3)-y(3-6)+1(9-9)]=0$

=> −2x + 6y = 0

=> x − 3y = 0

Por lo tanto, la ecuación requerida es x − 3y = 0.

Pregunta 13. Encuentra los valores de k

(i) si el área del triángulo cuyos vértices son (k, 0) (4, 0) (0, 2) es 4 unidades cuadradas.

Solución:

Los puntos dados son (k, 0) (4, 0) (0, 2). De acuerdo con la pregunta, tenemos,

=> $\frac{1}{2} \left| \begin{array}{cc} k & 0 & 1 \\ 4 & 0 & 1 \\ 0 & 2 & 1 \\ \end{array} \right|=4$

=> |k(0−2) − 0 + 1(8−0)| = 8

=> −2k + 8 = ±8

=> −2k + 8 = 8 o −2k + 8 = −8

=> k = 0 o k = 8

Por lo tanto, el valor de k es 0 u 8.

(ii) si el área del triángulo cuyos vértices son (−2, 0) (0, 4) (0, k) es 4 unidades cuadradas.

Solución:

Los puntos dados son (−2, 0) (0, 4) (0, k). De acuerdo con la pregunta, tenemos,

=> $\frac{1}{2} \left| \begin{array}{cc} -2 & 0 & 1 \\ 0 & 4 & 1 \\ 0 & k & 1 \\ \end{array} \right|=4$

=> |−2(4−k) − 0 + 1(0)| = 8

=> −8 + 2k = ±8

=> −8 + 2k = 8 o −8 + 2k = −8

=> k = 8 o k = 0

Por lo tanto, el valor de k es 0 u 8.

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Encuentra el área del triángulo con vértices en los puntos:

(i) (3, 8), (−4, 2) y (5, −1)

(ii) (2, 7), (1, 1) y (10, 8)

(iii) (−1, −8), (−2, −3) y (3, 2)

(iv) (0, 0), (6, 0), (4, 3)

Pregunta 2. Utilizando los determinantes, demuestre que los siguientes puntos son colineales:

(i) (5, 5), (−5, 1) y (10, 7)

(ii) (1, −1), (2, 1) y (4, 5)

(iii) (3, −2), (8, 8) y (5, 2)

(iv) (2, 3), (−1, −2) y (5, 8)

Pregunta 3. Si los puntos (a, 0), (0, b) y (1, 1) son colineales, prueba que a + b = ab.

Pregunta 4. Utilizando los determinantes, demuestre que los puntos (a, b), (a’, b’) y (a – a’, b – b) son colineales si a b’ = a’ b.

Pregunta 5. Encuentra el valor de λ para que los puntos (1, −5), (−4, 5) y (λ, 7) sean colineales.

Pregunta 6. Encuentra el valor de x si el área de ∆ es de 35 cm cuadrados con vértices (x, 4), (2, −6) y (5, 4).

Pregunta 7. Usando determinantes, encuentra el área del triángulo cuyos vértices son (1, 4), (2, 3), (–5, –3). ¿Los puntos dados son colineales?

Pregunta 8. Usando determinantes, encuentra el área del triángulo con vértices (–3, 5), (3, –6), (7, 2).

Pregunta 9. Usando determinantes, encuentre el valor de k para que los puntos (k, 2–2k), (–k+1, 2k), (–4–k, 6–2k) puedan ser colineales.

Pregunta 10. Si los puntos (x, –2), (5, 2), (8, 8) son colineales, encuentra x usando determinantes.

Pregunta 11. Si los puntos (3, –2), (x, 2), (8, 8) son colineales, encuentra x usando determinantes.

Pregunta 12. Usando determinantes, encuentre la ecuación de

(i) la línea que une los puntos (1, 2) y (3, 6).

(ii) la línea que une los puntos (3, 1) y (9, 3).

Pregunta 13. Encuentra los valores de k

(i) si el área del triángulo cuyos vértices son (k, 0) (4, 0) (0, 2) es 4 unidades cuadradas.

(ii) si el área del triángulo cuyos vértices son (−2, 0) (0, 4) (0, k) es 4 unidades cuadradas.

Deja una respuesta Cancelar la respuesta