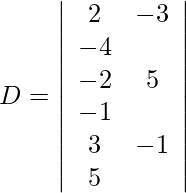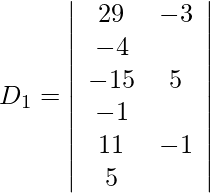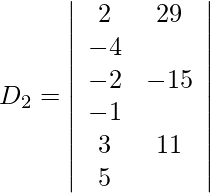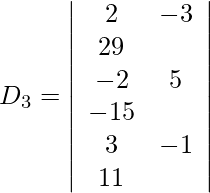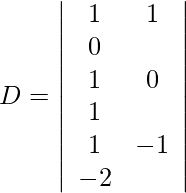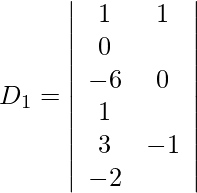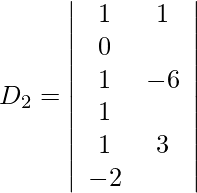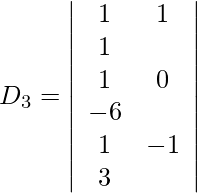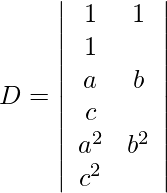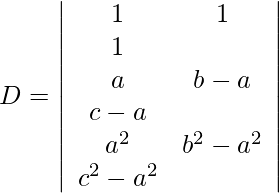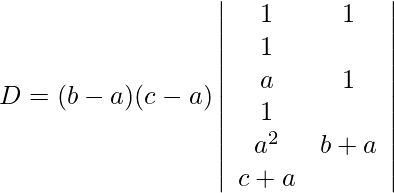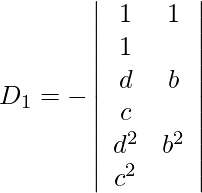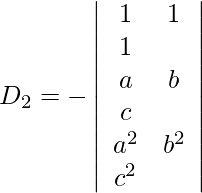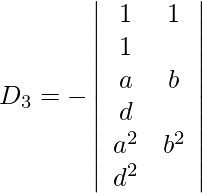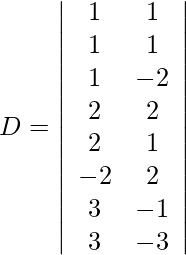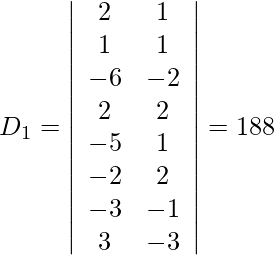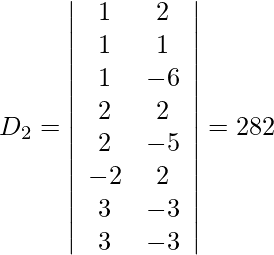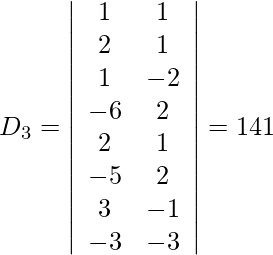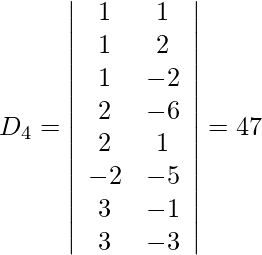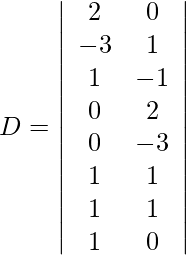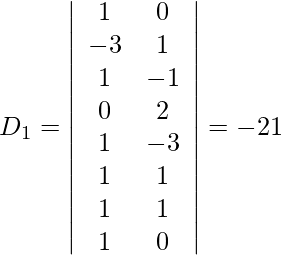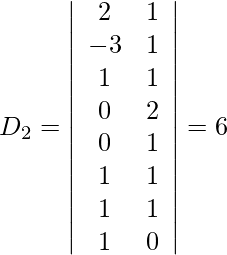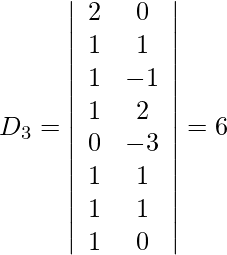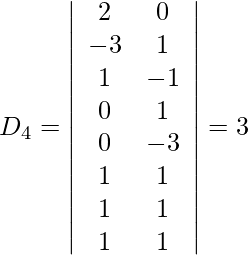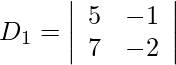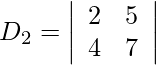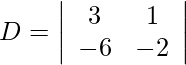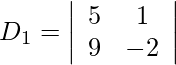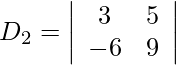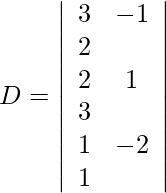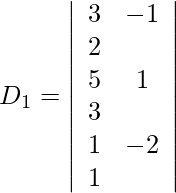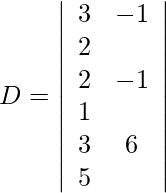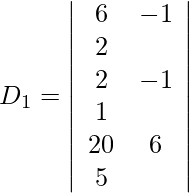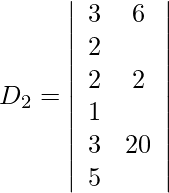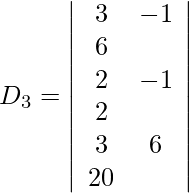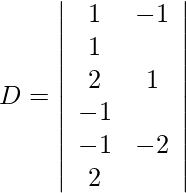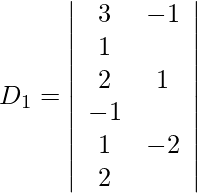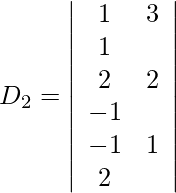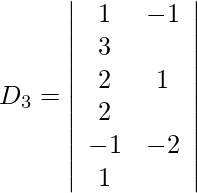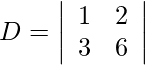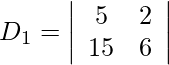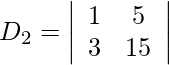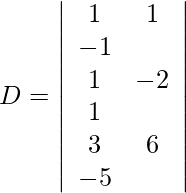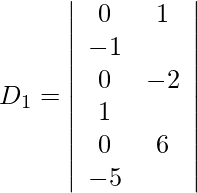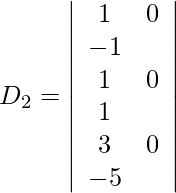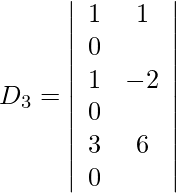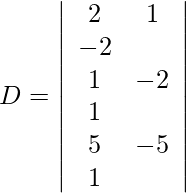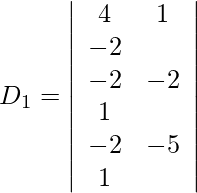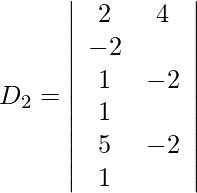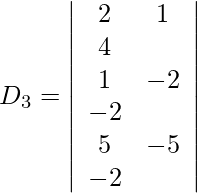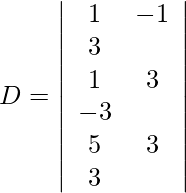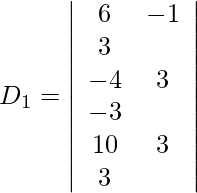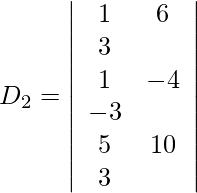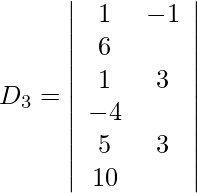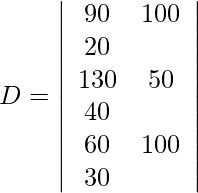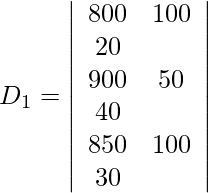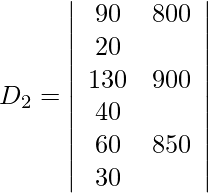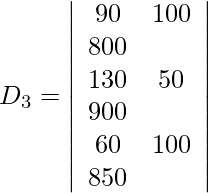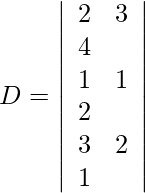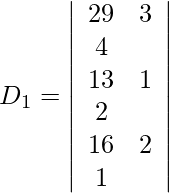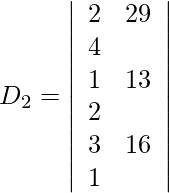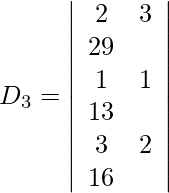Pregunta 17. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.
2x − 3y − 4z = 29
−2x + 5y − z = −15
3x − y + 5z = −11
Solución:
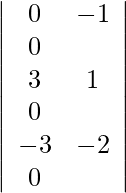
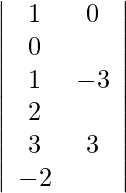
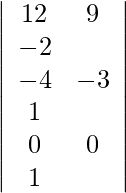
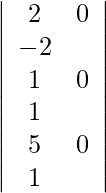
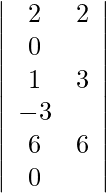
Usando la regla de Cramer, obtenemos,
Expandiendo a lo largo de R 1 , obtenemos,
= 2 (24) + 3 (−13) + 4 (-13)
= 48 − 21 – 52
= -25
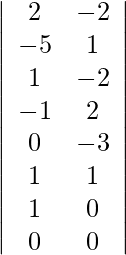
Además, obtenemos,
Expandiendo a lo largo de R 1 , obtenemos,
= 29 (24) + 3 (−64) + 4 (−40)
= 692 − 192 − 160
= 344
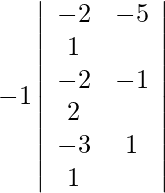
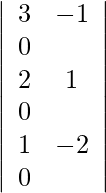
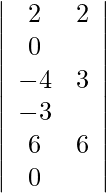
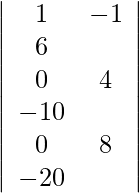
Expandiendo a lo largo de R 1 , obtenemos,
= 2 (−64) − 29 (−7) + 4 (23)
= −128 + 203 + 92
= 167
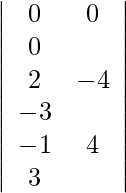
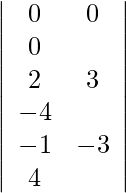
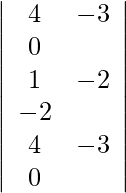
Expandiendo a lo largo de R 1 , obtenemos,
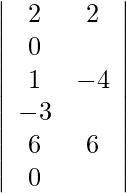
= 2 (40) + 3 (23) + 29 (−13)
= 80 + 69 − 377
= −228
Entonces, x = D 1 /D = -344/25
y = D 2 /D = -167/25
z = D 3 /D = 228/25
Por lo tanto, x = -344/25, y = -167/25 y z = 228/25.
Pregunta 18. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.
x + y = 1
x + z = −6
x – y – 2z = 3
Solución:
Usando la regla de Cramer, obtenemos,
= 1(1) – 1(-3)
= 1 + 3
= 4
Además, obtenemos,
Expandiendo a lo largo de R 1 , obtenemos,
= 1 (1) − 1 (9) + 0
= 1 − 9
= −8
Expandiendo a lo largo de R 1 , obtenemos,
= 1 (9) − 1 (−3)
= 9 + 3
= 12
Expandiendo a lo largo de R 1 , obtenemos,
= 1 (−6) − 1 (9) + 1 (−1)
= −6 − 9 − 1
= −16
Entonces, x = D 1 /D = -8/4 = -2
y = D 2 /D = 12/4 = 3
z = D 3 /D = -16/4 = -4
Por lo tanto, x = −2, y = 3 y z = −4.
Pregunta 19. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.
x + y + z + 1 = 0
hacha + por + cz + d = 0
un 2 x + segundo 2 y + c 2 z + re 2 = 0
Solución:
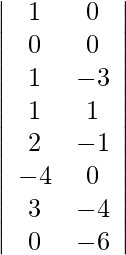
Usando la regla de Cramer, obtenemos,
do 2 -> do 2 – do 1 , do 3 -> do 3 – do 1
Tomando común (ba) de c 2 y (ca)c 3
1
Entonces, x = D 1 /D = /
y = re 2 /re = /
z = D 3 /D = /
Pregunta 20. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.
x + y + z + w = 2
x − 2y + 2z + 2w = −6
2x + y − 2z + 2w = −5
3x − y + 3z − 3w = −3
Solución:
Usando la regla de Cramer, obtenemos,
=
=
= −94
Además, obtenemos,
Entonces, x = D 1 /D = -188/94 = -2
y = D 2 /D = -282/-94 = 3
z = D 3 /D = -141/-94 = 3/2
w = D 4 /D = -47/94 = -1/2
Por lo tanto, x = −2, y = 3 y z = 3/2 y w = -1/2.
Pregunta 21. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.
2x – 3z + w = 1
x – y + 2w = 1
−3y + z + w = 1
x + y + z = −1
Solución:
Usando la regla de Cramer, obtenemos,
=
=
= −21
Además, obtenemos,
Entonces, x = D 1 /D = -21/-21 = 1
y = D 2 /D = -6/-21 = 2/7
z = D 3 /D = -6/-21 = 2/7
w = D 4 /D = -3/21 = -1/7
Por lo tanto, x = 1, y = 2/7 y z = 2/7 y w = -1/7.
Pregunta 22. Muestre que el siguiente sistema de ecuaciones lineales es inconsistente.
2x − y = 5
4x − 2y = 7
Solución:
Usando la regla de Cramer, obtenemos,
= −4 + 4
= 0
Además, obtenemos,
= − 10 + 7
= −3
= 14 − 20
= −6
Dado que D = 0 y D 1 y D 2 son distintos de cero, el sistema de ecuaciones dado es inconsistente.
Por lo tanto probado.
Pregunta 23. Muestre que el siguiente sistema de ecuaciones lineales es inconsistente.
3x + y = 5
−6x − 2y = 9
Solución:
Usando la regla de Cramer, obtenemos,
= −6 + 6
= 0
Además, obtenemos,
= −10 − 9
= −19
= 27 + 30
= 57
Dado que D = 0 y D 1 y D 2 son distintos de cero, el sistema de ecuaciones dado es inconsistente.
Por lo tanto probado.
Pregunta 24. Muestre que el siguiente sistema de ecuaciones lineales es inconsistente.
3x – y + 2z = 3
2x + y + 3z = 5
x − 2y − z = 1
Solución:
Usando la regla de Cramer, obtenemos,
Expandiendo a lo largo de R 1 , obtenemos
= 3 (5) + 1 (−5) + 2 (−5)
= 15 − 5 − 10
= 0
Además, obtenemos,
Expandiendo a lo largo de R 1 , obtenemos
= 3 (5) + 1 (−8) + 2 (−11)
= 15 − 8 − 22
= −15
Dado que D = 0 y D 1 son distintos de cero, el sistema de ecuaciones dado es inconsistente.
Por lo tanto probado.
Pregunta 25. Demuestra que el siguiente sistema de ecuaciones lineales es consistente y resuelve.
3x – y + 2z = 6
2x – y + z = 2
3x + 6y + 5z = 20
Solución:
Usando la regla de Cramer, obtenemos,
Expandiendo a lo largo de R 1 , obtenemos
= 3 (−11) + 1 (7) + 2 (15)
= −33 + 7 + 30
= 4
Además, obtenemos,
Expandiendo a lo largo de R 1 , obtenemos
= 6 (−11) + 1 (−10) + 2 (32)
= −66 − 10 + 64
= −12
Expandiendo a lo largo de R 1 , obtenemos
= 3 (−10) − 6 (7) + 2 (34)
= −30 − 42 + 68
= −4
Expandiendo a lo largo de R 1 , obtenemos
= 3 (−32) + 1 (34) + 6 (15)
= −96 + 34 + 90
= 28
Como D, D 1 , D 2 y D 3 son todos distintos de cero, el sistema de ecuaciones dado es consistente.
Entonces, x = D 1 /D = -12/4 = -3
y = D 2 /D = -4/4 = -1
z = D 3 /D = 28/4 = 7
Por lo tanto, x = −3, y = −1 y z = 7.
Pregunta 26. Demuestre que el siguiente sistema de ecuaciones lineales tiene un número infinito de soluciones.
x – y + z = 3
2x + y − z = 2
−x − 2y + 2z = 1
Solución:
Usando la regla de Cramer, obtenemos,
=
= 0
Además, obtenemos,
=
= 0
=
= 0
=
= 0
Como D, D 1 , D 2 y D 3 son todos cero, el sistema de ecuaciones dado tiene un número infinito de soluciones.
Por lo tanto probado.
Pregunta 27. Demuestre que el siguiente sistema de ecuaciones lineales tiene un número infinito de soluciones.
x + 2y = 5
3x + 2y = 15
Solución:
Usando la regla de Cramer, obtenemos,
= 6 − 6
= 0
Además, obtenemos,
= 30 − 30
= 0
= 15 − 15
= 0
Como D, D 1 y D 2 son todos cero, el sistema de ecuaciones dado tiene un número infinito de soluciones.
Por lo tanto probado.
Pregunta 28. Demuestre que el siguiente sistema de ecuaciones lineales tiene un número infinito de soluciones.
x + y − z = 0
x − 2y + z = 0
3x + 6y − 5z = 0
Solución:
Usando la regla de Cramer, obtenemos,
=
= 1 (6 − 6)
= 0
Además, obtenemos,
= 0
= 0
= 0
Como D, D 1 , D 2 y D 3 son todos cero, el sistema de ecuaciones dado tiene un número infinito de soluciones.
Por lo tanto probado.
Pregunta 29. Demuestre que el siguiente sistema de ecuaciones lineales tiene un número infinito de soluciones.
2x + y − 2z = 4
x − 2y + z = −2
5x − 5y + z = −2
Solución:
Usando la regla de Cramer, obtenemos,
=
= 1 (−36 + 36)
= 0
También obtenemos,
=
= 0
=
= 0
=
= 2 (−12 + 12)
= 0
Como D, D 1 , D 2 y D 3 son todos cero, el sistema de ecuaciones dado tiene un número infinito de soluciones.
Por lo tanto probado.
Pregunta 30. Demuestre que el siguiente sistema de ecuaciones lineales tiene un número infinito de soluciones.
x – y + 3z = 6
x + 3y − 3z = −4
5x + 3y + 3z = 10
Solución:
Usando la regla de Cramer, obtenemos,
=
= 3 (12 − 12)
= 0
También obtenemos,
=
= 3 (12 − 12)
= 0
=
= 3 (12 − 12)
= 0
=
= 1 (−80 + 80)
= 0
Como D, D 1 , D 2 y D 3 son todos cero, el sistema de ecuaciones dado tiene un número infinito de soluciones.
Por lo tanto probado.
Pregunta 31. Un vendedor tiene el siguiente registro de ventas durante tres meses de tres artículos A, B y C que tienen diferentes tasas de comisión.
| Mes | Venta de unidades | Comisión total (en Rs) | ||
|---|---|---|---|---|
| A | B | C | ||
| Ene | 90 | 100 | 20 | 800 |
| Feb | 130 | 50 | 40 | 900 |
| Mar | 60 | 100 | 30 | 850 |
Averigüe las tasas de comisión sobre los artículos A, B y C utilizando el método determinante.
Solución:
Sean x, y y z respectivamente las tasas de comisión sobre los artículos A, B y C.
De acuerdo con la pregunta, tenemos,
90x + 100y + 20z = 800
130x + 50y + 40z = 900
60x + 100y + 30z = 850
Usando la regla de Cramer, obtenemos,
=
= 50 (8500 − 12000)
= −175000
También obtenemos,
=
= 50 (50000 − 57000)
= −350000
=
= 20 (17500 − 52500)
= −700000
=
= 50 (161500 − 200000)
= −1925000
Entonces, x = D 1 /D = -350000/-175000 = 2
y = D 2 /D = -700000/-175000 = 4
z = D 3 /D = -1925000/-175000 = 11
Por tanto, las tasas de comisión de los artículos A, B y C son del 2%, 4% y 11% respectivamente.
Pregunta 32. Una empresa de automóviles utiliza tres tipos de acero S 1 , S 2 y S 3 para producir tres tipos de automóviles C 1 , C 2 y C 3 . A continuación se indican los requisitos de acero (en toneladas) para cada tipo de vagón.
| Acero | Coches | ||
|---|---|---|---|
| C 1 | C 2 | C 3 | |
| S 1 | 2 | 3 | 4 |
| S 2 | 1 | 1 | 2 |
| S 3 | 3 | 2 | 1 |
Usando la regla de Cramer, encuentre el número de autos de cada tipo que se pueden producir usando 29, 13 y 16 toneladas de acero de tres tipos respectivamente.
Solución:
Sean x, y y z el número de automóviles C 1 , C 2 y C 3 producidos respectivamente.
De acuerdo con la pregunta, tenemos,
2x + 3y + 4z = 29
x + y + 2z = 13
3x + 2y + z = 16
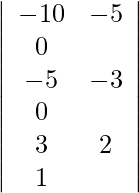
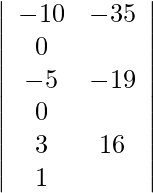
Usando la regla de Cramer, obtenemos,
=
= 1 (30 − 25)
= 5
También obtenemos,
=
= 1 (105 − 95)
= 10
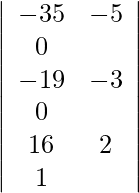
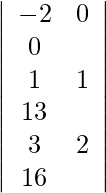
=
= 1 (190 − 175)
= 15
=
= −2 (16 − 26)
= 20
Entonces, x = D 1 /D = 10/5 = 2
y = D 2 /D = 15/5 = 3
z = D 3 /D = 20/5 = 4
Por lo tanto, el número de automóviles producidos del tipo C 1 , C 2 y C 3 son 2, 3 y 4.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA