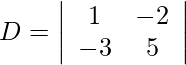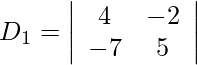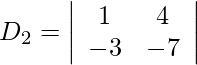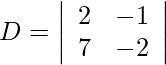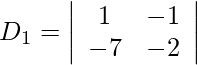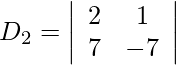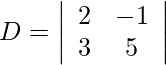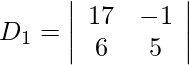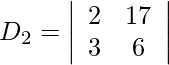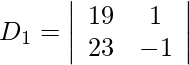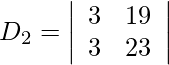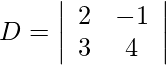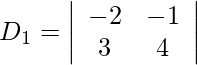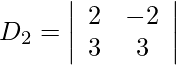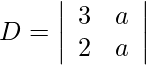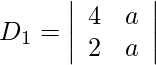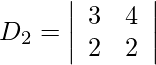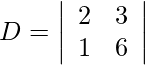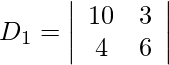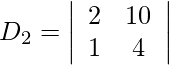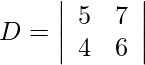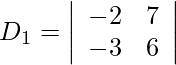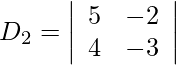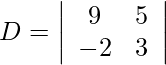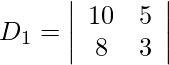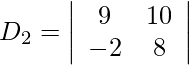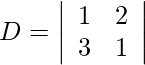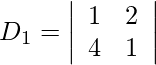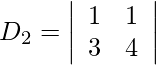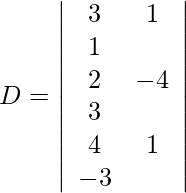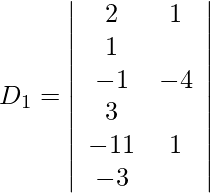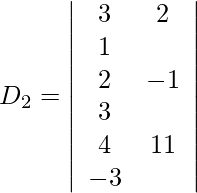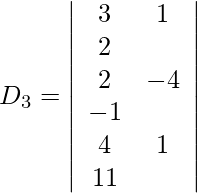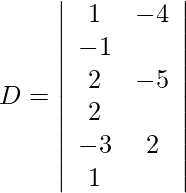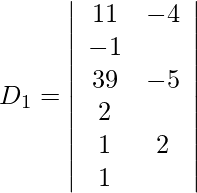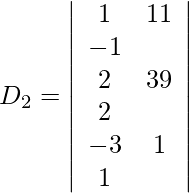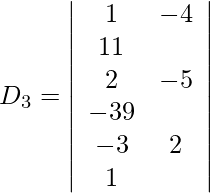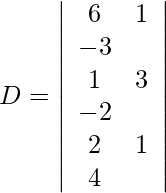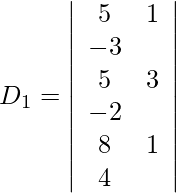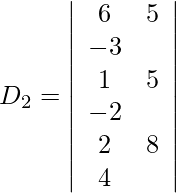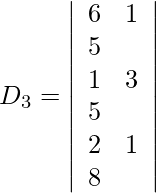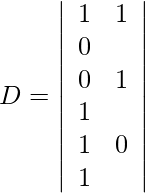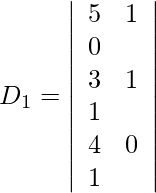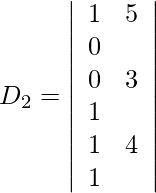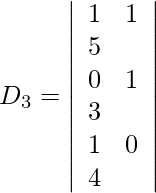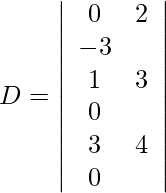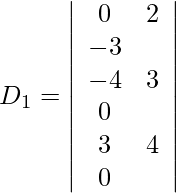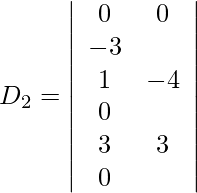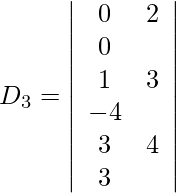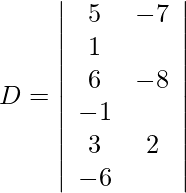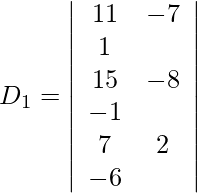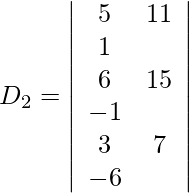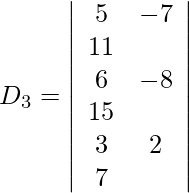Clase 12 Soluciones RD Sharma – Capítulo 6 Determinantes – Ejercicio 6.4

Pregunta 1. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

x-2y = 4

−3x + 5y = −7

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 1 & -2 \\ -3 & 5 \end{array} \right|$

= 5 − 6

= −1

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 4 & -2 \\ -7 & 5 \end{array} \right|$

= 20 − 14

= 6

$D_2=\left|\begin{array}{cc} 1 & 4 \\ -3 & -7 \end{array} \right|$

= −7 + 12

= 5

Entonces, x = D ₁ /D = 6/-1 = -6

Y y = D ₂ /D = 5/-1 = -5

Por lo tanto, x = −6 y y = −5.

Pregunta 2. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

2x – y = 1

7x – 2y = −7

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 2 & -1 \\ 7 & -2 \end{array} \right|$

= −4 + 7

= 3

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 1 & -1 \\ -7 & -2 \end{array} \right|$

= −2 − 7

= −9

$D_2=\left|\begin{array}{cc} 2 & 1 \\ 7 & -7 \end{array} \right|$

= −14 − 7

= −21

Entonces, x = D ₁ /D = -9/3 = -3

Y y = D ₂ /D = -21/3 = -7

Por lo tanto, x = −3 y y = −7.

Pregunta 3. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

2x – y = 17

3x + 5y = 6

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 2 & -1 \\ 3 & 5 \end{array} \right|$

= 10 + 3

= 13

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 17 & -1 \\ 6 & 5 \end{array} \right|$

= 85 + 6

= 91

$D_2=\left|\begin{array}{cc} 2 & 17 \\ 3 & 6 \end{array} \right|$

= 12 − 51

= −39

Entonces, x = D ₁ /D = 91/3 = 7

Y y = D ₂ /D = -39/13 = -3

Por lo tanto, x = 7 y y = −3.

Pregunta 4. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

3x + y = 19

3x – y = 23

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 3 & 1 \\ 3 & -1 \end{array} \right|$

= −3 − 3

= −6

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 19 & 1 \\ 23 & -1 \end{array} \right|$

= −19 − 23

= −42

$D_2=\left|\begin{array}{cc} 3 & 19 \\ 3 & 23 \end{array} \right|$

= 69 − 57

= 12

Entonces, x = D ₁ /D = -42/-6 = 7

Y y = D ₂ /D = 12/-6 = -2

Por lo tanto, x = 7 y y = −2.

Pregunta 5. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

2x – y = –2

3x + 4y = 3

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 2 & -1 \\ 3 & 4 \end{array} \right|$

= 8 + 3

= 11

Además, obtenemos,

$D_1=\left|\begin{array}{cc} -2 & -1 \\ 3 & 4 \end{array} \right|$

= −8 + 3

= −5

$D_2=\left|\begin{array}{cc} 2 & -2 \\ 3 & 3 \end{array} \right|$

= 6 + 6

= 12

Entonces, x = D ₁ /D = -5/11

Y y = D ₂ /D = 12/11

Por tanto, x = -5/11 ey = 12/11.

Pregunta 6. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

3x + ay = 4

2x + ay = 2, a ≠ 0

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 3 & a \\ 2 & a \end{array} \right|$

= 3a − 2a

= un

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 4 & a \\ 2 & a \end{array} \right|$

= 4a − 2a

= 2a

$D_2=\left|\begin{array}{cc} 3 & 4 \\ 2 & 2 \end{array} \right|$

= 6 − 8

= −2

Entonces, x = D ₁ /D = 2a/a = 2

Y y = D ₂ /D = -2/a

Por lo tanto, x = aey y = -2/a.

Pregunta 7. Resuelva el siguiente sistema de ecuación lineal por la regla de Cramer.

2x + 3y = 10

x + 6y = 4

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 2 & 3 \\ 1 & 6 \end{array} \right|$

= 12 − 3

= 9

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 10 & 3 \\ 4 & 6 \end{array} \right|$

= 60 − 12

= 48

$D_2=\left|\begin{array}{cc} 2 & 10 \\ 1 & 4 \end{array} \right|$

= 8 − 10

= −2

Entonces, x = D ₁ /D = 48/9 = 16/3

Y y = D ₂ /D = -2/9

Por tanto, x = 4/3 ey = -2/9.

Pregunta 8. Resuelva el siguiente sistema de ecuación lineal por la regla de Cramer.

5x + 7y = −2

4x + 6y = −3

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 5 & 7 \\ 4 & 6 \end{array} \right|$

= 30 − 28

= 2

Además, obtenemos,

$D_1=\left|\begin{array}{cc} -2 & 7 \\ -3 & 6 \end{array} \right|$

= −12 + 21

= 9

$D_2=\left|\begin{array}{cc} 5 & -2 \\ 4 & -3 \end{array} \right|$

= −15 + 8

= −7

Entonces, x = D ₁ /D = 9/2

Y y = D ₂ /D = -7/2

Por tanto, x = 9/2 ey = -7/2.

Pregunta 9. Resuelva el siguiente sistema de ecuación lineal por la regla de Cramer.

9x + 5y = 10

3y – 2x = 8

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 9 & 5 \\ -2 & 3 \end{array} \right|$

= 27 + 10

= 37

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 10 & 5 \\ 8 & 3 \end{array} \right|$

= 30 − 40

= −10

$D_2=\left|\begin{array}{cc} 9 & 10 \\ -2 & 8 \end{array} \right|$

= 72 + 20

= 92

Entonces, x = D ₁ /D = -10/37

Y y = D ₂ /D = 92/37

Por tanto, x = -10/37 ey = 92/37.

Pregunta 10. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

x + 2y = 1

3x + y = 4

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 1 & 2 \\ 3 & 1 \end{array} \right|$

= 1 − 6

= −5

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 1 & 2 \\ 4 & 1 \end{array} \right|$

= 1 − 8

= −7

$D_2=\left|\begin{array}{cc} 1 & 1 \\ 3 & 4 \end{array} \right|$

= 4 − 3

= 1

Entonces, x = D ₁ /D = -7/-5 = 7/5

Y y = D ₂ /D = -1/5

Por tanto, x = 7/5 ey = -1/5.

Pregunta 11. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

3x + y + z = 2

2x – 4y + 3z = −1

4x + y – 3z = −11

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 3 & 1 & 1 \\ 2 & -4 & 3 \\ 4 & 1 & -3 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 3 (12 − 3) + (−1) (−6 − 12) + 1 (2 + 16)

= 27 + 18 + 18

= 63

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 2 & 1 & 1 \\ -1 & -4 & 3 \\ -11 & 1 & -3 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 2 (12 − 3) + (−1) (3 + 33) + 1 (−1 − 44)

= 18 − 36 − 45

= −63

$D_2=\left|\begin{array}{cc} 3 & 2 & 1 \\ 2 & -1 & 3 \\ 4 & 11 & -3 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 3 (3 + 33) + (−2) (−6 − 12) + 1 (−22 + 4)

= 108 + 36 − 18

= 126

$D_3=\left|\begin{array}{cc} 3 & 1 & 2 \\ 2 & -4 & -1 \\ 4 & 1 & 11 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 3 (44 + 1) + (−1) (−22 + 4) + 2 (2 + 16)

= 135 + 18 + 36

= 189

Entonces, x = D ₁ /D = -63/63 = -1

y = D ₂ /D = 126/63 = 2

z = D ₃ /D = 189/63 = 3

Por lo tanto, x = −1, y = 2 y z = 3.

Pregunta 12. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

x-4y-z = 11

2x – 5y + 2z = 39

−3x + 2y + z = 1

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 1 & -4 & -1 \\ 2 & -5 & 2 \\ -3 & 2 & 1 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 1 (−5 − 4) + 4 (2 + 6) − 1 (4 − 15)

= −9 + 32 + 11

= 34

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 11 & -4 & -1 \\ 39 & -5 & 2 \\ 1 & 2 & 1 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 11 (−5 − 4) + 4 (39 − 2) − 1 (78 + 5)

= −99 + 148 − 83

= −34

$D_2=\left|\begin{array}{cc} 1 & 11 & -1 \\ 2 & 39 & 2 \\ -3 & 1 & 1 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 1 (39 − 2) − 11 (2 + 6) −1 (2 + 117)

= 37 − 88 − 119

= −170

$D_3=\left|\begin{array}{cc} 1 & -4 & 11 \\ 2 & -5 & -39 \\ -3 & 2 & 1 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 1 (−5 − 78) + 4 (2 + 117) + 11 (4 − 15)

= −83 + 476 − 121

= 272

Entonces, x = D ₁ /D = -34/34 = -1

y = D ₂ /D = -170/34 = -5

z = D ₃ /D = 272/34 = 8

Por lo tanto, x = −1, y = −5 y z = 8.

Pregunta 13. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

6x + y – 3z = 5

x + 3y – 2z = 5

2x + y + 4z = 8

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 6 & 1 & -3 \\ 1 & 3 & -2 \\ 2 & 1 & 4 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 6 (12 + 2) − 1 (4 + 4) − 3 (1 − 6)

= 84 − 8 + 15

= 91

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 5 & 1 & -3 \\ 5 & 3 & -2 \\ 8 & 1 & 4 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 5 (12 + 2) − 1 (20 + 16) − 3 (5 − 24)

= 70 − 36 + 57

= 91

$D_2=\left|\begin{array}{cc} 6 & 5 & -3 \\ 1 & 5 & -2 \\ 2 & 8 & 4 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 6 (20 + 16) − 5 (4 + 4) − 3 (8 − 10)

= 216 − 40 + 6

= 182

$D_3=\left|\begin{array}{cc} 6 & 1 & 5 \\ 1 & 3 & 5 \\ 2 & 1 & 8 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 6 (24 − 5) − 1 (8 − 10) + 5 (1 − 6)

= 114 + 2 − 25

= 91

Entonces, x = D ₁ /D = 91/91 = 1

y = D ₂ /D = 182/91 = 2

z = D ₃ /D = 92/92 =1

Por lo tanto, x = 1, y = 2 y z = 1.

Pregunta 14. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

x + y = 5

y + z = 3

x + z = 4

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 1 (1) − 1 (−1) + 0 (−1)

= 1 + 1

= 2

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 5 & 1 & 0 \\ 3 & 1 & 1 \\ 4 & 0 & 1 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 5 (1) − 1 (−1) + 0 (−4)

= 5 + 1 + 0

= 6

$D_2=\left|\begin{array}{cc} 1 & 5 & 0 \\ 0 & 3 & 1 \\ 1 & 4 & 1 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 1 (−1) − 5 (−1) + 0 (−3)

= −1 + 5 + 0

= 4

$D_3=\left|\begin{array}{cc} 1 & 1 & 5 \\ 0 & 1 & 3 \\ 1 & 0 & 4 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 1 (4) − 1 (−3) + 5 (−1)

= 4 + 3 − 5

= 2

Entonces, x = D ₁ /D = 6/2 = 3

y = re ₂ / re = 4/2 = 2

z = D ₃ /D = 2/2 = 1

Por lo tanto, x = 3, y = 2 y z = 1.

Pregunta 15. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

2y – 3z = 0

x + 3y = −4

3x + 4y = 3

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 0 & 2 & -3 \\ 1 & 3 & 0 \\ 3 & 4 & 0 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 0 (0) − 2 (0) − 3 (−5)

= 0 − 0 + 15

= 15

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 0 & 2 & -3 \\ -4 & 3 & 0 \\ 3 & 4 & 0 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 0 (0) − 2 (0) − 3 (−25)

= 0 − 0 + 75

= 75

$D_2=\left|\begin{array}{cc} 0 & 0 & -3 \\ 1 & -4 & 0 \\ 3 & 3 & 0 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 0 (0) − 0 (0) − 3 (15)

= 0 − 0 − 45

= −45

$D_3=\left|\begin{array}{cc} 0 & 2 & 0 \\ 1 & 3 & -4 \\ 3 & 4 & 3 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 0 (25) − 2 (15) + 0 (1)

= 0 − 30 + 0

= −30

Entonces, x = D ₁ /D = 75/15 = 5

y = D ₂ /D = -45/15 = -3

z = D ₃ /D = -30/15 = -2

Por lo tanto, x = 5, y = −3 y z = −2.

Pregunta 16. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

5x – 7y + z = 11

6x – 8y – z = 15

3x + 2y – 6z = 7

Solución:

Usando la regla de Cramer, obtenemos,

$D=\left|\begin{array}{cc} 5 & -7 & 1 \\ 6 & -8 & -1 \\ 3 & 2 & -6 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 5 (50) + 7 (−33) + 1 (36)

= 250 − 231 + 36

= 55

Además, obtenemos,

$D_1=\left|\begin{array}{cc} 11 & -7 & 1 \\ 15 & -8 & -1 \\ 7 & 2 & -6 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 11 (50) + 7 (−83) + 1 (86)

= 550 − 581 + 86

= 55

$D_2=\left|\begin{array}{cc} 5 & 11 & 1 \\ 6 & 15 & -1 \\ 3 & 7 & -6 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 5 (−83) − 11 (−33) + 1 (−3)

= −415 + 363 − 3

= −55

$D_3=\left|\begin{array}{cc} 5 & -7 & 11 \\ 6 & -8 & 15 \\ 3 & 2 & 7 \end{array} \right|$

Expandiendo a lo largo de R ₁ , obtenemos,

= 5 (−86) + 7 (−3) + 11 (36)

= −430 − 21 + 396

= −55

Entonces, x = D ₁ /D = 55/55 = 1

y = D ₂ /D = -55/55 = -1

z = D ₃ /D = -55/55 = -1

Por lo tanto, x = 1, y = −1 y z = −1.

Publicación traducida automáticamente

Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

x-2y = 4

−3x + 5y = −7

Pregunta 2. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

2x – y = 1

7x – 2y = −7

Pregunta 3. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

2x – y = 17

3x + 5y = 6

Pregunta 4. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

3x + y = 19

3x – y = 23

Pregunta 5. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

2x – y = –2

3x + 4y = 3

Pregunta 6. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

3x + ay = 4

2x + ay = 2, a ≠ 0

Pregunta 7. Resuelva el siguiente sistema de ecuación lineal por la regla de Cramer.

2x + 3y = 10

x + 6y = 4

Pregunta 8. Resuelva el siguiente sistema de ecuación lineal por la regla de Cramer.

5x + 7y = −2

4x + 6y = −3

Pregunta 9. Resuelva el siguiente sistema de ecuación lineal por la regla de Cramer.

9x + 5y = 10

3y – 2x = 8

Pregunta 10. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

x + 2y = 1

3x + y = 4

Pregunta 11. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

3x + y + z = 2

2x – 4y + 3z = −1

4x + y – 3z = −11

Pregunta 12. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

x-4y-z = 11

2x – 5y + 2z = 39

−3x + 2y + z = 1

Pregunta 13. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

6x + y – 3z = 5

x + 3y – 2z = 5

2x + y + 4z = 8

Pregunta 14. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

x + y = 5

y + z = 3

x + z = 4

Pregunta 15. Resuelve el siguiente sistema de ecuaciones lineales por la regla de Cramer.

2y – 3z = 0

x + 3y = −4

3x + 4y = 3

Pregunta 16. Resuelva el siguiente sistema de ecuaciones lineales por la regla de Cramer.

5x – 7y + z = 11

6x – 8y – z = 15

3x + 2y – 6z = 7

Deja una respuesta Cancelar la respuesta