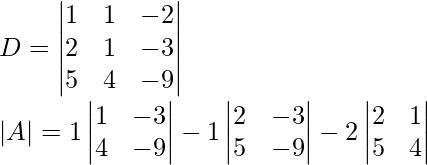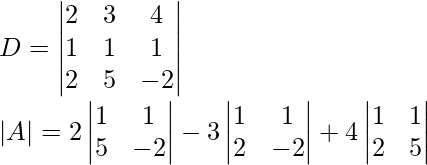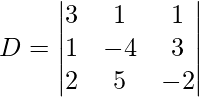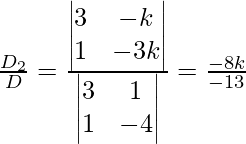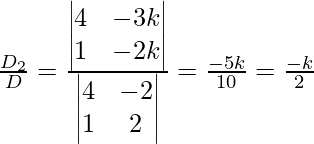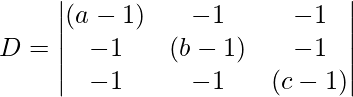Pregunta 1. Resuelve cada uno de los siguientes sistemas de ecuaciones lineales homogéneas:
x + y – 2z = 0
2x + y – 3z =0
5x + 4y – 9z = 0
Solución:
Dado:
x + y – 2z = 0
2x + y – 3z =0
5x + 4y – 9z = 0
Este sistema de ecuaciones se puede expresar en forma de array AX = B
Ahora encuentra el determinante,
= 1(1 × (-9) – 4 × (-3)) – 1(2 × (-9) – 5 × (-3)) – 2(4 × 2 – 5 × 1)
= 1(-9 + 12) – 1(-18 + 15) – 2(8 – 5)
= 1 × 3 – 1 × (-3) – 2 × 3
= 3 + 3 – 6
= 0
Entonces, D = 0, eso significa que este sistema de ecuaciones tiene una solución infinita.
Ahora,
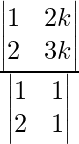
Sea z = k
⇒ x + y = 2k
Y 2x + y = 3k
Ahora usando la regla de Cramer
x =
x =
x =
x = k
Similarmente,
y =
y =
y =
y = k
Por lo tanto,
x = y = z = k.
Pregunta 2. Resuelve cada uno de los siguientes sistemas de ecuaciones lineales homogéneas:
2x + 3y + 4z = 0
x + y + z = 0
2x + 5y – 2z = 0
Solución:
2x + 3y + 4z = 0
x + y + z = 0
2x + 5y – 2z = 0
Este sistema de ecuaciones se puede expresar en forma de array AX = B
Encuentra el determinante
= 2(1 × (-2) – 1 × 5) – 3(1 × (-2) – 2 × 1) + 4(1 × 5 – 2 × 1)
= 2(-2 – 5) – 3(-2 – 2) + 4(5 – 2)
= 2 × (-7) – 3 × (-4) + 4 × 3
= -14 + 12 + 12
= -10
Por lo tanto, D ≠ 0, por lo que el sistema de ecuaciones tiene solución trivial.
Por lo tanto, el sistema de ecuaciones solo tiene solución cuando x = y = z = 0.
Pregunta 3. Resuelva cada uno de los siguientes sistemas de ecuaciones lineales homogéneas:
3x + y + z = 0
x – 4y + 3z = 0
2x +5y – 2z = 0
Solución:
Dado:
3x + y + z = 0
x – 4y + 3z = 0
2x +5y – 2z = 0
Este sistema de ecuaciones se puede expresar en forma de array AX = B
Encuentra el determinante
= 3(8 – 15) – 1(-2 – 6) + 1(13)
= -21 + 8 + 13
= 0
Entonces, el sistema tiene infinitas soluciones:
Sea z = k,
Asi que,
3x + y = -k
x – 4y = -3k
Ahora,
x =
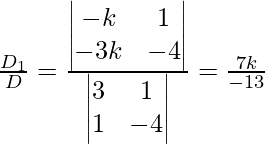
y =
x =
y =
z = k
y sus valores satisfacen la ecuación 3
Por lo tanto, x = -7k, y = 8k, z = 13k
Pregunta 4. Encuentra los valores reales de λ para los cuales el siguiente sistema de ecuaciones lineales tiene soluciones no triviales
2λx – 2y + 3z = 0
x + λy + 2z = 0
2x + λz = 0
Solución:
Encontrar el determinante
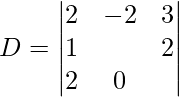
= 3λ 3 + 2λ – 8 – 6λ
= 2λ 3 – 4λ – 8
Que se satisface con λ = 2 {para soluciones no triviales λ =2}
Ahora sea z = k
4x – 2y = -3k
x + 2y = -3k
x =
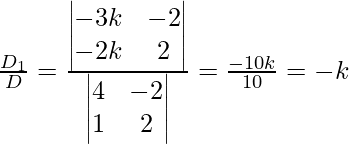
y =
Por lo tanto, la solución es x = -k, y =
, z = k
Pregunta 5. Si a, b, c son números reales distintos de cero y si el sistema de ecuaciones
(a – 1)x = y + z
(b – 1) y = z + x
(c – 1)z = x + y
tiene una solución no trivial, luego demuestre que ab + bc + ca = abc
Solución:
Encontrar el determinante
Ahora para una solución no trivial, D = 0
0 = (a – 1)[(b – 1)(c – 1) – 1]+1[-c + 1 – 1] + [-c + 1 – 1] – [ 1 + b – 1]
0 = (a – 1)[bc – b – c + 1 – 1] – c – b
0 = abc – ab -ac + b + c – c – b
ab + bc + ac = abc
Por lo tanto probado
Publicación traducida automáticamente
Artículo escrito por sudhasinghsudha90 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA