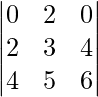
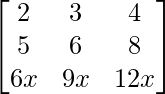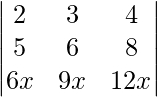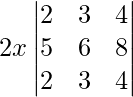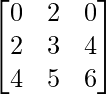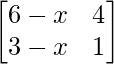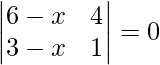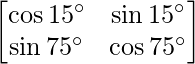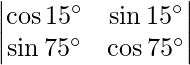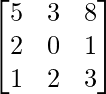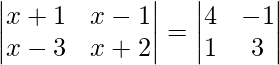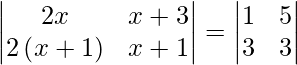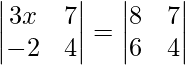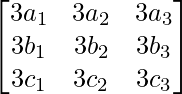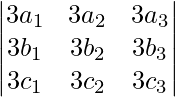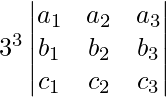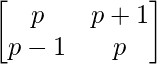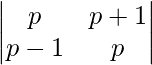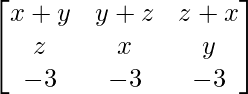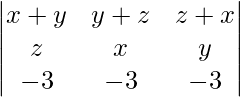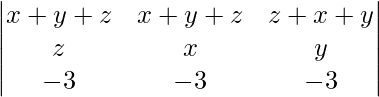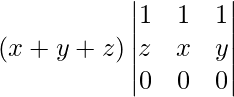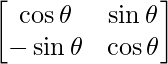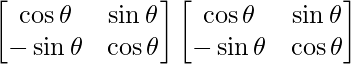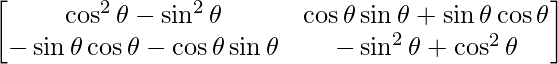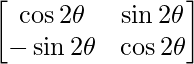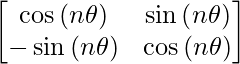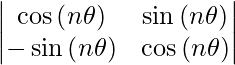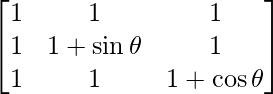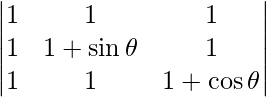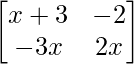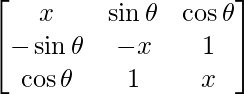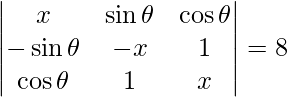Clase 12 RD Sharma Solutions – Capítulo 6 Determinantes Ejercicio Ej. 6.6 | conjunto 3

Posted on by Rudeus Greyrat

Pregunta 38. Escribe el valor del determinante 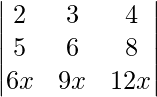 \begin{vmatrix}2 & 3 & 4 \\ 5 & 6 & 8 \\ 6x & 9x & 12x\end{vmatrix} .

Solución:

 Tenemos,

un = \begin{bmatrix}2 & 3 & 4 \\ 5 & 6 & 8 \\ 6x & 9x & 12x\end{bmatrix}

|A| = \begin{vmatrix}2 & 3 & 4 \\ 5 & 6 & 8 \\ 6x & 9x & 12x\end{vmatrix}

Al tomar 2x común de R 3 obtenemos,

|A| = 2x\begin{vmatrix}2 & 3 & 4 \\ 5 & 6 & 8 \\ 2 & 3 & 4\end{vmatrix}

Como R 1 y R 3 son idénticos obtenemos

|A| = 0

Por lo tanto, el valor del determinante es 0.

Pregunta 39. Si |A| = 2, donde A es una array de 2 × 2, encuentre |adj A|.

Solución:

Dado que |A| = 2 y el orden de la array A es 2 x 2

Como sabemos que |adj A| = |A| n-1

Aquí el valor de n es 2

Asi que, 

|adj A| = |2| 2-1

= 2

Por lo tanto, el valor de |adj A| es 2

Pregunta 40. ¿Cuál es el valor del determinante 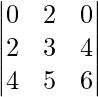 \begin{vmatrix}0 & 2 & 0 \\ 2 & 3 & 4 \\ 4 & 5 & 6\end{vmatrix} ?

Solución:

Tenemos,

un = \begin{bmatrix}0 & 2 & 0 \\ 2 & 3 & 4 \\ 4 & 5 & 6\end{bmatrix}

|A| = \begin{vmatrix}0 & 2 & 0 \\ 2 & 3 & 4 \\ 4 & 5 & 6\end{vmatrix}

= 0(18 – 20) – 2(12 – 16) + 0(10 – 12) 

= 0 + 8 + 0

= 8

Por lo tanto, el valor del determinante es 8.

Pregunta 41. ¿Para qué valor de x la array es 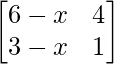 \begin{bmatrix}6 - x & 4 \\ 3 - x & 1\end{bmatrix}  singular?

Solución:

Como sabemos, una array es array singular, cuando el valor de su determinante es 0.

Dado que,

un = \begin{bmatrix}6 - x & 4 \\ 3 - x & 1\end{bmatrix}

Asi que, 

|A| = \begin{vmatrix}6 - x & 4 \\ 3 - x & 1\end{vmatrix} = 0

=> \begin{vmatrix}6 - x & 4 \\ 3 - x & 1\end{vmatrix} = 0

=> (6 – x) – 4(3 – x) = 0

=> 6 – x – 12 + 4x = 0

=> 3x – 6 = 0  

=> 3x = 6

=> x = 6/3

=> x = 2

Por lo tanto, el valor de x es 2.

Pregunta 42. Una array A de orden 3 × 3 es tal que |A| = 4. Encuentra el valor de |2 A|.

Solución:

Tenemos,

Una array A es de orden 3 × 3 por lo que el valor de n es 3.

Y |A| = 4.

Como la conocemos,

=> |KA| = Kn | A|

Asi que, 

|2A| = 2 3 (4)

= 8 (4)

= 32

Por lo tanto, el valor de |2 A| es 32

Pregunta 43. Evaluar: 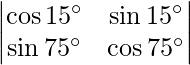 \begin{vmatrix}\cos 15^\circ & \sin 15^\circ \\ \sin 75^\circ & \cos 75^\circ\end{vmatrix} .

Solución:

Tenemos,

un = \begin{bmatrix}\cos 15^\circ & \sin 15^\circ \\ \sin 75^\circ & \cos 75^\circ\end{bmatrix}

|A| = \begin{vmatrix}\cos 15^\circ & \sin 15^\circ \\ \sin 75^\circ & \cos 75^\circ\end{vmatrix}

= cos 15° cos 75° – sen 15° sen 75°

Como cos A cos B – sen A sen B = cos (A + B), obtenemos 

= coseno (15° + 75°) 

= cos 90°

= 0

Pregunta 44. Si A = 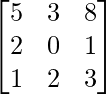 \begin{bmatrix}5 & 3 & 8 \\ 2 & 0 & 1 \\ 1 & 2 & 3\end{bmatrix} , escribe el cofactor del elemento a 32 .

Solución:

Tenemos, 

un = \begin{bmatrix}5 & 3 & 8 \\ 2 & 0 & 1 \\ 1 & 2 & 3\end{bmatrix}

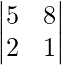
Entonces, el menor de 32 es,

METRO 32 = \begin{vmatrix}5 & 8 \\ 2 & 1\end{vmatrix}

= 5 – 16 

= -11  

Ahora, el cofactor de un 32 es,

UN 32 = (−1) 3+2 METRO 32 

= 11

Por tanto, el cofactor del elemento a 32 es 11.

Pregunta 45. Si 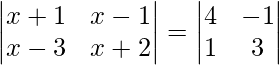 \begin{vmatrix}x + 1 & x - 1 \\ x - 3 & x + 2\end{vmatrix} = \begin{vmatrix}4 & - 1 \\ 1 & 3\end{vmatrix} , entonces escribe el valor de x.

Solución:

Tenemos,

\begin{vmatrix}x + 1 & x - 1 \\ x - 3 & x + 2\end{vmatrix} = \begin{vmatrix}4 & - 1 \\ 1 & 3\end{vmatrix}

Al expandir los determinantes de ambos lados, obtenemos

=> (x + 1) (x + 2) – (x – 1) (x – 3) = 12 + 1

=> x2 + 3x + 2 – x2 + 4x – 3 = 13

=> 7x – 1 = 13

=> 7x = 14

=> x = 2 

Por lo tanto, el valor de x es 2.

Pregunta 46. Si 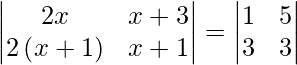 \begin{vmatrix}2x & x + 3 \\ 2\left( x + 1 \right) & x + 1\end{vmatrix} = \begin{vmatrix}1 & 5 \\ 3 & 3\end{vmatrix} , entonces escribe el valor de x.

Solución:

Se nos da,

=> \begin{vmatrix}2x & x + 3 \\ 2\left( x + 1 \right) & x + 1\end{vmatrix} = \begin{vmatrix}1 & 5 \\ 3 & 3\end{vmatrix}

Al expandir los determinantes de ambos lados, obtenemos

=> (2x) (x + 1) – 2 (x + 1) (x + 3) = 3 – 15  

=> (x + 1) (2x – 2x – 6) = -12 

=> -6x – 6 = – 12  

=> -6x = -6

=> x = 1

Por lo tanto, el valor de x es 1. 

Pregunta 47. Si 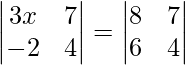 \begin{vmatrix}3x & 7 \\ - 2 & 4\end{vmatrix} = \begin{vmatrix}8 & 7 \\ 6 & 4\end{vmatrix} , encuentra el valor de x.

Solución:

Tenemos,

=> \begin{vmatrix}3x & 7 \\ - 2 & 4\end{vmatrix} = \begin{vmatrix}8 & 7 \\ 6 & 4\end{vmatrix}

Al expandir los determinantes de ambos lados, obtenemos

=> 12x + 14 = 32 – 42  

=> 12x + 14 = -10

=> 12x = -24

=> x = -24/12  

=> x = -2

Por lo tanto, el valor de x es -2. 

Pregunta 48. Si 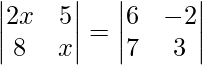 \begin{vmatrix}2x & 5 \\ 8 & x\end{vmatrix} = \begin{vmatrix}6 & - 2 \\ 7 & 3\end{vmatrix} , escribe el valor de x.

Solución:

Aquí tenemos,

=> \begin{vmatrix}2x & 5 \\ 8 & x\end{vmatrix} = \begin{vmatrix}6 & - 2 \\ 7 & 3\end{vmatrix}  

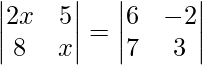
Al expandir los determinantes de ambos lados, obtenemos

=> 2x 2 – 40 = 18 + 14  

=> 2×2 – 40 = 32

=> 2×2 = 72  

=>x2 = 72/2

=>x2 = 36

=> x = ±6

Por lo tanto, el valor de x es ±6.

Pregunta 49. Si A es una array de 3 × 3, |A| ≠ 0 y |3A| = k |A| luego escribe el valor de k.

Solución:

Se nos da,

A es una array de 3 × 3.

También |A| ≠ 0 y |3A| = k |A|.

Consideremos A = \begin{bmatrix}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{bmatrix}   

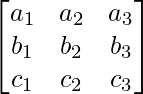
3A = \begin{bmatrix}3 a_1 & 3 a_2 & 3 a_3 \\ 3 b_1 & 3 b_2 & 3 b_3 \\ 3 c_1 & 3 c_2 & 3 c_3\end{bmatrix}

|3A| = \begin{vmatrix}3 a_1 & 3 a_2 & 3 a_3 \\ 3 b_1 & 3 b_2 & 3 b_3 \\ 3 c_1 & 3 c_2 & 3 c_3\end{vmatrix}

Al sacar 3 comunes de cada fila obtenemos,

= 3^3 \begin{vmatrix}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{vmatrix}

= 27 |A|

Por lo tanto, el valor de k es 27. 

Pregunta 50. Escribe el valor del determinante 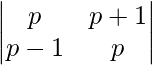 \begin{vmatrix}p & p + 1 \\ p - 1 & p\end{vmatrix} .

Solución:

Tenemos,

un = \begin{bmatrix}p & p + 1 \\ p - 1 & p\end{bmatrix}

|A| = \begin{vmatrix}p & p + 1 \\ p - 1 & p\end{vmatrix}

Al desarrollar el determinante que tenemos,

= pag 2 – (pag + 1) (pag – 1)

= pag 2 – (pag 2 – 1)

= pag 2 – pag 2 + 1

= 1

Por lo tanto, el valor del determinante es 1.

Pregunta 51. Escribe el valor del determinante 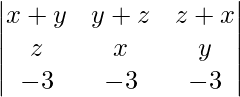 \begin{vmatrix}x + y & y + z & z + x \\ z & x & y \\ - 3 & - 3 & - 3\end{vmatrix} .

Solución:

Tenemos,

un = \begin{bmatrix}x + y & y + z & z + x \\ z & x & y \\ - 3 & - 3 & - 3\end{bmatrix}

|A| = \begin{vmatrix}x + y & y + z & z + x \\ z & x & y \\ - 3 & - 3 & - 3\end{vmatrix}

Al aplicar R 1 -> R 1 + R 2 obtenemos,

= \begin{vmatrix}x + y + z & x + y + z & z + x + y \\ z & x & y \\ - 3 & - 3 & - 3\end{vmatrix}

Al tomar x + y + z común de R 1 tenemos,

= \left( x + y + z \right)\begin{vmatrix}1 & 1 & 1 \\ z & x & y \\ - 3 & - 3 & - 3\end{vmatrix}  

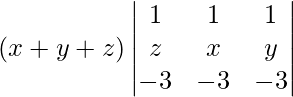
Al aplicar R 3 -> R 3 + 3 R 1 obtenemos,

= \left( x + y + z \right)\begin{vmatrix}1 & 1 & 1 \\ z & x & y \\ - 3 & - 3 & - 3\end{vmatrix}  

= \left( x + y + z \right)\begin{vmatrix}1 & 1 & 1 \\ z & x & y \\ 0 & 0 & 0\end{vmatrix}

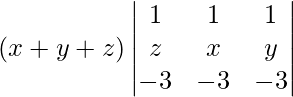
Al expandir a lo largo de la última fila obtenemos,

= 0

Por lo tanto, el valor del determinante es 0.

Pregunta 52. Si A = 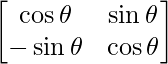 \begin{bmatrix}\cos\theta & \sin\theta \\ - \sin\theta & \cos\theta\end{bmatrix} , entonces para cualquier número natural, encuentra el valor de Det(A n ).

Solución:

Dado que, A = \begin{bmatrix}\cos\theta & \sin\theta \\ - \sin\theta & \cos\theta\end{bmatrix}

=> Un 2 = \begin{bmatrix}\cos\theta & \sin\theta \\ - \sin\theta & \cos\theta\end{bmatrix}\begin{bmatrix}\cos\theta & \sin\theta \\ - \sin\theta & \cos\theta\end{bmatrix}

= \begin{bmatrix}\cos^2 \theta - \sin^2 \theta & \cos\theta\sin\theta + \sin\theta\cos\theta \\ - \sin\theta\cos\theta - \cos\theta\sin\theta & - \sin^2 \theta + \cos^2 \theta\end{bmatrix}

= \begin{bmatrix}\cos2\theta & \sin2\theta \\ - \sin2\theta & \cos2\theta\end{bmatrix}

Del mismo modo, A n = \begin{bmatrix}\cos\left( n\theta \right) & \sin\left( n\theta \right) \\ - \sin\left( n\theta \right) & \cos\left( n\theta \right)\end{bmatrix}

Asi que,  

|Un norte | = \begin{vmatrix}\cos\left( n\theta \right) & \sin\left( n\theta \right) \\ - \sin\left( n\theta \right) & \cos\left( n\theta \right)\end{vmatrix}

= (cos nθ) (cos nθ) + (sen nθ) (sen nθ)

= cos 2 (nθ) + sen 2 (nθ)

= 1

Por lo tanto, Det(A n ) = 1.

Pregunta 53. Encuentra el valor máximo de 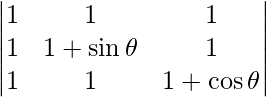 \begin{vmatrix}1 & 1 & 1 \\ 1 & 1 + \sin \theta & 1 \\ 1 & 1 & 1 + \cos \theta\end{vmatrix} .

Solución:

Tenemos,

un = \begin{bmatrix}1 & 1 & 1 \\ 1 & 1 + \sin \theta & 1 \\ 1 & 1 & 1 + \cos \theta\end{bmatrix}

|A| = \begin{vmatrix}1 & 1 & 1 \\ 1 & 1 + \sin \theta & 1 \\ 1 & 1 & 1 + \cos \theta\end{vmatrix}

Al aplicar R 2 -> R 2 – R 1 y R 3 -> R 3 – R 1 , obtenemos

|A| = \begin{vmatrix}1 & 1 & 1 \\ 0 & \sin\theta & 0 \\ 0 & 0 & \cos\theta\end{vmatrix}   

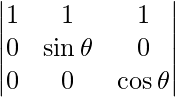
= sen θ cos θ

= (sen 2θ)/2

Sabemos que −1 ≤ sin2θ ≤ 1.

Entonces, el valor máximo de |A| = (1/2) (1) 

= 1/2

Por lo tanto, el valor máximo es 1/2.

Pregunta 54. Si x ∈ N y 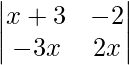 \begin{vmatrix}x + 3 & - 2 \\ - 3x & 2x\end{vmatrix}  = 8, entonces encuentra el valor de x.

Solución:

Aquí tenemos,

un = \begin{bmatrix}x + 3 & - 2 \\ - 3x & 2x\end{bmatrix}

|A| = 8

En la expansión obtenemos,

=> (x + 3) (2x) – (-2) (-3x) = 8

=> 2×2 + 6x – 6x = 8

=> 2×2 = 8

=> 2x 2 – 8 = 0

=> x 2 – 4 = 0

=> x2 = 4

Como x ∈ N, obtenemos

=> x = 2 

Por lo tanto, el valor de x es 2.

Pregunta 55. Si 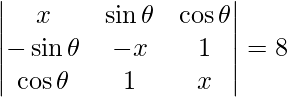 \begin{vmatrix}x & \sin \theta & \cos \theta \\ - \sin \theta & - x & 1 \\ \cos \theta & 1 & x\end{vmatrix} = 8 , escribe el valor de x.

Solución:

Tenemos,

un = \begin{bmatrix}x & \sin \theta & \cos \theta \\ - \sin \theta & - x & 1 \\ \cos \theta & 1 & x\end{bmatrix}

|A| = \begin{vmatrix}x & \sin \theta & \cos \theta \\ - \sin \theta & - x & 1 \\ \cos \theta & 1 & x\end{vmatrix} = 8

=> \begin{vmatrix}x & \sin \theta & \cos \theta \\ - \sin \theta & - x & 1 \\ \cos \theta & 1 & x\end{vmatrix} = 8

Al expandir a lo largo de R 1 , obtenemos

=> x (-x 2 – 1) – sen θ (-x sen θ – cos θ) + cos θ (-sen θ + x cos θ) = 8

=> -x 3 – x + x sen 2 θ + sen θ cos θ – sen θ cos θ + x cos 2 θ = 8

=> -x 3 – x + x (sen 2 θ + cos 2 θ) = 8

=> -x 3 – x + x = 8

=> x 3 + 8 = 0

=> x = -2

Por lo tanto, el valor de x es -2.

Pregunta 56. Si A es una array invertible de 3 × 3, ¿cuál será el valor de k si det(A –1 ) = (det A) k .

Solución:

Dado que A es una array invertible de 3 × 3.

Entonces, sabemos que

A^{- 1} = \frac{Adj A}{\left| A \right|}

Por lo tanto obtenemos,

=> \left| A^{- 1} \right| = \frac{\left| Adj A \right|}{\left| A \right|}

Como sabemos que, \left|adj\left( A \right) \right| = \left| A \right|^{n - 1}

= \frac{\left| A \right|^{3 - 1}}{\left| A \right|}

= \frac{\left| A \right|^2}{\left| A \right|}

= |A|

|A -1 | = | Ak |, obtenemos

=> k = 1

Por lo tanto, el valor de k es 1.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *