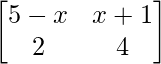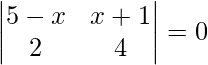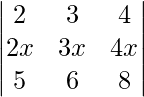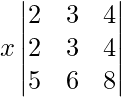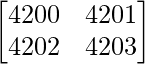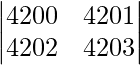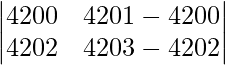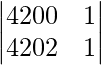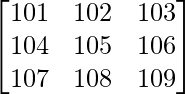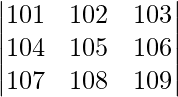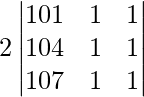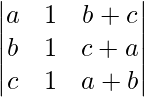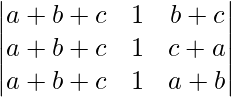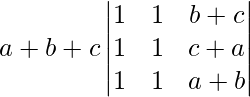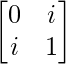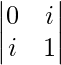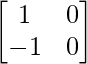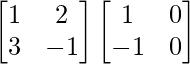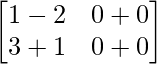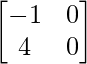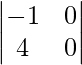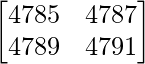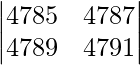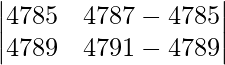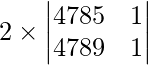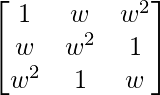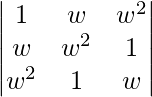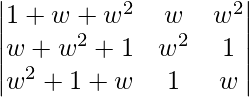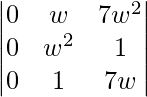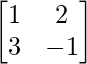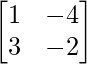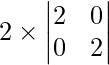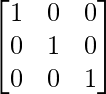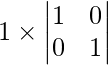Pregunta 1. Si A es una array singular, encuentre el valor de |A|.
Solución:
Dado que A es una array singular.
Entonces, como sabemos que si A es una array × n y es singular, el valor de su determinante siempre es 0.
Así, |A| = 0.
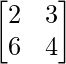
Pregunta 2. ¿Para qué valor de x, la siguiente array es singular?
Solución:
Dado que
Como sabemos, si A es una array × n y es singular, entonces, el valor de su determinante siempre es 0.
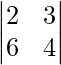
=> |A| = 0
=>
=> 4(5 – x) – 2(x + 1) = 0
=> 20 – 4x – 2x – 2 = 0
=> 18 – 6x = 0
=> 18 = 6x
=> x = 3
Por lo tanto, el valor de x es 3.
Pregunta 3. Encuentra el valor del determinante 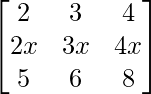 .
.
Solución:
Dado que
un =
|A| =
Entonces, al sacar x común de R 2 obtenemos,
|A| =
Como R 1 = R 2 , obtenemos
|A| = 0
Por lo tanto, el valor del determinante es 0.
Pregunta 4. Indique si la array 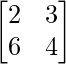 es singular o no singular.
es singular o no singular.
Solución:
Dado que
un =
|A| =
|A| = 2 (4) – 6 (3)
= 8 – 18
= -10
Como sabemos si A es una array ×n y es singular, entonces el valor de su determinante es siempre 0.
como |A| = -10 aquí, la array dada no es singular.
Pregunta 5. Encuentra el valor del determinante 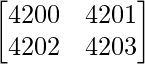 .
.
Solución:
Dado que
un =
|A| =
Al aplicar C 2 -> C 2 – C 1 , obtenemos
|A| =
|A| =
|A| = 4200 – 4202
|A| = -2
Por lo tanto, el valor del determinante es -2.
Pregunta 6. Encuentra el valor del determinante 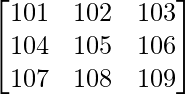 .
.
Solución:
Dado que
un =
|A| =
Al aplicar C 2 -> C 2 – C 1 y C 3 -> C 3 – C 1 , obtenemos
|A| =
|A| =
Al sacar 2 comunes de R 3 obtenemos,
|A| =
Como R 2 = R 3 , obtenemos
|A| = 0
Por lo tanto, el valor del determinante es cero.
Pregunta 7. Encuentra el valor del determinante 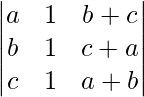 .
.
Solución:
Dado que
un =
|A| =
Al aplicar C 1 -> C 1 + C 3 obtenemos,
=
=
= (a + b + c) (0)
= 0
Por lo tanto, el valor del determinante es 0.
Pregunta 8. Si A = 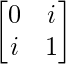 y B =
y B =  , encuentra el valor de |A| + |B|.
, encuentra el valor de |A| + |B|.
Solución:
Dado que
un =
|A| =
= 0 – yo 2
= – (-1)
= 1
Además, tenemos
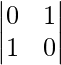
B =
|B| =
= 0 – 1
= -1
Asi que,
|A| + |B| = 1 + (-1)
= 1 – 1
= 0
Por lo tanto, el valor de |A| + |B| es 0
Pregunta 9. Si A = 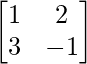 y B =
y B = 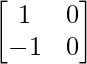 , encuentra |AB|.
, encuentra |AB|.
Solución:
Tenemos,
A =
y B =
Entonces, obtenemos
AB =
=
=
Ahora tenemos,
|AB| =
= -1 (0) – 0 (4)
= 0 – 0
= 0
Por lo tanto, el valor de |AB| es 0
Pregunta 10. Evaluar 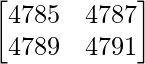 .
.
Solución:
Dado que
un =
|A| =
Al aplicar C 2 -> C 2 – C 1 obtenemos,
|A| =
=
Al sacar 2 comunes de R 2 obtenemos,
=
= 2 (4785 – 4789)
= 2 (-4)
= -8
Por lo tanto, el valor del determinante es 0.
Pregunta 11. Si w es una raíz cúbica imaginaria de la unidad, encuentre el valor de 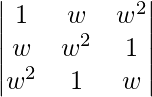 .
.
Solución:
Dado que,
un =
|A| =
Al aplicar C 1 -> C 1 + C _2 + C _3 obtenemos,
=
=
= 0
Pregunta 12. Si A = 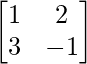 y B =
y B =  , encuentra |AB|.
, encuentra |AB|.
Solución:
Dado que
un =
|A| = -1 – 6
= -7
B =
|B| = – 2 + 12
= 10
Sabemos que si A y B son arrays cuadradas del mismo orden, entonces tenemos,
=> |AB| = |A|. |B|
= (-7) (10)
= -70
Por lo tanto, el valor de |AB| es -70.
Pregunta 13. Si A = [a ij ] es una array diagonal de 3 × 3 tal que a 11 = 1, a 22 = 2 a 33 = 3, entonces encuentre |A|.
Solución:
Dado que un 11 = 1, un 22 = 2 y un 33 = 3.
Si A es una array diagonal de orden nxn, entonces tenemos
=>
Entonces, obtenemos
|A| = 1 (2) (3)
= 6
Por lo tanto, el valor de |A| es 6
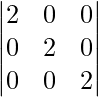
Pregunta 14. Si A = [a ij ] es una array escalar de 3 × 3 tal que a 11 = 2, entonces encuentre el valor de |A|.
Solución:
Dado que A = [a ij ] que es una array escalar de 3 × 3 y un 11 = 2,
Como sabemos, una array escalar es una array diagonal, en la que todos los elementos de la diagonal son iguales a un número escalar dado.
=> Un =
=
Al expandir a lo largo de C 1 , obtenemos
=
= 2 (2) (2)
= 8
Por lo tanto, el valor de |A| es 8
Pregunta 15. Si I 3 denota una array identidad de orden 3 × 3, encuentre el valor de su determinante.
Solución:
Como sabemos que en una array identidad, todos los elementos de la diagonal son 1 y los elementos restantes son 0.
Aquí,
yo 3 =
=
Al expandir a lo largo de C 1 , obtenemos
=
= 1
Por lo tanto, el valor del determinante es 1.
Pregunta 16. Una array A de orden 3 × 3 tiene determinante 5. ¿Cuál es el valor de |3A|?
Solución:
Dado que la array A es de orden 3 x 3 y el determinante = 5.
Si A es una array cuadrada de orden n y k es una constante, entonces tenemos
=> |kA| = k norte | A |
Aquí,
Número de filas = n
Además, k es un factor común de cada fila de k.
Por lo tanto, obtenemos
3A = 3 3 |A|
= 27 (5)
= 135
Por lo tanto, el valor de |3A| es 135
Pregunta 17. Al expandir por la primera fila, el valor del determinante de la array cuadrada de 3 × 3 A = [a ij ] es a 11 C 11 + a 12 C 12 + a 13 C 13 , donde [C ij ] es el cofactor de a ij en A. Escribe la expresión para su valor al expandir por la segunda columna.
Solución:
Como sabemos que si una array cuadrada (digamos A) es de orden n, entonces la suma de los productos de los elementos de una fila o una columna con sus cofactores es siempre igual a det (A).
Asi que,
También,
Al expandir a lo largo de R 1 obtenemos,
|A| = un 11 C 11 + un 12 C 12 + un 13 C 13
Ahora,
Al expandir a lo largo de C 2 obtenemos,
|A| = un 12 C 12 + un 22 C 22 + un 32 C 32
Pregunta 18. Al expandir por la primera fila, el valor del determinante de la array cuadrada de 3 × 3 A = [a ij ] es a 11 C 11 + a 12 C 12 + a 13 C 13 , donde [C ij ] es el cofactor de a ij en A. Escribe la expresión para su valor al expandir por la segunda columna.
Solución:
Como sabemos que si una array cuadrada (digamos A) es de orden n, entonces la suma de los productos de los elementos de una fila o una columna con sus cofactores es siempre igual a det (A).
Asi que,
También,
Al expandir a lo largo de R 1 obtenemos,
|A| = un 11 C 11 + un 12 C 12 + un 13 C 13
Ahora,
Al expandir a lo largo de C 2 obtenemos,
|A| = un 12 C 12 + un 22 C 22 + un 32 C 32 = 5
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA