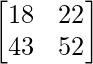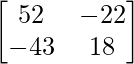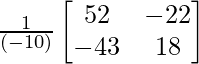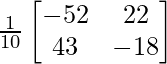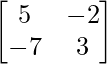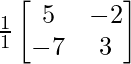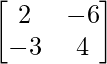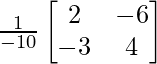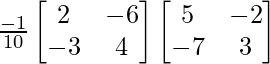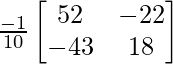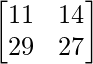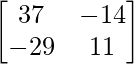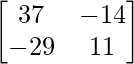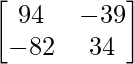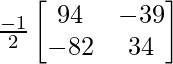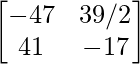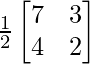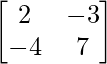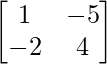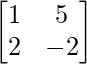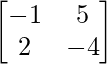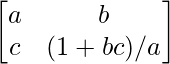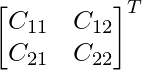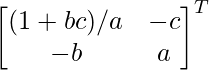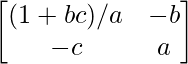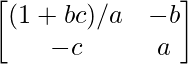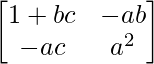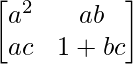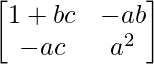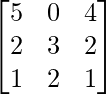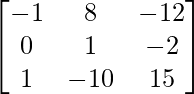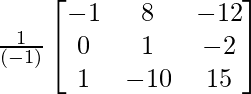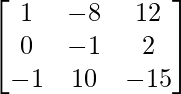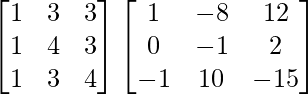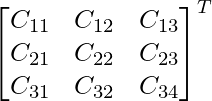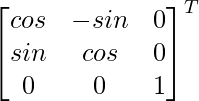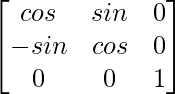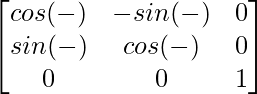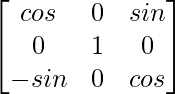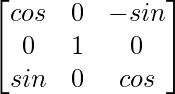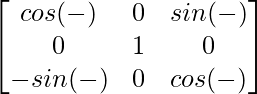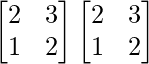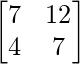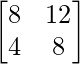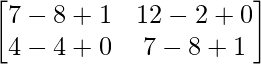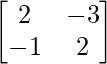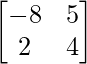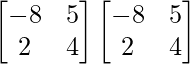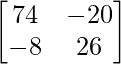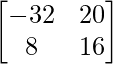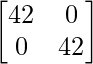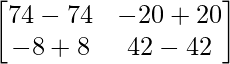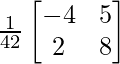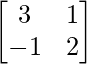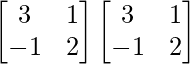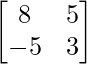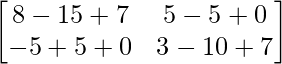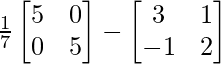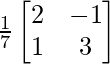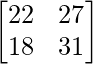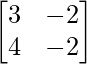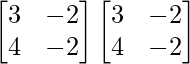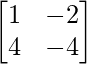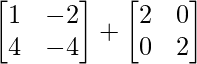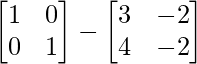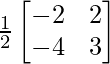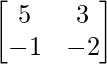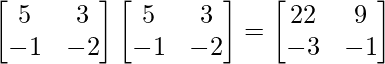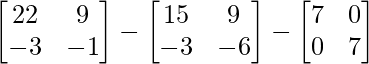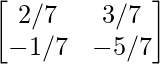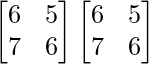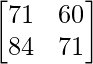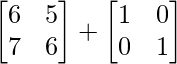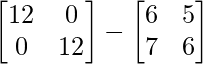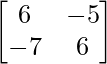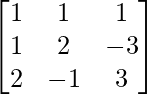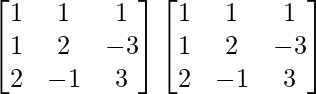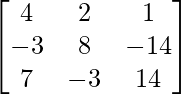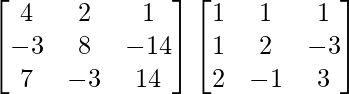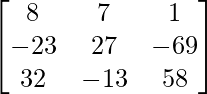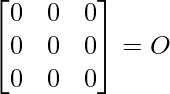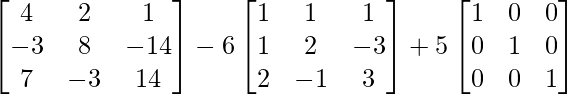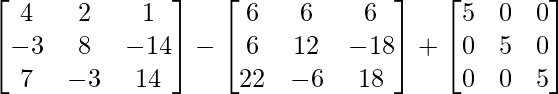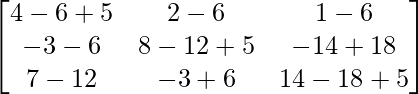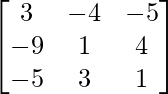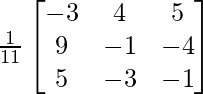Pregunta 10. Para las siguientes partes de arrays verificar que (AB) -1 = B -1 A -1 .
(i) A = 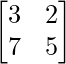 y B =
y B = 
Solución:
Demostrar (AB) -1 = B -1 A -1
Tomamos LHS
AB =
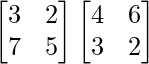
=
|AB| = 18 × 52 – 22 × 43
= 936 – 946 = -10
adj(AB) =
AB – 1 = adj(AB)/|AB| =
=
Ahora,
un =
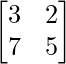
|A| = 15 – 14 = 1
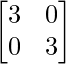
adj A =
Por lo tanto, A -1 = adj A/|A| =
B =

|B| = 8 – 18 = -10
adj B =
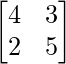
Por lo tanto, B -1 = adj B/|B| =
Ahora, tomamos RHS
B – 1 A – 1 =
=
=
LHS = RHS
Por lo tanto, demostrado
(ii) A = 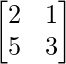 y B =
y B = 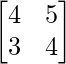
Solución:
Demostrar (AB) -1 = B -1 A -1
Tomamos LHS
AB =
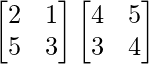
=
|AB| = 11 × 27 – 29 × 14
= 407 – 406 = 1
adj(AB) =
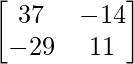
AB – 1 = adj(AB)/|AB| =
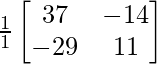
=
Ahora,
un =
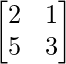
|A| = 6 – 5 = 1
adj A=
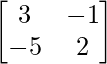
Por lo tanto, A -1 = adj A/|A| =
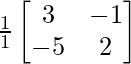
B =
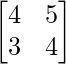
|B| = 16 – 15 = 1
adj B =
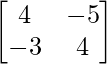
Por lo tanto, B -1 = adj B/|B| =
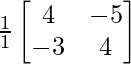
Ahora, tomamos RHS
B – 1 A – 1 =
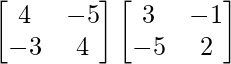
=
LHS = RHS
Por lo tanto, demostrado
Pregunta 11. Sean A = 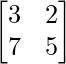 y B =
y B = 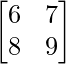 . Encuentre (AB) -1 .
. Encuentre (AB) -1 .
Solución:
AB =
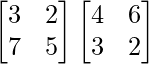
=
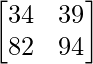
|AB| = 34 × 94 – 39 × 82 = -2
adj(AB) =
AB – 1 = adj(AB)/|AB| =
=
Pregunta 12. Dado A = 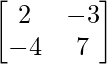 , Calcule A -1 y demuestre que 2A -1 = 9I – A.
, Calcule A -1 y demuestre que 2A -1 = 9I – A.
Solución:
un =
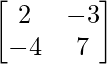
|A| = 14 – 12 = 2
adj A =
Por lo tanto, A -1 = adj A/|A| =
Para mostrar 2A -1 = 9I – A.
IZQ = 2 × (1/2)
=
Ahora tomamos RHS
= 9I – A
=
–
=
LHS = RHS
Por lo tanto probado
Pregunta 13. Si A =  , entonces demuestre que A – 3I = 2(I + 3A -1 ).
, entonces demuestre que A – 3I = 2(I + 3A -1 ).
Solución:
Aquí, A =
|A| = 4 – 10 = -6
adj A =
Por lo tanto, A -1 = adj A/|A| =
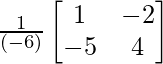
Para mostrar, A – 3I = 2(I + 3A -1 )
Ahora tomamos LHS
= A – 3I
=
– 3
=
Ahora tomamos RHS
= 2I + 6A -1
= 2
+ 6 × (1/6)
=
LHS = RHS
Por lo tanto probado
Pregunta 14. Encuentre la inversa de la array A = 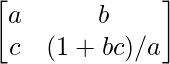 y demuestre que aA -1 = (a 2 + bc + 1)I – aA.
y demuestre que aA -1 = (a 2 + bc + 1)I – aA.
Solución:
Aquí, A =
|A| = (a + abc)/a – bc = 1
Por lo tanto, existe el inverso de A
Cofactor de A son,
C 11 = (1 + bc)/a C 12 = -c
C 21 = -b C 22 = un
adj A =
=
=
A – 1 = 1/|A|. adj.
= 1/1
=
Para mostrar que
aA -1 = (a 2 + bc + 1)I – aA.
LHS = aA -1
= un
=
RHS = (a 2 + bc + 1)I – aA
=
– un
=
–
=
LHS = RHS
Por lo tanto probado
Pregunta 15. Dado A = 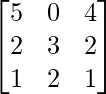 , B -1 =
, B -1 = 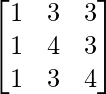 , Calcular (AB) -1 .
, Calcular (AB) -1 .
Solución:
Sabemos (AB) -1 = B -1 A -1
Aquí, A =
|A| = 5(3 – 4) + 4(4 – 3) = -5 + 4 = -1
Los cofactores de A son:
C 11 = -1 C 12 = 0 C 13 = 1
C 21 = 8 C 22 = 1 C 23 = -10
C 31 = -12 C 32 = -2 C 33 = 15
adj A =
A – 1 = 1/|A|. adj.
Por lo tanto, A – 1 =
=
(AB) -1 = B -1 A -1
=
=
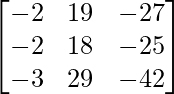
Pregunta 16. Sean F(α) = 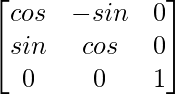 y G(β) =
y G(β) = 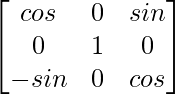 , Demuestra que
, Demuestra que
(i) [F(α)] -1 = F(-α)
Solución:
Tenemos F(a) =
|F(a)| = cos 2 α + sen 2 α = 1
Por lo tanto, existe el inverso de F(α)
Los cofactores de F(α) son:
C 11 = cosα C 12 = -sinα C 13 = 0
C 21 = senα C 22 = cosα C 23 = 0
C 31 = 0 C 32 = 0 C 33 = 1
Ajuste F(α) =
=
=
[F(α)] -1 = 1/|F(α)|. adj F(α)
Por tanto, [F(α)] -1 = 1/1
=
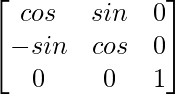
Ahora, F(-α) =
=
Entonces, [F(α)] -1 = F(-α)
Por lo tanto, demostrado
(ii) [G(β)] -1 = G(-β)
Solución:
Tenemos G(β) =
|G(β)| = cos 2 β + sen 2 β = 1
Por lo tanto, existe el inverso de G(β)
Los cofactores de G(β) son:
C 11 = cosβ C 12 = 0 C 13 = senβ
C 21 = 0 C 22 = 1 C 23 = 0
C 31 = -senβ C 32 = 0 C 33 = senβ
Adj G(β) =
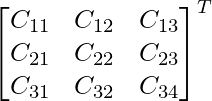
=
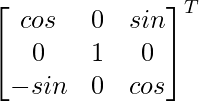
=
[G(β)] -1 = 1/|G(β)|. adj G(β)
Por lo tanto, [G(β)] -1 = 1/1
=
Ahora, G(-β) =
=
Entonces, [G(β)] -1 = G(-β)
Por lo tanto, demostrado
(iii) [F(α)G(β)] -1 = F(-α)G(-β)
Solución:
Ya sabemos que S[G(β)] -1 = G(-β)
[F(α)] -1 = F(-α)
Tomando LHS = [F(α)G(β)] -1
= [F(α)] -1 [G(β)] -1
= F(-α)G(-β) = lado derecho
Por lo tanto, demostrado
Pregunta 17. Si A =  , Verifique que A 2 – 4A + I = O, donde I =
, Verifique que A 2 – 4A + I = O, donde I =  y O =
y O =  , Por lo tanto, encuentre A -1 .
, Por lo tanto, encuentre A -1 .
Solución:
Aquí, A =
un 2 =
=
4A = 4
=
A 2 – 4A + I = O
=
–
+
=
Por lo tanto, =
Ahora, A 2 – 4A + I = O
A 2 – 4A = -I
Multiplicando ambos lados por A -1 ambos lados obtenemos
AA(A -1 ) – 4AA -1 = -IA -1
IA – 4I = -A -1
A -1 = 4I – IA
=
–

=
Pregunta 18. Muestre que A = 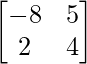 satisface la ecuación A 2 + 4A – 42I = O. Por lo tanto, encuentre A -1 .
satisface la ecuación A 2 + 4A – 42I = O. Por lo tanto, encuentre A -1 .
Solución:
Aquí, A =
un 2 =
=
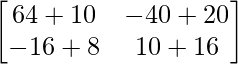
=
4A = 4
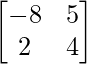
=
A 2 + 4A – 42I =
+
–
=
Por eso,
Ahora, A 2 + 4A – 42I = 0
⇒ A -1 A.A + 4A -1 .A – 42A -1 I = 0
⇒ IA + 4I – 42A -1 = 0
⇒ A -1 = 1/42 [A + 4I]
⇒ A -1 =
Pregunta 19. Si A = 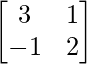 , demuestre que A 2 – 5A + 7I = O. Por lo tanto, encuentre A -1 .
, demuestre que A 2 – 5A + 7I = O. Por lo tanto, encuentre A -1 .
Solución:
Aquí, A =
un 2 =
=
Ahora, A 2 – 5A + 7I =
+ 5
+ 7
=
=
Ahora, A 2 – 5A + 7I = O
Multiplicando por A -1 en ambos lados
⇒ A -1 AA + 5AA – 1 + 7IA -1 = 0
⇒ A -1 = 1/7[5I – A]
⇒ A -1 =
⇒ A -1 =
Pregunta 20. Si A = 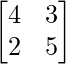 , encuentre x e y tales que A 2 – xA + yI = O. Por lo tanto, evalúe A -1 .
, encuentre x e y tales que A 2 – xA + yI = O. Por lo tanto, evalúe A -1 .
Solución:
Aquí, A =
un 2 =
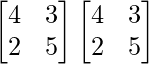
=
Ahora, A 2 – xA + yI = O
⇒
–
+
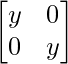
=
⇒ 22 – 4x + y = 0
⇒ 4x – y = 22 ………(yo)
o
18 – 2x = 0
⇒ x = 9
Poniendo x = 9 en la ecuación (i)
⇒ y = 14
A 2 – 9A + 14I = 0
⇒ 9A = A 2 + 14I
⇒ 9A -1 A = A -1AA + 14A -1
⇒ 9I = IA + 14A -1
⇒ A -1 = 1/14[9I – A] = 1/14(
)
⇒ A -1 =
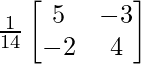
Pregunta 21. Si A = 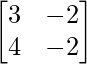 , encuentra el valor de λ tal que A 2 = λA – 2I. Por lo tanto, encuentre A -1 .
, encuentra el valor de λ tal que A 2 = λA – 2I. Por lo tanto, encuentre A -1 .
Solución:
Aquí, A =
un 2 =
=
Si A 2 = λA – 2I
λA = A2 + 2I
⇒ λ
=
⇒ λ
=
⇒ λ = 1
Ahora, A 2 = λA – 2I
Multiplicando ambos lados A -1
⇒ A -1 AA = A -1 A – 2A -1 I
⇒ A = Yo – 2A -1
⇒ 2A -1 = I – A =
A – 1 =
Pregunta 22. Muestre que A = 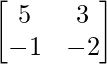 satisface la ecuación x 2 – 3x – 7 = 0. Por lo tanto, encuentre A -1 .
satisface la ecuación x 2 – 3x – 7 = 0. Por lo tanto, encuentre A -1 .
Solución:
Aquí, A =
un 2 =
Ahora, A 2 – 3A – 7=
=
Tenemos, A 2 – 3A – 7 = 0
⇒ A -1 AA – 3A -1 A – 7A -1 = 0
⇒ A-3I – 7A -1 = 0
⇒ 7A -1 = A – 3I
⇒ 7A -1 =
–
A – 1 =
Pregunta 23. Muestre que A =  satisface la ecuación x 2 – 12x + 1 = 0. Por lo tanto, encuentre A -1 .
satisface la ecuación x 2 – 12x + 1 = 0. Por lo tanto, encuentre A -1 .
Solución:
Aquí, A =
un 2 =
=
Ahora, A 2 – 12A + I =
–
=
Tenemos, A 2 – 12A + I = 0
⇒ A – 12I + A -1 = 0
⇒ A -1 = 12I – A
⇒ A -1 =
⇒ A -1 =
Pregunta 24. Para la array A = 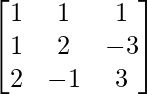 muestre que A 3 – 6A 2 + 5A + 11I 3 = O. Por lo tanto, encuentre A -1 .
muestre que A 3 – 6A 2 + 5A + 11I 3 = O. Por lo tanto, encuentre A -1 .
Solución:
Aquí, A =
un 2 =
=
un 3 =
=
A 3 – 6A 2 + 5A + 11I
=
– 6
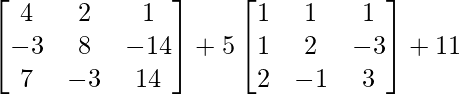
=
=
=
Tenemos, A 3 – 6A 2 + 5A + 11I = O.
⇒ A -1 (AAA) – 6A -1 (AA) + 5A -1 A + 11IA -1 = 0
⇒ A 2 – 6A + 5I = -11A -1
⇒ -11A -1 = (A 2 – 6A + 5I)
=
=
=
=
Por lo tanto, A – 1 =
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA