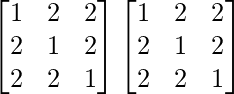
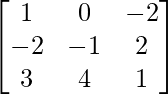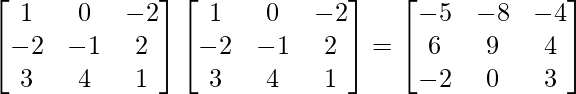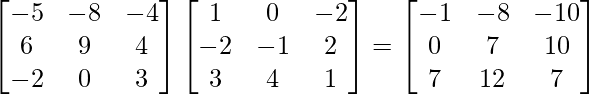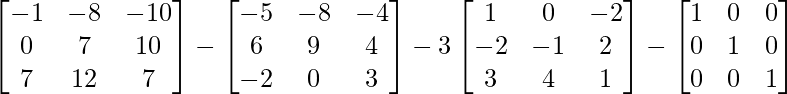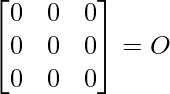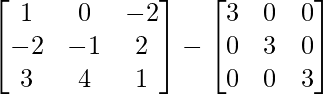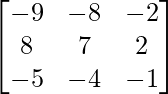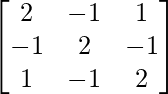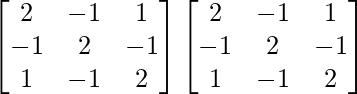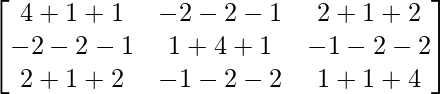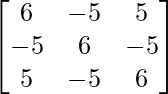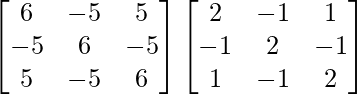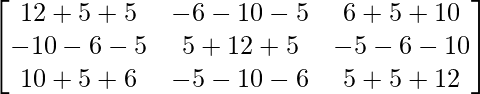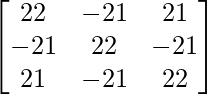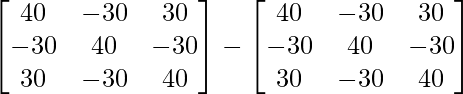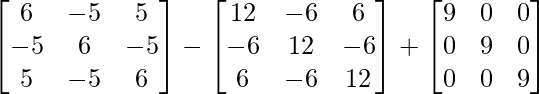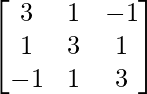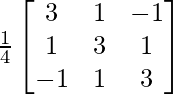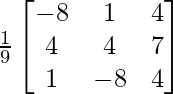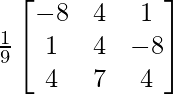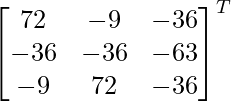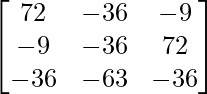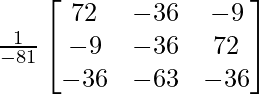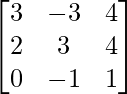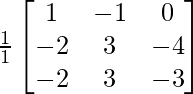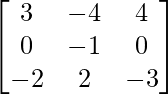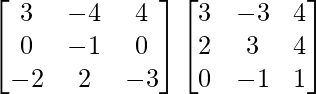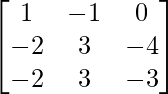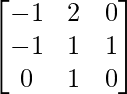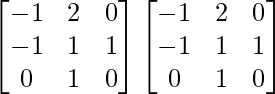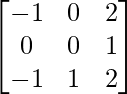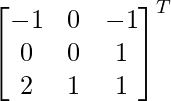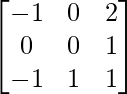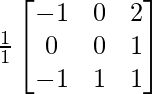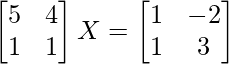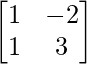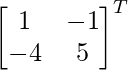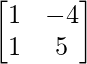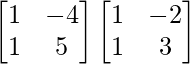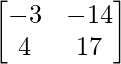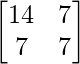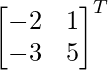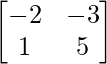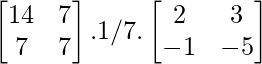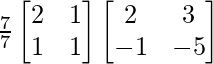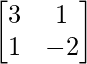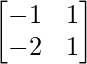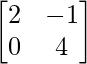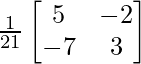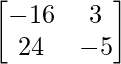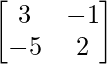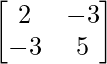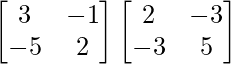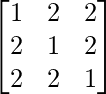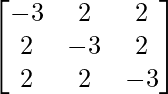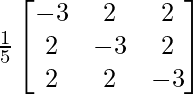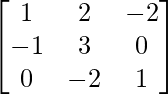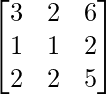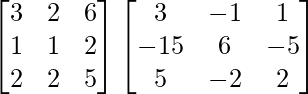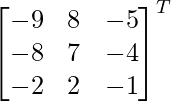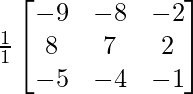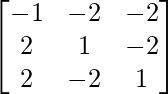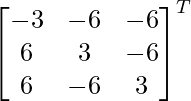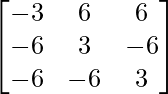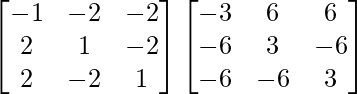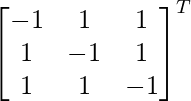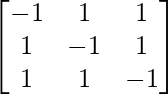Pregunta 25. Muestre que la array A = 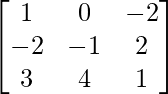 satisface la ecuación A 3 – A 2 – 3A – I 3 = 0. Por lo tanto, encuentre A -1 .
satisface la ecuación A 3 – A 2 – 3A – I 3 = 0. Por lo tanto, encuentre A -1 .
Solución:
Aquí, A =
un 2 =
un 3 =
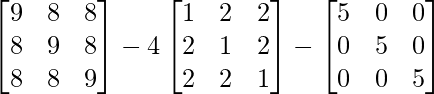
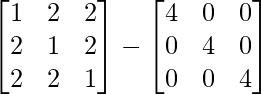
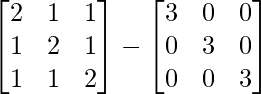
Ahora A 3 – A 2 – 3A – I 3 =
=
=
Entonces, A 3 – A 2 – 3A – I 3 = 0
⇒ A -1 (AAA) – A -1 (AA) – 3A -1 A – A -1 I = 0
⇒ A 2 – A – 3I – A -1 = 0
⇒ A -1 = A 2 – A – 3I
=
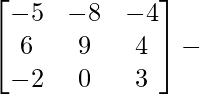
Por lo tanto, A – 1 =
Pregunta 26. Si A = 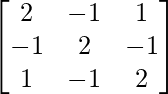 . Verifique que A 3 – 6A 2 + 9A – 4I = O y, por lo tanto, encuentre A -1 .
. Verifique que A 3 – 6A 2 + 9A – 4I = O y, por lo tanto, encuentre A -1 .
Solución:
Aquí, A =
un 2 =
=
=
UN 3 = UN 2 UN =
=
=
Ahora, A 3 – 6A 2 + 9A – 4I
=
=
=
=
Entonces, A 3 – 6A 2 + 9A – 4I = O
Multiplicando ambos lados por A -1
⇒ A -1 (AAA) – 6A -1 (AA) 9A -1 A – 4A -1 I = O
⇒ IAA – 6AI + 9I = 4A -1
⇒ 4A -1 = A 2 I – 6AI + 9I
=
=
=
⇒ A -1 =
Pregunta 27. Si A = 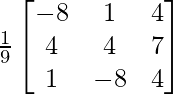 , demuestre que A -1 = A T .
, demuestre que A -1 = A T .
Solución:
Aquí, A =
UN T =
Ahora, encontrando A -1
|A| = 1/9[-8(16 + 56) – 1(16 – 7) + 4(-32 – 4)]
= -81
Por lo tanto, existe el inverso de A
Los cofactores de A son:
C 11 = 72 C 12 = -9 C 13 = -36
C 21 = -36 C 22 = -36 C 23 = -63
C 31 = -9 C 32 = 72 C 33 = -36
adj A =
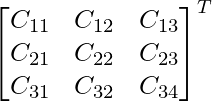
=
=
A – 1 = 1/|A|. adj.
Por lo tanto, A – 1 =
=

= UNA T
Por lo tanto probado
Pregunta 28. Si A = 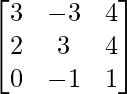 , demuestre que A -1 = A 3 .
, demuestre que A -1 = A 3 .
Solución:
Aquí, A =
|A| = 3(-3 + 4) + 3(2 – 0) + 4(-2 – 0)
= 3 + 6 – 8
= 1
Por lo tanto, existe el inverso de A
Los cofactores de A son:
C 11 = 1 C 12 = -2 C 13 = -2
C 21 = -1 C 22 = 3 C 23 = 3
C 31 = 0 C 32 = -4 C 33 = -3
adj A =
A – 1 = 1/|A|. adj.
=
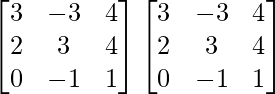
Ahora, A 2 =
=
un 3 =
=
= A- 1
Por lo tanto probado
Pregunta 29. Si A = 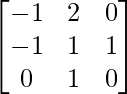 , demuestre que A 2 = A -1 .
, demuestre que A 2 = A -1 .
Solución:
Aquí, A =
IZQ = A 2
=
=
|A| = -1(1 – 0) – 2(-1 – 0) + 0
= 1
Por lo tanto, existe el inverso de A
Los cofactores de A son:
C 11 = -1 C 12 = 0 C 13 = -1
C 21 = 0 C 22 = 0 C 23 = 1
C 31 = 21 C 32 = 1 C 33 = 1
adj A =
=
A – 1 = 1/|A|. adj.
Por lo tanto, A – 1 =
=
= un 2
Por lo tanto probado
Pregunta 30. Resuelve la ecuación matricial 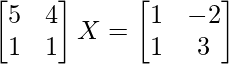 , donde X es una array de 2×2.
, donde X es una array de 2×2.
Solución:
Tenemos,
Sean A =
y B =
Asi que. AX = B
⇒ X = A -1 B
Ahora, |A| = 5 – 4 = 1
Los cofactores de A son:
C 11 = 1 C 12 = -1
C 21 = -4 C 22 = 5
adj A =
=
A – 1 =
Por lo tanto, X =
X =
Pregunta 31. Encuentra la array X que satisface la ecuación matricial: X 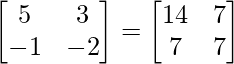 .
.
Solución:
Tenemos,
Sean A =
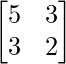
y B =
Entonces, XA = B
XAA – 1 = BA- 1
XI = BA- 1 ………..(i)
Ahora, |A| = -7
Los cofactores de A son:
C 11 = -2 C 12 = 1
C 21 = -3 C 22 = 5
adj A =
=
A -1 = 1/|A|.adj (A)
=
Por lo tanto, X =
=
X =
Pregunta 32. Encuentra la array X para la cual: 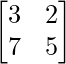 X
X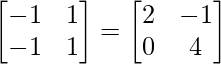
Solución:
Sea, A =
B =
C =
Entonces la ecuación dada se convierte en
UN × B = C
⇒ X = A -1 CB -1
Ahora |A| = 35 -14 = 21
|B| = -1 + 2 = 1
A -1 = ajuste (A)/|A| =
B -1 = ajuste (B)/|A| =
X = A -1 CB -1 =
=
Pregunta 33. Encuentra la array X que satisface la ecuación: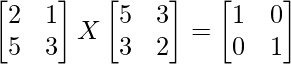
Solución:
Sea A =
B =
AXB = yo
X = A -1 B -1
|A| = 6 – 5 = 1
|B| = 10 – 9 = 1
A -1 = adj A /|A| =
B -1 = adj B/|B| =
X =
=
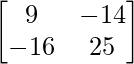
Pregunta 34. Si A = 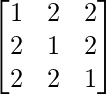 , Halla A -1 y prueba que A 2 – 4A – 5I = O.
, Halla A -1 y prueba que A 2 – 4A – 5I = O.
Solución:
Aquí, A =
un 2 =
=
Ahora, A 2 + 4A – 5I
=
=
Ahora, A 2 – 4A – 5I = O
⇒ A -1 AA – 4A -1 A – 5A -1 I = O
⇒ 5A -1 = [A – 4I]
=
=
A – 1 =
Pregunta 35. Si A es una array cuadrada de orden n, demuestre que |A adj A| = |A| norte _
Solución:
Dado, |A adj A| = |A| norte
Tomando LHS = |A Adj A|
= |A| |Adj A|
= |A| |A| n-1
= |A| n-1+1
= |A| n = lado derecho
Por lo tanto probado
Pregunta 36. Si A -1 = 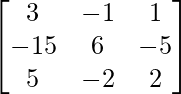 y B =
y B = 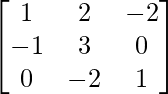 , encuentra (AB) -1 .
, encuentra (AB) -1 .
Solución:
Aquí, B =
|B| = 1(3 – 0) – 2(-1 – 0) – 2(2 – 0)
= 3 + 2 – 4 = 1
Por lo tanto, existe el inverso de B
Los cofactores de B son:
C 11 = 3 C 12 = 1 C 13 = 2
C 21 = 2 C 22 = 1 C 23 = 2
C 31 = 6 C 32 = 2 C 33 = 5
adj A =
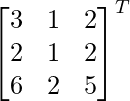
=
Por lo tanto,
B – 1 =
Por lo tanto, (AB) -1 = B -1 A -1
=
=
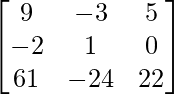
Pregunta 37. Si A = 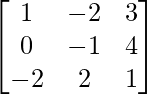 , encuentre (A T ) -1 .
, encuentre (A T ) -1 .
Solución:
Suponiendo que B = A T =
|B| = 1(-1 – 8) – 0 – 2(-8 + 3)
= -9 + 10 = 1
Por lo tanto, existe el inverso de B
Los cofactores de B son:
C 11 = -9 C 12 = 8 C 13 = -5
C 21 = -8 C 22 = 7 C 23 = -4
C 31 = -2 C 32 = 2 C 33 = -1
adj B =
=
B – 1 =
o (A T ) -1 =
Pregunta 38. Encuentre el adjunto de la array A = 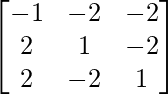 y, por lo tanto, demuestre que A (adj A) = |A|I 3 .
y, por lo tanto, demuestre que A (adj A) = |A|I 3 .
Solución:
Aquí, A =
|A| = -1(1 – 4) – 2(2 + 4) – 2(-4 – 2)
= 3 + 12 + 12 = 27
Por lo tanto, existe el inverso de A
Los cofactores de A son:
C 11 = -3 C 12 = -6 C 13 = -6
C 21 = 6 C 22 = 3 C 23 = -6
C 31 = 6 C 32 = -6 C 33 = 3
adj A =
=
A (adj. A) =
=
o A (adj. A) = 27
Por lo tanto, A (adj A) = |A|I 3
Por lo tanto probado
Pregunta 39. Si A = 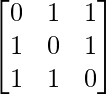 , A -1 y demuestra que A -1 = 1/2(A 2 – 3I).
, A -1 y demuestra que A -1 = 1/2(A 2 – 3I).
Solución:
Aquí, A =
|A| = 0 – 1(0 – 1) + 1(1 – 0)
= 1 + 1 = 2
Por lo tanto, existe el inverso de A
Los cofactores de A son:
C 11 = -1 C 12 = 1 C 13 = 1
C 21 = 1 C 22 = -1 C 23 = 1
C 31 = 1 C 32 = 1 C 33 = -1
adj A =
=
A – 1 = 1/|A|. adj.
Por lo tanto, A – 1 =
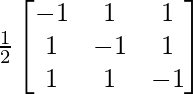
Ahora, A 2 – 3I =

=
=
Por lo tanto, A -1 = 1/2(A 2 – 3I)
Por lo tanto probado
Publicación traducida automáticamente
Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA