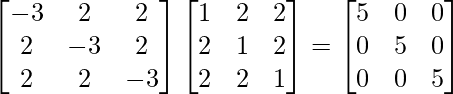
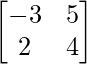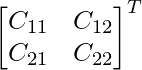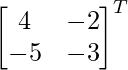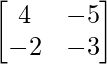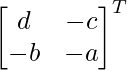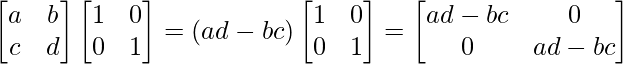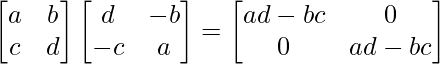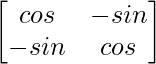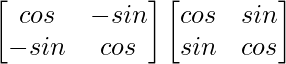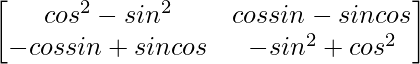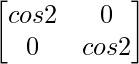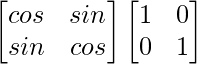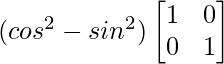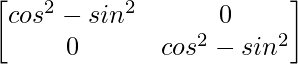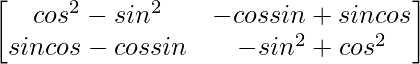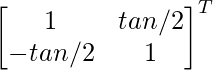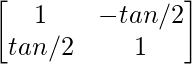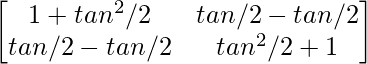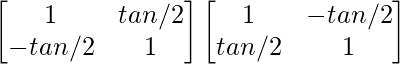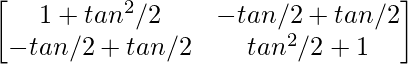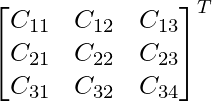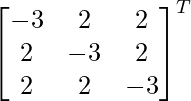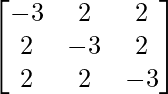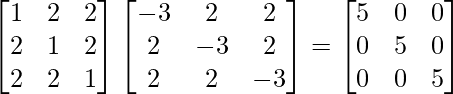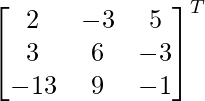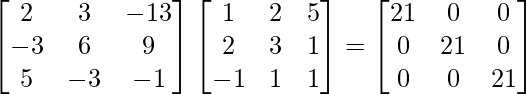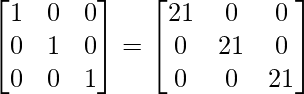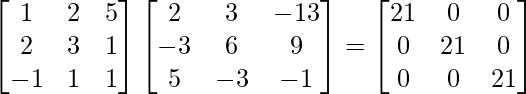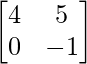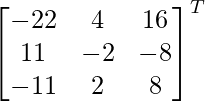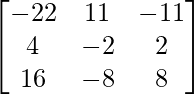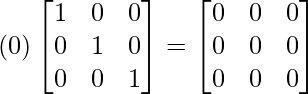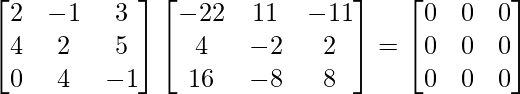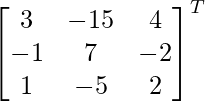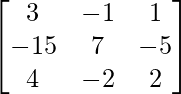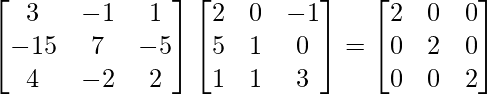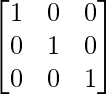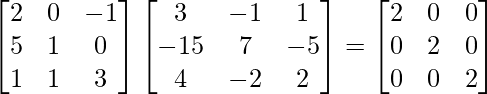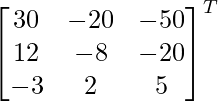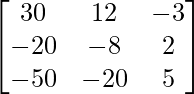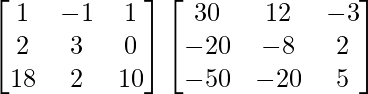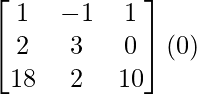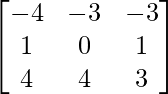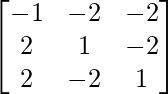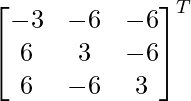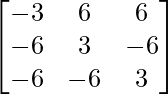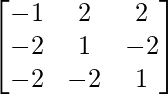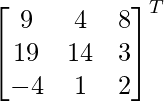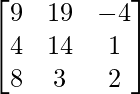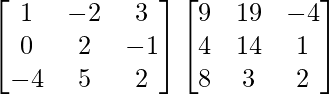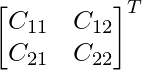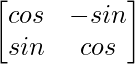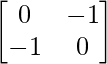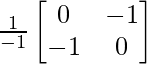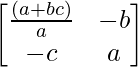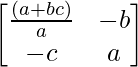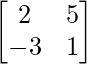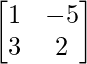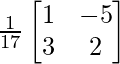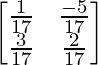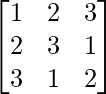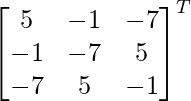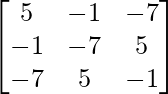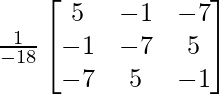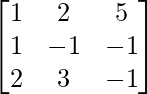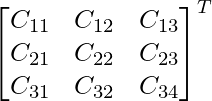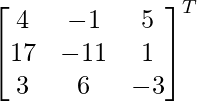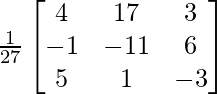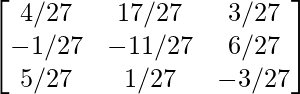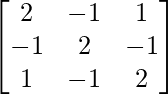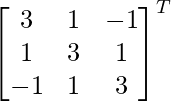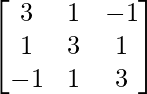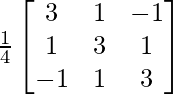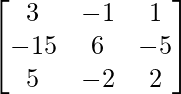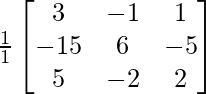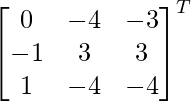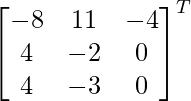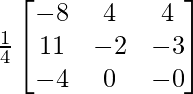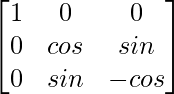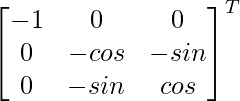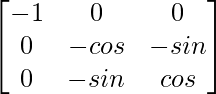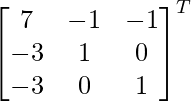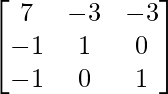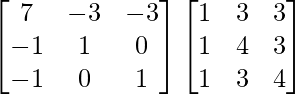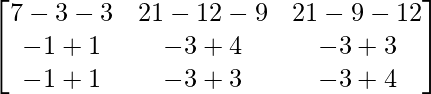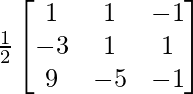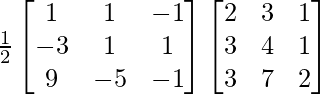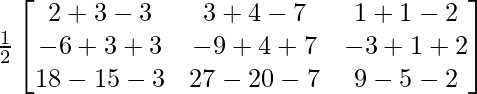Clase 12 Soluciones RD Sharma – Capítulo 7 Adjuntas e inversas de una array – Ejercicio 7.1 | Serie 1

Posted on by Rudeus Greyrat

Pregunta 1. Encuentra el adjunto de las siguientes arrays:

Verifique que (adj A)A = |A|I = A(adj A) para las arrays anteriores:

(i) 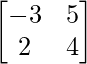\begin{bmatrix}-3&5\\2&4\end{bmatrix}  

Solución:

Aquí, A = \begin{bmatrix}-3&5\\2&4\end{bmatrix}

Los cofactores de A son:

C 11 = 4 C 12 = -2

C 21 = -5 C 22 = -3

adj A = \begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}^T

(adj A) = \begin{bmatrix}4&-2\\-5&-3\end{bmatrix}^T

= \begin{bmatrix}4&-5\\-2&-3\end{bmatrix}

Para probar, (adj A)A = |A|I = A(adj A)

(adj. A)A = \begin{bmatrix}4&-5\\-2&-3\end{bmatrix}\begin{bmatrix}-3&5\\2&4\end{bmatrix}=\begin{bmatrix}-22&0\\0&-22\end{bmatrix}  

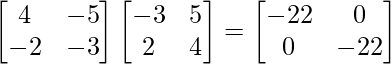
|A|Yo =  \begin{bmatrix}-3&5\\2&4\end{bmatrix}\begin{bmatrix}1&0\\0&1\end{bmatrix} =(-22)\begin{bmatrix}1&0\\0&1\end{bmatrix}  = \begin{bmatrix}-22&0\\0&-22\end{bmatrix}  

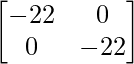
A(adj. A) = \begin{bmatrix}-3&5\\2&4\end{bmatrix}\begin{bmatrix}4&-5\\-2&-3\end{bmatrix}=\begin{bmatrix}-22&0\\0&-22\end{bmatrix}

Por lo tanto, (adj A)A = |A|I = A(adj A)

Por lo tanto probado

(ii) 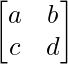\begin{bmatrix}a&b\\c&d\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}a&b\\c&d\end{bmatrix}

Los cofactores de A son:

C 11 = re C 12 = -c

C 21 = -b C 22 = un

(adj A) = \begin{bmatrix}d&-c\\-b&-a\end{bmatrix}^T

= \begin{bmatrix}d&-b\\-c&a\end{bmatrix}

Para probar, (adj A)A = |A|I = A(adj A)

(adj. A)A = \begin{bmatrix}d&-b\\-c&a\end{bmatrix}\begin{bmatrix}a&b\\c&d\end{bmatrix}=\begin{bmatrix}ad-bc&bd-bd\\-ac+ac&-bc+ad\end{bmatrix}=\begin{bmatrix}ad-bc&0\\0&ad-bc\end{bmatrix}

|A|I =\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}1&0\\0&1\end{bmatrix} =(ad-bc)\begin{bmatrix}1&0\\0&1\end{bmatrix} =\begin{bmatrix}ad-bc&0\\0&ad-bc\end{bmatrix}

A(adj. A) =\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}d&-b\\-c&a\end{bmatrix}=\begin{bmatrix}ad-bc&0\\0&ad-bc\end{bmatrix}

Por lo tanto, (adj A)A = |A|I = A(adj A)

Por lo tanto probado

(iii) 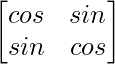\begin{bmatrix}cos α&sin α\\sin α&cosα\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}cos α&sin α\\sin α&cosα\end{bmatrix}

Los cofactores de A son:

C 11 = cos α C 12 = -sen α

C 21 = -sen α C 22 = cos α

(adj A) =\begin{bmatrix}cos α&-sin α\\-sin α&cosα\end{bmatrix}^T

=\begin{bmatrix}cos α&-sin α\\-sin α&cosα\end{bmatrix}

Para probar, (adj A)A = |A|I = A(adj A)

(adj. A)A = \begin{bmatrix}cos α&-sin α\\-sin α&cosα\end{bmatrix}\begin{bmatrix}cos α&sin α\\sin α&cosα\end{bmatrix}

=\begin{bmatrix}cos^2α-sin^2α&cosαsinα-sinαcosα\\-cosαsinα+sinαcosα&-sin^2α+cos^2α\end{bmatrix}

=\begin{bmatrix}cos 2α&0\\0&cos2α\end{bmatrix}

|A|I = \begin{bmatrix}cos α&sin α\\sin α&cosα\end{bmatrix}\begin{bmatrix}1&0\\0&1\end{bmatrix}

=(cos^2α-sin^2α)\begin{bmatrix}1&0\\0&1\end{bmatrix}

=\begin{bmatrix}cos^2α-sin^2α&0\\0&cos^2α-sin^2α\end{bmatrix}

=\begin{bmatrix}cos2α&0\\0&cos2α\end{bmatrix}

A(adj. A) = \begin{bmatrix}cos α&sin α\\sin α&cosα\end{bmatrix}\begin{bmatrix}cos α&-sin α\\-sin α&cosα\end{bmatrix}

=\begin{bmatrix}cos^2α-sin^2α&-cosαsinα+sinαcosα\\sinαcosα-cosαsinα&-sin^2α+cos^2α\end{bmatrix}

=\begin{bmatrix}cos 2α&0\\0&cos2α\end{bmatrix}

Por lo tanto, (adj A)A = |A|I = A(adj A) 

Por lo tanto probado

(iv) 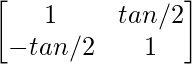\begin{bmatrix}1&tan α/2\\-tan α/2&1\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}1&tan α/2\\-tan α/2&1\end{bmatrix}

Los cofactores de A son:

C 11 = 1 C 12 = -(-tan α/2) = tan α/2

C 21 = -tan α/2 C 22 = 1

adj A = \begin{bmatrix}1&tan α/2\\-tan α/2&1\end{bmatrix}^T

=\begin{bmatrix}1&-tan α/2\\tan α/2&1\end{bmatrix}

Para probar, (adj A)A = |A|I = A(adj A)

|A| = \begin{bmatrix}1&tan α/2\\-tan α/2&1\end{bmatrix}

= 1 + tan 2 α/2

= segundo 2 α/2

(adj)A = \begin{bmatrix}1&-tan α/2\\tan α/2&1\end{bmatrix}\begin{bmatrix}1&tan α/2\\-tan α/2&1\end{bmatrix}

=\begin{bmatrix}1+tan^2 α/2&tan α/2-tan α/2\\tan α/2-tan α/2&tan^2 α/2+1\end{bmatrix}

=\begin{bmatrix}sec^2 α/2&0\\0&sec^2 α/2\end{bmatrix}

|A|I = (seg 2 α/2)\begin{bmatrix}1&0\\0&1\end{bmatrix}

=\begin{bmatrix}sec^2 α/2&0\\0&sec^2 α/2\end{bmatrix}

A(adj. A) = \begin{bmatrix}1&tan α/2\\-tan α/2&1\end{bmatrix}\begin{bmatrix}1&-tan α/2\\tan α/2&1\end{bmatrix}

=\begin{bmatrix}1+tan^2 α/2&-tan α/2+tan α/2\\-tan α/2+tan α/2&tan^2 α/2+1\end{bmatrix}

=\begin{bmatrix}sec^2 α/2&0\\0&sec^2 α/2\end{bmatrix}

Por lo tanto, (adj A)A = |A|I = A(adj A) 

Por lo tanto probado

Pregunta 2. Calcule el adjunto de cada una de las siguientes arrays:

Verifique que (adj A)A = |A|I = A(adj A) para las arrays anteriores:

(i) 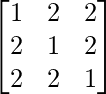\begin{bmatrix}1&2&2\\2&1&2\\2&2&1\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}1&2&2\\2&1&2\\2&2&1\end{bmatrix}

Los cofactores de A son

C 11 =  \begin{bmatrix}1&2\\2&1\end{bmatrix}  = -3

C 21 =  \begin{bmatrix}2&2\\2&1\end{bmatrix}  = 2

C 31 =  \begin{bmatrix}2&2\\1&2\end{bmatrix}  = 2

C 12 =  \begin{bmatrix}2&2\\2&1\end{bmatrix}  = 2

C 22 =  \begin{bmatrix}1&2\\2&1\end{bmatrix} =-3

C 32 =  \begin{bmatrix}1&2\\2&2\end{bmatrix}  = 2

C 13 =  \begin{bmatrix}2&1\\2&2\end{bmatrix}  = 2

C 23 =  \begin{bmatrix}1&2\\2&2\end{bmatrix}  = 2

C 33 =  \begin{bmatrix}1&2\\2&1\end{bmatrix}  = -3

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

=\begin{bmatrix}-3&2&2\\2&-3&2\\2&2&-3\end{bmatrix}^T

=\begin{bmatrix}-3&2&2\\2&-3&2\\2&2&-3\end{bmatrix}

Para probar, (adj A)A = |A|I = A(adj A)

|A| = -3 + 4 + 4 = 5

(adj. A)A = \begin{bmatrix}-3&2&2\\2&-3&2\\2&2&-3\end{bmatrix}\begin{bmatrix}1&2&2\\2&1&2\\2&2&1\end{bmatrix}=\begin{bmatrix}5&0&0\\0&5&0\\0&0&5\end{bmatrix}

|A|I= (5) \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}  = \begin{bmatrix}5&0&0\\0&5&0\\0&0&5\end{bmatrix}

A(adj. A) = \begin{bmatrix}1&2&2\\2&1&2\\2&2&1\end{bmatrix}\begin{bmatrix}-3&2&2\\2&-3&2\\2&2&-3\end{bmatrix}=\begin{bmatrix}5&0&0\\0&5&0\\0&0&5\end{bmatrix}

Por lo tanto, (adj A)A = |A|I = A(adj A)  

Por lo tanto probado

(ii) 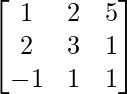\begin{bmatrix}1&2&5\\2&3&1\\-1&1&1\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}1&2&5\\2&3&1\\-1&1&1\end{bmatrix}

Los cofactores de A son

C 11 =  \begin{bmatrix}3&1\\1&1\end{bmatrix}  = 2

C 12 =  \begin{bmatrix}2&1\\-1&1\end{bmatrix}  = -3

C 13 =  \begin{bmatrix}2&3\\-1&1\end{bmatrix}  = 5

C 21 =  \begin{bmatrix}2&5\\1&1\end{bmatrix}  = 3

C 22 =  \begin{bmatrix}1&5\\-1&1\end{bmatrix}  = 6

C 23 =  \begin{bmatrix}1&2\\-1&1\end{bmatrix}  = -3

C 31 =  \begin{bmatrix}2&5\\3&1\end{bmatrix}  = -13

C 32 =  \begin{bmatrix}1&5\\2&1\end{bmatrix}  = 9

C 33 =  \begin{bmatrix}1&2\\2&3\end{bmatrix}  = -1

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}2&-3&5\\3&6&-3\\-13&9&-1\end{bmatrix}^T

=\begin{bmatrix}2&3&-13\\-3&6&9\\5&-3&-1\end{bmatrix}

Para probar, (adj A)A = |A|I = A(adj A)

|A| = 1(3 – 1) – 2(2 + 1) + 5(2 + 3)

= 2 – 6 + 25 = 21

(adj. A)A = \begin{bmatrix}2&3&-13\\-3&6&9\\5&-3&-1\end{bmatrix}\begin{bmatrix}1&2&5\\2&3&1\\-1&1&1\end{bmatrix}=\begin{bmatrix}21&0&0\\0&21&0\\0&0&21\end{bmatrix}

|A|I = (21)\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}=\begin{bmatrix}21&0&0\\0&21&0\\0&0&21\end{bmatrix}

A(adj. A) = \begin{bmatrix}1&2&5\\2&3&1\\-1&1&1\end{bmatrix}\begin{bmatrix}2&3&-13\\-3&6&9\\5&-3&-1\end{bmatrix}=\begin{bmatrix}21&0&0\\0&21&0\\0&0&21\end{bmatrix}

Por lo tanto, (adj A)A = |A|I = A(adj A)  

Por lo tanto probado

(iii) 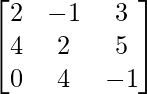\begin{bmatrix}2&-1&3\\4&2&5\\0&4&-1\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}2&-1&3\\4&2&5\\0&4&-1\end{bmatrix}

Los cofactores de A son

C 11 =  \begin{bmatrix}2&5\\4&-1\end{bmatrix}  = -22

C12 = –  = 4\begin{bmatrix}4&5\\0&-1\end{bmatrix}

C 13 =  \begin{bmatrix}4&2\\0&4\end{bmatrix}  = 16

C 21 = – \begin{bmatrix}-1&3\\4&-1\end{bmatrix}  = 11

C 22 =  \begin{bmatrix}2&3\\0&-1\end{bmatrix}  = -2

C 23 = – \begin{bmatrix}2&-1\\0&4\end{bmatrix}  = -8

C 31 =  \begin{bmatrix}-1&3\\2&5\end{bmatrix}  = -11

C 32 = – \begin{bmatrix}2&3\\4&5\end{bmatrix}  = 2

C 33 =  \begin{bmatrix}2&-1\\4&2\end{bmatrix}  = 8

adj A = \begin{bmatrix}-22&4&16\\11&-2&-8\\-11&2&8\end{bmatrix}^T

= \begin{bmatrix}-22&11&-11\\4&-2&2\\16&-8&8\end{bmatrix}

Para probar, (adj A)A = |A|I = A(adj A)

|A| = 2(-2 – 20) + 1(-4 – 0) + 3(16 – 0)

= -44 – 4 + 48 = 0

(adj. A)A = \begin{bmatrix}-22&11&-11\\4&-2&2\\16&-8&8\end{bmatrix}\begin{bmatrix}2&-1&3\\4&2&5\\0&4&-1\end{bmatrix}=\begin{bmatrix}0&0&0\\0&0&0\\0&0&0\end{bmatrix}

|A|I = (0)\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}=\begin{bmatrix}0&0&0\\0&0&0\\0&0&0\end{bmatrix}

A(adj. A) = \begin{bmatrix}2&-1&3\\4&2&5\\0&4&-1\end{bmatrix}\begin{bmatrix}-22&11&-11\\4&-2&2\\16&-8&8\end{bmatrix}=\begin{bmatrix}0&0&0\\0&0&0\\0&0&0\end{bmatrix}

Por lo tanto, (adj A)A = |A|I = A(adj A)  

Por lo tanto probado

(iv) \begin{bmatrix}2&0&-1\\5&1&0\\1&1&3\end{bmatrix}

Solución:

Aquí, A =  \begin{bmatrix}2&0&-1\\5&1&0\\1&1&3\end{bmatrix}

Los cofactores de A son

C 11 =  \begin{bmatrix}1&0\\1&3\end{bmatrix}  = 3

C12 = –  = -15\begin{bmatrix}5&0\\1&3\end{bmatrix}

C 13 =  \begin{bmatrix}5&1\\1&1\end{bmatrix}  = 4

C 21 =  \begin{bmatrix}0&-1\\1&3\end{bmatrix}  = -1

C 22 =  \begin{bmatrix}2&-1\\1&3\end{bmatrix}  = 7

C 23 =  \begin{bmatrix}2&0\\1&1\end{bmatrix}  = -2

C 31 =  \begin{bmatrix}0&-1\\1&0\end{bmatrix}  = 1

C 32 =  \begin{bmatrix}2&-1\\5&0\end{bmatrix}  = -5

C 33 = \begin{bmatrix}2&0\\5&1\end{bmatrix}  = 2

adj A = \begin{bmatrix}3&-15&4\\-1&7&-2\\1&-5&2\end{bmatrix}^T

=\begin{bmatrix}3&-1&1\\-15&7&-5\\4&-2&2\end{bmatrix}

Para probar, (adj A)A = |A|I = A(adj A)

|A| = 2(3 – 0) – 0(15 – 0) – 1(5 – 1)

= 6 – 4 = 2

(adj. A)A = \begin{bmatrix}3&-1&1\\-15&7&-5\\4&-2&2\end{bmatrix}\begin{bmatrix}2&0&-1\\5&1&0\\1&1&3\end{bmatrix}=\begin{bmatrix}2&0&0\\0&2&0\\0&0&2\end{bmatrix}

|A|I = (2)\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}

A (adj. A) = \begin{bmatrix}2&0&-1\\5&1&0\\1&1&3\end{bmatrix}\begin{bmatrix}3&-1&1\\-15&7&-5\\4&-2&2\end{bmatrix}=\begin{bmatrix}2&0&0\\0&2&0\\0&0&2\end{bmatrix}

Por lo tanto, (adj A)A = |A|I = A(adj A)  

Por lo tanto probado

Pregunta 3. Para la array A = 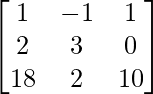\begin{bmatrix}1&-1&1\\2&3&0\\18&2&10\end{bmatrix} , demuestre que A(adj A) = O.

 Solución:

Cofactor de A son, 

C 11 = 30 C 12 = -20 C 13 = -50

C 21 = 12 C 22 = -8 C 23 = -20

C 31 = -3 C 32 = 2 C 33 = 5  

adj A =  \begin{bmatrix}30&-20&-50\\12&-8&-20\\-3&2&5\end{bmatrix}^T

= \begin{bmatrix}30&12&-3\\-20&-8&2\\-50&-20&5\end{bmatrix}

A(adj. A) =  \begin{bmatrix}1&-1&1\\2&3&0\\18&2&10\end{bmatrix} \begin{bmatrix}30&12&-3\\-20&-8&2\\-50&-20&5\end{bmatrix}

= \begin{bmatrix}1&-1&1\\2&3&0\\18&2&10\end{bmatrix}(0)

= 0

Por lo tanto probado

Pregunta 4. Si A = 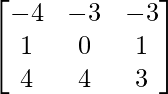\begin{bmatrix}-4&-3&-3\\1&0&1\\4&4&3\end{bmatrix} , demuestre que adj A = A. 

Solución:

Aquí, A = \begin{bmatrix}-4&-3&-3\\1&0&1\\4&4&3\end{bmatrix}

Cofactor de A son,

C 11 = -4 C 12 = 1 C 13 = 4

C 21 = -3 C 22 = 0 C 23 = 4

C 31 = 4 C 32 = 4 C 33 = 3  

adj A = \begin{bmatrix}-4&1&4\\-3&0&4\\-3&1&3\end{bmatrix}^T

= \begin{bmatrix}-4&-3&-3\\1&0&1\\4&4&3\end{bmatrix}

Por lo tanto, adj A = A

Pregunta 5. Si A = 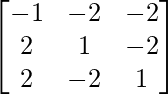 \begin{bmatrix}-1&-2&-2\\2&1&-2\\2&-2&1\end{bmatrix} , demuestre que adj A = 3A T .

Solución:

Aquí, A = \begin{bmatrix}-1&-2&-2\\2&1&-2\\2&-2&1\end{bmatrix}

Cofactor de A son,

C 11 = -3 C 12 = -6 C 13 = -6

C 21 = 6 C 22 = 3 C 23 = -6

C 31 = 6 C 32 = -6 C 33 = 3  

adj A = \begin{bmatrix}-3&-6&-6\\6&3&-6\\6&-6&3\end{bmatrix}^T

= \begin{bmatrix}-3&6&6\\-6&3&-6\\-6&-6&3\end{bmatrix}

UN T = \begin{bmatrix}-1&2&2\\-2&1&-2\\-2&-2&1\end{bmatrix}

Ahora, 3A T = 3 \begin{bmatrix}-1&2&2\\-2&1&-2\\-2&-2&1\end{bmatrix}  = \begin{bmatrix}-3&6&6\\-6&3&-6\\-6&-6&3\end{bmatrix}

adj A = 3.A T 

Por lo tanto probado

Pregunta 6. Encuentra A(adj A) para la array A = 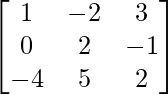\begin{bmatrix}1&-2&3\\0&2&-1\\-4&5&2\end{bmatrix} .

Solución:

Aquí, A = \begin{bmatrix}1&-2&3\\0&2&-1\\-4&5&2\end{bmatrix}

Cofactor de A son,

C 11 = 9 C 12 = 4 C 13 = 8

C 21 = 19 C 22 = 14 C 23 = 3

C 31 = -4 C 32 = 1 C 33 = 2

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}9&4&8\\19&14&3\\-4&1&2\end{bmatrix}^T

= \begin{bmatrix}9&19&-4\\4&14&1\\8&3&2\end{bmatrix}

A(adj. A) = \begin{bmatrix}1&-2&3\\0&2&-1\\-4&5&2\end{bmatrix} \begin{bmatrix}9&19&-4\\4&14&1\\8&3&2\end{bmatrix}

= \begin{bmatrix}25&0&0\\0&25&0\\0&0&25\end{bmatrix}

= 25\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}

= 25I 3

Pregunta 7. Encuentra la inversa de cada una de las siguientes arrays:

(i) 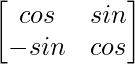\begin{bmatrix}cos θ&sinθ\\-sin θ&cos θ\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}cos θ&sinθ\\-sin θ&cos θ\end{bmatrix}

|A| = cos 2 θ + sen 2 θ = 1

Por lo tanto, el inverso de A existe 

Los cofactores de A son,

Cofactor de A son,

C 11 = cos θ C 12 = sen θ

C 21 = -sen θ C 22 = cos θ

adj A = \begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}^T

= \begin{bmatrix}cos θ&sinθ\\-sin θ&cos θ\end{bmatrix}^T

= \begin{bmatrix}cos θ&-sinθ\\sin θ&cos θ\end{bmatrix}

A – 1 = 1/|A|. adj.

=1/1. \begin{bmatrix}cos θ&-sinθ\\sin θ&cos θ\end{bmatrix}   

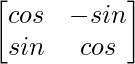
(ii) \begin{bmatrix}0&1\\1&0\end{bmatrix}     

Solución:

Aquí, A = \begin{bmatrix}0&1\\1&0\end{bmatrix}   

|A| = -1

Por lo tanto, el inverso de A existe  

Cofactor de A son,

C11 = 0 C12 = -1

C21 = -1 C22 = 0

adj A = \begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}^T

= \begin{bmatrix}0&-1\\-1&0\end{bmatrix}^T

= \begin{bmatrix}0&-1\\-1&0\end{bmatrix}

A – 1 = 1/|A|. adj.

= \frac{1}{-1}\begin{bmatrix}0&-1\\-1&0\end{bmatrix}

= \begin{bmatrix}0&1\\1&0\end{bmatrix}

(iii) \begin{bmatrix}a&b\\c&\frac{(a+bc)}{a}\end{bmatrix}

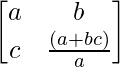
Solución:

Aquí, A = \begin{bmatrix}a&b\\c&\frac{(a+bc)}{a}\end{bmatrix}       

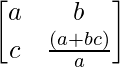
|A| = a(1 + bc)/a – bc = 1 + bc – bc = 1

Por lo tanto, existe el inverso de A.  

Cofactor de A son,

C 11 = (1 + bc)/a C 12 = -c

C 21 = -b C 22 = un

adj A =\begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}^T

= \begin{bmatrix}\frac{(a+bc)}{a} &-c\\-b&a\end{bmatrix}^T

= \begin{bmatrix}\frac{(a+bc)}{a}&-b\\-c&a\end{bmatrix}

A – 1 = 1/|A|. adj.

= 1/1 \begin{bmatrix}\frac{(a+bc)}{a}&-b\\-c&a\end{bmatrix}

= \begin{bmatrix}\frac{(a+bc)}{a}&-b\\-c&a\end{bmatrix}

(iv) \begin{bmatrix}2&5\\-3&1\end{bmatrix}

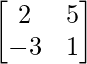
Solución:

Aquí, A = \begin{bmatrix}2&5\\-3&1\end{bmatrix}

|A| = 2 + 15 = 17

Por lo tanto, existe el inverso de A.  

Cofactor de A son,

C 11 = 1 C 12 = 3

C 21 = -5 C 22 = 2

adj A = \begin{bmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{bmatrix}^T

= \begin{bmatrix}1&3\\-5&2\end{bmatrix}^T       

= \begin{bmatrix}1&-5\\3&2\end{bmatrix}

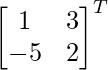
A – 1 = 1/|A|. adj.

= \frac{1}{17}\begin{bmatrix}1&-5\\3&2\end{bmatrix}

= \begin{bmatrix}\frac{1}{17}&\frac{-5}{17}\\\frac{3}{17}&\frac{2}{17}\end{bmatrix}

Pregunta 8. Encuentra la inversa de cada una de las siguientes arrays.

(i) \begin{bmatrix}1&2&3\\2&3&1\\3&1&2\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}1&2&3\\2&3&1\\3&1&2\end{bmatrix}

|A| = 1(6 – 1) – 2(4 – 3) + 3(2 – 9)

= 5 – 2 – 21 = -18

Por lo tanto, existe el inverso de A

Los cofactores de A son:

C 11 = 5 C 12 = -1 C 13 = -7

C 21 = -1 C 22 = -7 C 23 = 5

C 31 = -7 C 32 = 5 C 33 = -1  

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}5&-1&-7\\-1&-7&5\\-7&5&-1\end{bmatrix}^T

= \begin{bmatrix}5&-1&-7\\-1&-7&5\\-7&5&-1\end{bmatrix}

A – 1 = 1/|A|. adj.

Por lo tanto, A – 1 = \frac{1}{-18}\begin{bmatrix}5&-1&-7\\-1&-7&5\\-7&5&-1\end{bmatrix}

=\begin{bmatrix}-5/18&1/18&7/18\\1/18&7/18&-5/18\\7/18&-5/18&1/18\end{bmatrix}   

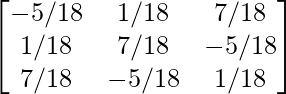
(ii) 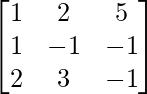 \begin{bmatrix}1&2&5\\1&-1&-1\\2&3&-1\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}1&2&5\\1&-1&-1\\2&3&-1\end{bmatrix}

|A| = 1(1 + 3) – 2(-1 + 2) + 5(3 + 2)

= 4 – 2 – 25 = 27

Por lo tanto, existe el inverso de A

Los cofactores de A son:

C 11 = 4 C 12 = -1 C 13 = 5

C 21 = -17 C 22 = -11 C 23 = 1

C 31 = 3 C 32 = 6 C 33 = -3

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}4&-1&5\\17&-11&1\\3&6&-3\end{bmatrix}^T

= \begin{bmatrix}4&17&3\\-1&-11&6\\5&1&-3\end{bmatrix}

A – 1 = 1/|A|. adj.

Por lo tanto, A – 1 = \frac{1}{27}\begin{bmatrix}4&17&3\\-1&-11&6\\5&1&-3\end{bmatrix}

= \begin{bmatrix}4/27&17/27&3/27\\-1/27&-11/27&6/27\\5/27&1/27&-3/27\end{bmatrix}

= \begin{bmatrix}4/27&17/27&1/9\\-1/27&-11/27&2/9\\5/27&1/27&-1/9\end{bmatrix}   

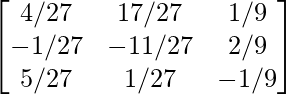
(iii) 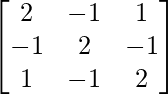\begin{bmatrix}2&-1&1\\-1&2&-1\\1&-1&2\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}2&-1&1\\-1&2&-1\\1&-1&2\end{bmatrix}

|A| = 2(4 – 1) – (-1)(-2 + 1) + 1(1 – 2)

= 6 – 1 – 1 = 4

Por lo tanto, existe el inverso de A

Los cofactores de A son:

C 11 = 3 C 12 = 1 C 13 = -1

C 21 = 1 C 22 = 3 C 23 = 1

C 31 = -1 C 32 = 1 C 33 = 3

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}3&1&-1\\1&3&1\\-1&1&3\end{bmatrix}^T

= \begin{bmatrix}3&1&-1\\1&3&1\\-1&1&3\end{bmatrix}

A – 1 = 1/|A|. adj.

Por lo tanto, A – 1 = \frac{1}{4}\begin{bmatrix}3&1&-1\\1&3&1\\-1&1&3\end{bmatrix}

= \begin{bmatrix}3/4&1/4&-1/4\\1/4&3/4&1/4\\-1/4&1/4&3/4\end{bmatrix}    

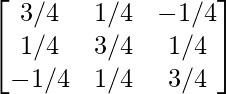
(iv) 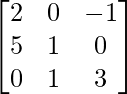\begin{bmatrix}2&0&-1\\5&1&0\\0&1&3\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}2&-1&1\\-1&2&-1\\1&-1&2\end{bmatrix}

|A| = 2(3 – 0) – 0 + 1(5)

= 6 – 5 = 1

Por lo tanto, existe el inverso de A

Los cofactores de A son:

C 11 = 3 C 12 = -15 C 13 = 5

C 21 = -1 C 22 = 6 C 23 = -2

C 31 = 1 C 32 = -5 C 33 = 2

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}3&-15&5\\-1&6&-2\\1&-5&2\end{bmatrix}^T

= \begin{bmatrix}3&-1&1\\-15&6&-5\\5&-2&2\end{bmatrix}

A – 1 = 1/|A|. adj.

Por lo tanto, A – 1 = \frac{1}{1}\begin{bmatrix}3&-1&1\\-15&6&-5\\5&-2&2\end{bmatrix}

= \begin{bmatrix}3&-1&1\\-15&6&-5\\5&-2&2\end{bmatrix}   

(v) \begin{bmatrix}0&1&-1\\4&-3&4\\3&-3&4\end{bmatrix}

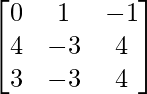
Solución:

Aquí, A = \begin{bmatrix}0&1&-1\\4&-3&4\\3&-3&4\end{bmatrix}

|A| = 0 – 1(16 – 12) – 1(-12 + 9)

= -4 + 3 = -1

Por lo tanto, existe el inverso de A

Los cofactores de A son:

C 11 = 0 C 12 = -4 C 13 = -3

C 21 = -1 C 22 = 3 C 23 = 3

C 31 = 1 C 32 = -4 C 33 = -4

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}0&-4&-3\\-1&3&3\\1&-4&-4\end{bmatrix}^T

= \begin{bmatrix}0&-1&1\\-4&3&-4\\-3&3&-4\end{bmatrix}

A – 1 = 1/|A|. adj.

Por lo tanto, A – 1 = \frac{1}{-1}\begin{bmatrix}0&-1&1\\-4&3&-4\\-3&3&-4\end{bmatrix}

= \begin{bmatrix}0&-1&1\\-4&3&-4\\-3&3&-4\end{bmatrix}          

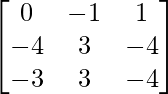
(vi) 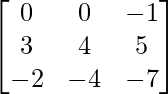\begin{bmatrix}0&0&-1\\3&4&5\\-2&-4&-7\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}0&0&-1\\3&4&5\\-2&-4&-7\end{bmatrix}

|A| = 0 – 0 – 1(-12 + 8)

= -1(-4) = 4

Por lo tanto, existe el inverso de A

Los cofactores de A son:

C 11 = -8 C 12 = 11 C 13 = -4

C 21 = 4 C 22 = -2 C 23 = 0

C 31 = 4 C 32 = -3 C 33 = 0

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}-8&11&-4\\4&-2&0\\4&-3&0\end{bmatrix}^T

= \begin{bmatrix}-8&4&4\\11&-2&-3\\-4&0&-0\end{bmatrix}

A – 1 = 1/|A|. adj.

Por lo tanto, A – 1 = \frac{1}{4}\begin{bmatrix}-8&4&4\\11&-2&-3\\-4&0&-0\end{bmatrix}

= \begin{bmatrix}-2&1&1\\11/4&-1/2&-3/4\\-1&0&-0\end{bmatrix}   

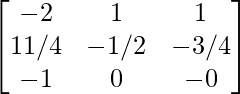
(vii) 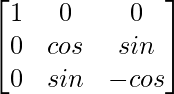 \begin{bmatrix}1&0&0\\0&cosα &sinα\\0&sinα&-cosα \end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}1&0&0\\0&cosα &sinα\\0&sinα&-cosα \end{bmatrix}

|A| = -cos 2 α – sen 2 α

= -(cos 2 α + sen 2 α) = -1

Por lo tanto, existe el inverso de A

Los cofactores de A son:  

C 11 = -1 C 12 = 0 C 13 = -0

C 21 = 0 C 22 = -cosα C 23 = -sinα

C 31 = 0 C 32 = -sinα C 33 = cosα

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}-1&0&0\\0&- cosα &- sinα \\0&-sinα & cosα \end{bmatrix}^T

= \begin{bmatrix}-1&0&0\\0&- cosα &- sinα \\0&-sinα & cosα \end{bmatrix}

A – 1 = 1/|A|. adj.

Por lo tanto, A – 1 = \frac{1}{-1}\begin{bmatrix}-1&0&0\\0&- cosα &- sinα \\0&-sinα & cosα \end{bmatrix}

= \begin{bmatrix}1&0&0\\0&cosα &sinα \\0&sinα &-cosα \end{bmatrix}       

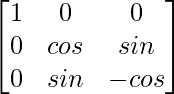
Pregunta 9. (i) 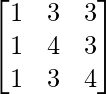\begin{bmatrix}1&3&3\\1&4&3\\1&3&4\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}1&3&3\\1&4&3\\1&3&4\end{bmatrix}

|A| = 1(16 – 9) – 3(4 – 3) + 3(3 – 4)

= 7 – 3 – 3 = 1

Por lo tanto, existe el inverso de A

Los cofactores de A son:

C 11 = 7 C 12 = -1 C 13 = -1

C 21 = -3 C 22 = 1 C 23 = 0

C 31 = -3 C 32 = 0 C 33 = 1

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}7&-1&-1\\-3&1&0\\-3&0&1\end{bmatrix}^T

= \begin{bmatrix}7&-3&-3\\-1&1&0\\-1&0&1\end{bmatrix}

A – 1 = 1/|A|. adj.

Por lo tanto, A -1 = 1/1\begin{bmatrix}7&-3&-3\\-1&1&0\\-1&0&1\end{bmatrix}

=\begin{bmatrix}7&-3&-3\\-1&1&0\\-1&0&1\end{bmatrix}

Para verificar A -1 A = \begin{bmatrix}7&-3&-3\\-1&1&0\\-1&0&1\end{bmatrix} \begin{bmatrix}1&3&3\\1&4&3\\1&3&4\end{bmatrix}

= \begin{bmatrix}7-3-3&21-12-9&21-9-12\\-1+1&-3+4&-3+3\\-1+1&-3+3&-3+4\end{bmatrix}

= \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}         

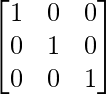
(ii) \begin{bmatrix}2&3&1\\3&4&1\\3&7&2\end{bmatrix}

Solución:

Aquí, A = \begin{bmatrix}2&3&1\\3&4&1\\3&7&2\end{bmatrix}

|A| = 2(8 – 7) – 3(6 – 3) + 1(21 – 12)

= 2 – 3(3) + 1(9) = 2

Por lo tanto, existe el inverso de A

Los cofactores de A son:

C 11 = 1 C 12 = -3 C 13 = 9

C 21 = 1 C 22 = 1 C 23 = -5

C 31 = -1 C 32 = 1 C 33 = -1

adj A = \begin{bmatrix}C_{11}&C_{12}&C_{13}\\C_{21}&C_{22}&C_{23}\\C_{31}&C_{32}&C_{34}\end{bmatrix}^T

= \begin{bmatrix}1&-3&9\\1&1&-5\\-1&1&-1\end{bmatrix}^T

= \begin{bmatrix}1&1&-1\\-3&1&1\\9&-5&-1\end{bmatrix}

A – 1 = 1/|A|. adj.

Por lo tanto, A – 1 = \frac{1}{2}\begin{bmatrix}1&1&-1\\-3&1&1\\9&-5&-1\end{bmatrix}

Para verificar A -1 A = \frac{1}{2}\begin{bmatrix}1&1&-1\\-3&1&1\\9&-5&-1\end{bmatrix} \begin{bmatrix}2&3&1\\3&4&1\\3&7&2\end{bmatrix}

= \frac{1}{2}\begin{bmatrix}2+3-3&3+4-7&1+1-2\\-6+3+3&-9+4+7&-3+1+2\\18-15-3&27-20-7&9-5-2\end{bmatrix}

= \begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}     

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *