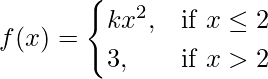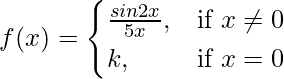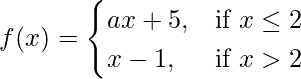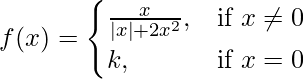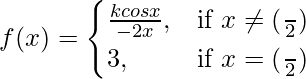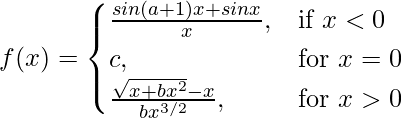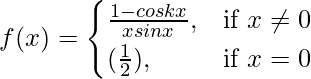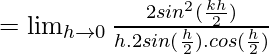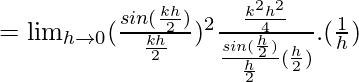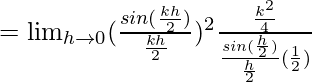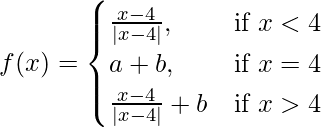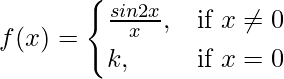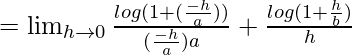Clase 12 Soluciones RD Sharma – Capítulo 9 Continuidad – Ejercicio 9.1

Pregunta 16. Discutir la continuidad de la función.

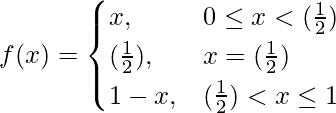$f(x)=\begin{cases}x,&0\leq x<(\frac{1}{2}) \\(\frac{1}{2}),&x=(\frac{1}{2}) \\1-x,&(\frac{1}{2})<x\leq1\end{cases}$ en el punto x = 1/2.

Solución:

Dado que,

$f(x)=\begin{cases}x,&0\leq x<(\frac{1}{2}) \\(\frac{1}{2}),&x=(\frac{1}{2}) \\1-x,&(\frac{1}{2})<x\leq1\end{cases}$

Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 1/2,

Consideremos LHL,

$\lim_{x\to{\frac{1}{2}}^-}f(x) =\lim_{h\to0}f(\frac{1}{2}-h)$

$=\lim_{h\to0}\frac{1}{2}-h=\frac{1}{2}$

Ahora, consideremos la BSR,

$\lim_{x\to{\frac{1}{2}}^+}f(x) =\lim_{h\to0}f(\frac{1}{2}+h)$

$=\lim_{h\to0}1-(\frac{1}{2}+h)=\frac{1}{2}$

f(1/2) = 1/2

Así, LHL= RHL = f(1/2) = 1/2

Por lo tanto, la f(x) es continua en x = 1/2.

Pregunta 17. Discuta la continuidad de $f(x)=\begin{cases}2x-1,& \text{if }x<0 \\2x+1,& \text{if }x\geq0\end{cases}$ en el punto x = 0.

Solución:

Dado que,

$f(x)=\begin{cases}2x-1,& \text{if }x<0 \\2x+1,& \text{if }x\geq0\end{cases}$

Entonces, aquí comprobamos la continuidad de la f(x) dada en x = 10,

Consideremos LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}2(-h)-1=-1$

Ahora, consideremos la BSR,

$\lim_{x\to0^+}f(x) =\lim_{h\to0}f(0+h)$

$=\lim_{h\to0}2h+1=1$

Por lo tanto, LHL ≠ RHL

Por lo tanto, f(x) es discontinua en x = 0.

Pregunta 18. ¿Para qué valor de k la función es $f(x)=\begin{cases}\frac{x^2-1}{x-1},& x\neq1 \\k,& x=1\end{cases}$ continua en x = 1?

Solución:

Dado que,

$f(x)=\begin{cases}\frac{x^2-1}{x-1},& x\neq1 \\k,& x=1\end{cases}$

Además, f(x) es continua en x = 1

Asi que,

LHL = RHL = f(1) ……(i)

Consideremos LHL,

$\lim_{x\to1^-}f(x) =\lim_{h\to0}f(1-h)$

$=\lim_{h\to0}\frac{(1-h)^2-1}{(1-h)-1}$

$=\lim_{h\to0}\frac{h^2-2h}{-h}=2$

f(1) = k

De la ecuación (i), obtenemos

HL = F(1)

Por lo tanto, k = 2

Pregunta 19. Determinar el valor de la constante k para que la función

$f(x)=\begin{cases}\frac{x^2-3x+2}{x-1},& \text{if }x\neq1 \\k,& \text{if }x=1\end{cases}$ continua en x = 1.

Solución:

Dado que,

$f(x)=\begin{cases}\frac{x^2-3x+2}{x-1},& \text{if }x\neq1 \\k,& \text{if }x=1\end{cases}$

Además, f(x) es continua en x = 1

Entonces, LHL = RHL = f(1) …..(i)

Consideremos LHL,

$\lim_{x\to1^-}f(x) =\lim_{h\to0}f(1-h)$

$=\lim_{h\to0}\frac{(1-h)^2-3(1-h)+2}{(1-h)-1}$

$=\lim_{h\to0}\frac{h^2+h}{-h}$

$=\lim_{h\to0}-h-1=-1$

f(1) = k

De la ecuación (i), obtenemos

HL = F(1)

Por lo tanto, k = -1

Pregunta 20. ¿Para qué valor de k la función es 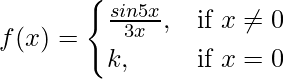$f(x)=\begin{cases}\frac{sin5x}{3x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ continua en x = 0?

Solución:

Dado que,

$f(x)=\begin{cases}\frac{sin5x}{3x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$

Además, f(x) es continua en x = 0

Entonces, LHL = RHL = f(0) …..(i)

Consideremos LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}\frac{sin5(-h)}{3(-h)}$

$=\lim_{h\to0}\frac{-sin5h}{-3h}$

$=\lim_{h\to0}\frac{sin5h}{3h}\frac{5h}{3h}=\frac{5}{3}$

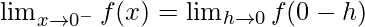
f(0) = k

Por lo tanto, de la ecuación (i), obtenemos

k = 5/3

Por lo tanto, k = 5/3

Pregunta 21. Determinar el valor de la constante k para que la función

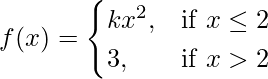$f(x)=\begin{cases}kx^2,& \text{if }x\leq2 \\3,& \text{if }x>2\end{cases}$ continua en x = 2.

Solución:

Dado que,

$f(x)=\begin{cases}kx^2,& \text{if }x\leq2 \\3,& \text{if }x>2\end{cases}$

Además, f(x) es continua en x = 2

Entonces, f(2) = k(2) ² = 4k

$\lim_{x\to2^-}f(x)=\lim_{x\to2^+}f(x)=f(2)$

⇒ $\lim_{x\to2^-}(kx^2)=\lim_{x\to2^+}(3)=4k$

⇒ k × 2 ² = 3 = 4k

⇒ 4k = 3 = 4k

⇒ 4k = 3

⇒ k = 3/4

Por lo tanto, el valor de k es 3/4

Pregunta 22. Determinar el valor de la constante k para que la función

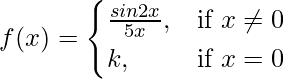$f(x)=\begin{cases}\frac{sin2x}{5x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ es continua en x = 0.

Solución:

Dado que,

$f(x)=\begin{cases}\frac{sin2x}{5x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$

Además, f(x) es continua en x = 0

Entonces, LHL = RHL = f(0) ….(i)

Consideremos LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}\frac{sin2(-h)}{5(-h)}$

$=\lim_{h\to0}\frac{-sin2h}{-5h}$

$=\lim_{h\to0}\frac{sin2h}{5h}×\frac{2h}{5h}=2/5$

f(0) = k

De la ecuación (i), obtenemos

k = 2/5

Pregunta 23. Encuentra los valores de a para que la función 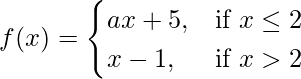$f(x)=\begin{cases}ax+5,& \text{if }x\leq2 \\x-1,& \text{if }x>2\end{cases}$ sea continua en x = 2.

Solución:

Dado que,

$f(x)=\begin{cases}ax+5,& \text{if }x\leq2 \\x-1,& \text{if }x>2\end{cases}$

Además, f(x) es continua en x = 2

Entonces, LHL = RHL = f(2) …….(i)

Consideremos LHL,

$\lim_{x\to2^-}f(x) =\lim_{h\to0}f(2-h)$

$=\lim_{h\to0}a(2-h)+5$

= 2a + 5

Ahora, consideremos la BSR,

$\lim_{x\to2^+}f(x) =\lim_{h\to0}f(2+h)$

$=\lim_{h\to0}2+h-1=1$

De la ecuación (i), obtenemos

2a + 5 = 1

⇒ a = -2

Pregunta 24. Demuestra que la función

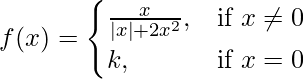$f(x)=\begin{cases}\frac{x}{|x|+2x^2},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ permanece discontinua en x = 0, independientemente de la elección de k.

Solución:

Dado que,

$f(x)=\begin{cases}\frac{x}{|x|+2x^2},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$

Tenemos, en x = 0

Consideremos LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}\frac{-h}{|-h|+2(-h)^2}$

$=\lim_{h\to0}\frac{-h}{h+2h^2}$

$=\lim_{h\to0}\frac{-1}{1+2h}=-1$

f(0) = k

Ahora, consideremos la BSR,

$\lim_{x\to0^+}f(x) =\lim_{h\to0}f(0+h)$

$=\lim_{h\to0}\frac{h}{|h|+2h^2}$

$=\lim_{h\to0}\frac{1}{1+2h}=1$

Dado que, LHL ≠ RHL,

Por lo tanto, f(x) seguirá siendo discontinua en x = 0, independientemente del valor de k.

Pregunta 25. Encuentra el valor de k si f(x) es continua en x = π/2, donde

$f(x)=\begin{cases}\frac{kcosx}{π-2x},& \text{if }x\neq(\frac{π}{2}) \\3,& \text{if }x=(\frac{π}{2})\end{cases}$

Solución:

Dado que,

$f(x)=\begin{cases}\frac{kcosx}{π-2x},& \text{if }x\neq(\frac{π}{2}) \\3,& \text{if }x=(\frac{π}{2})\end{cases}$

Además, f(x) es continua en x = π/2

LHL = RHL

⇒ $\lim_{x\to{\frac{π}{2}}^-}f(x)=\lim_{x\to{\frac{π}{2}}^+}f(x)=\lim_{h\to{\frac{π}{2}}}f(x)=f(\frac{π}{2})$

⇒ $\lim_{x\to{\frac{π}{2}}^-}\frac{kcosx}{π-2x}=3$

⇒ $k\lim_{x\to\frac{π}{2}}\frac{sin(\frac{π}{2}-x)}{2(\frac{π}{2}-x)}=3$

⇒ $\frac{k}{2}\lim_{x\to\frac{π}{2}}\frac{sin(\frac{π}{2}-x)}{(\frac{π}{2}-x)}=3$

⇒ k/2 = 3

⇒ k = 6

Pregunta 26. Determine los valores de a, b, c para los cuales la función

$f(x)=\begin{cases}\frac{sin(a+1)x+sinx}{x},& \text{if }x<0 \\c,& \text{for }x=0\\\frac{\sqrt{x+bx^2}-√x}{bx^{3/2}},&\text{for }x>0\end{cases}$

es continua en x = 0.

Solución:

Dado que,

$f(x)=\begin{cases}\frac{sin(a+1)x+sinx}{x},& \text{if }x<0 \\c,& \text{for }x=0\\\frac{\sqrt{x+bx^2}-√x}{bx^{3/2}},&\text{for }x>0\end{cases}$

Además, f(x) es continua en x = 0

Entonces, LHL = RHL = f(0) …..(i)

f(0) = 0

Consideremos LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

= $\lim_{h\to0}\frac{sin(a+1)(-h)+sin(-h)}{-h}$

= $\lim_{h\to0}\frac{-sin(ah+h)-sinh}{-h}$

= $\lim_{h\to0}\frac{sin(a+1)h}{h}+\lim_{h\to0}\frac{sinh}{h}$

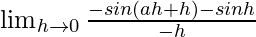
= un + 1 + 1 = un + 2

Ahora, consideremos la BSR,

$\lim_{x\to0^+}f(x) =\lim_{h\to0}f(0+h)$

= $\lim_{h\to0}\frac{\sqrt{h+bh^2}-√h}{bh^{3/2}}$

= $\lim_{h\to0}\frac{\sqrt{h+bh^2}-√h}{bh^{3/2}}\frac{\sqrt{h+bh^2}+√h}{\sqrt{h+bh^2}+√h}$

= $\lim_{h\to0}\frac{h+bh^2-h}{bh^{3/2}(\sqrt{h+bh^2}+√h)}$

= $\lim_{h\to0}\frac{bh^2}{bh^2(\sqrt{1+bh}+1)}=1/2$

De la ecuación (i), obtenemos

a + 2 = 1/2 ⇒ a = -3/2

c = 1/2 y b ∈ R -{0}

Por tanto, a = -3/2, b ∈ R -{0}, c =1/2

Pregunta 27. Si 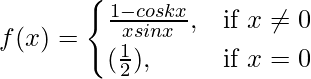$f(x)=\begin{cases}\frac{1-coskx}{xsinx},& \text{if }x\neq0 \\(\frac{1}{2}),& \text{if }x=0\end{cases}$ es continua en x = 0, encuentra k.

Solución:

Dado que,

$f(x)=\begin{cases}\frac{1-coskx}{xsinx},& \text{if }x\neq0 \\(\frac{1}{2}),& \text{if }x=0\end{cases}$

Además, f(x) es continua en x = 0

Entonces, LHL = RHL = f(0) …….(i)

f(0) = 1/2

Consideremos LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}\frac{1-cosk(-h)}{-hsin(-h)}$

$=\lim_{h\to0}\frac{1-coskh}{hsinh}$

$=\lim_{h\to0}\frac{2sin^2(\frac{kh}{2})}{h.2sin(\frac{h}{2}).cos(\frac{h}{2})}$

$=\lim_{h\to0}(\frac{sin(\frac{kh}{2})}{\frac{kh}{2}})^2\frac{\frac{k^2h^2}{4}}{\frac{sin(\frac{h}{2})}{\frac{h}{2}}(\frac{h}{2})}.(\frac{1}{h})$

$=\lim_{h\to0}(\frac{sin(\frac{kh}{2})}{\frac{kh}{2}})^2\frac{\frac{k^2}{4}}{\frac{sin(\frac{h}{2})}{\frac{h}{2}}(\frac{1}{2})}$

= k ² /2

Usando la ecuación (i) obtenemos,

^{k2/ 2} = 1/2 ⇒ k = ± 1

Pregunta 28. Si es 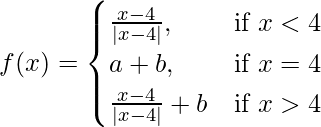$f(x)=\begin{cases}\frac{x-4}{|x-4|},& \text{if }x<4 \\a+b,& \text{if }x=4\\\frac{x-4}{|x-4|}+b& \text{if }x>4\end{cases}$ continua en x = 4, encuentra a, b.

Solución:

Dado que,

$f(x)=\begin{cases}\frac{x-4}{|x-4|},& \text{if }x<4 \\a+b,& \text{if }x=4\\\frac{x-4}{|x-4|}+b& \text{if }x>4\end{cases}$

Además, f(x) es continua en x = 4

Entonces, LHL = RHL = f(4) ……(i)

f(4) = a + b …..(ii)

Consideremos LHL,

$\lim_{x\to4^-}f(x) =\lim_{h\to0}f(4-h)$

$=\lim_{h\to0}\frac{(4-h)-4}{|(4-h)-4|}+a$

$=\lim_{h\to0}\frac{-h}{h}+a$

= a – 1 ……(iii)

Ahora, consideremos la BSR,

$\lim_{x\to4^+}f(x) =\lim_{h\to0}f(4+h)$

$=\lim_{h\to0}\frac{(4+h)-4}{|(4+h)-4|}+b$

$=\lim_{h\to0}\frac{h}{h}+b$

= b + 1 ……(iv)

De la ecuación (i), obtenemos

a – 1 = b + 1 ⇒ a – b = 2 …..(v)

De la ecuación (ii) y la ecuación (iii), obtenemos

a + b = a – 1 ⇒ a – b = -1

De la ecuación (ii) y (iv), obtenemos

un + segundo = segundo + 1 ⇒ un = 1

Así, a = 1 y b = -1

Pregunta 29. ¿Para qué valor de k es la función

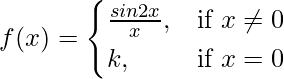$f(x)=\begin{cases}\frac{sin2x}{x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ continua en x = 0 ?

Solución:

Dado que,

$f(x)=\begin{cases}\frac{sin2x}{x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$

Además, f(x) es continua en x = 0

Entonces, LHL = RHL = f(0) …..(i)

f(0) = k

Consideremos LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}\frac{sin2(0-h)}{-h}$

$=\lim_{h\to0}\frac{-sin2h}{-h}=2$

Usando la ecuación (i), obtenemos

k = 2

Pregunta 30. Sea f(x) = 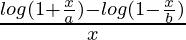$\frac{log(1+\frac{x}{a})-log(1-\frac{x}{b})}{x}$ , x ≠ 0. Encuentra el valor de f en x = 0 para que f se vuelva continua en x = 0.

Solución:

Dado que,

f(x) = $\frac{log(1+\frac{x}{a})-log(1-\frac{x}{b})}{x}$

Además, f(x) es continua en x = 0

Entonces, LHL=RHL=f(0) ….(i)

Consideremos LHL,

$\lim_{x\to0^-}f(x) =\lim_{h\to0}f(0-h)$

$=\lim_{h\to0}\frac{log(1-\frac{h}{a})-log(1+\frac{h}{b})}{-h}$

$=\lim_{h\to0}\frac{log(1+(\frac{-h}{a}))}{(\frac{-h}{a})a}+\frac{log(1+\frac{h}{b})}{h}$

= 1/a + 1/b = (a + b)/ab

De la ecuación (i), obtenemos

f(0) = (a + b)/ab

Publicación traducida automáticamente

Artículo escrito por rahulsharma1771996 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 9 Continuidad – Ejercicio 9.1 | conjunto 2

Pregunta 16. Discutir la continuidad de la función.

$f(x)=\begin{cases}x,&0\leq x<(\frac{1}{2}) \\(\frac{1}{2}),&x=(\frac{1}{2}) \\1-x,&(\frac{1}{2})<x\leq1\end{cases}$ en el punto x = 1/2.

Pregunta 17. Discuta la continuidad de $f(x)=\begin{cases}2x-1,& \text{if }x<0 \\2x+1,& \text{if }x\geq0\end{cases}$ en el punto x = 0.

Pregunta 18. ¿Para qué valor de k la función es $f(x)=\begin{cases}\frac{x^2-1}{x-1},& x\neq1 \\k,& x=1\end{cases}$ continua en x = 1?

Pregunta 19. Determinar el valor de la constante k para que la función

$f(x)=\begin{cases}\frac{x^2-3x+2}{x-1},& \text{if }x\neq1 \\k,& \text{if }x=1\end{cases}$ continua en x = 1.

Pregunta 20. ¿Para qué valor de k la función es $f(x)=\begin{cases}\frac{sin5x}{3x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ continua en x = 0?

Pregunta 21. Determinar el valor de la constante k para que la función

$f(x)=\begin{cases}kx^2,& \text{if }x\leq2 \\3,& \text{if }x>2\end{cases}$ continua en x = 2.

Pregunta 22. Determinar el valor de la constante k para que la función

$f(x)=\begin{cases}\frac{sin2x}{5x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ es continua en x = 0.

Pregunta 23. Encuentra los valores de a para que la función $f(x)=\begin{cases}ax+5,& \text{if }x\leq2 \\x-1,& \text{if }x>2\end{cases}$ sea continua en x = 2.

Pregunta 24. Demuestra que la función

$f(x)=\begin{cases}\frac{x}{|x|+2x^2},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ permanece discontinua en x = 0, independientemente de la elección de k.

Pregunta 25. Encuentra el valor de k si f(x) es continua en x = π/2, donde

$f(x)=\begin{cases}\frac{kcosx}{π-2x},& \text{if }x\neq(\frac{π}{2}) \\3,& \text{if }x=(\frac{π}{2})\end{cases}$

Pregunta 26. Determine los valores de a, b, c para los cuales la función

$f(x)=\begin{cases}\frac{sin(a+1)x+sinx}{x},& \text{if }x<0 \\c,& \text{for }x=0\\\frac{\sqrt{x+bx^2}-√x}{bx^{3/2}},&\text{for }x>0\end{cases}$

es continua en x = 0.

Pregunta 27. Si $f(x)=\begin{cases}\frac{1-coskx}{xsinx},& \text{if }x\neq0 \\(\frac{1}{2}),& \text{if }x=0\end{cases}$ es continua en x = 0, encuentra k.

Pregunta 28. Si es $f(x)=\begin{cases}\frac{x-4}{|x-4|},& \text{if }x<4 \\a+b,& \text{if }x=4\\\frac{x-4}{|x-4|}+b& \text{if }x>4\end{cases}$ continua en x = 4, encuentra a, b.

Pregunta 29. ¿Para qué valor de k es la función

$f(x)=\begin{cases}\frac{sin2x}{x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ continua en x = 0 ?

Pregunta 30. Sea f(x) = $\frac{log(1+\frac{x}{a})-log(1-\frac{x}{b})}{x}$ , x ≠ 0. Encuentra el valor de f en x = 0 para que f se vuelva continua en x = 0.

Deja una respuesta Cancelar la respuesta

Pregunta 16. Discutir la continuidad de la función.

en el punto x = 1/2.

Pregunta 17. Discuta la continuidad de en el punto x = 0.

Pregunta 18. ¿Para qué valor de k la función es continua en x = 1?

Pregunta 19. Determinar el valor de la constante k para que la función

continua en x = 1.

Pregunta 20. ¿Para qué valor de k la función es continua en x = 0?

Pregunta 21. Determinar el valor de la constante k para que la función

continua en x = 2.

Pregunta 22. Determinar el valor de la constante k para que la función

es continua en x = 0.

Pregunta 23. Encuentra los valores de a para que la función sea continua en x = 2.

Pregunta 24. Demuestra que la función

permanece discontinua en x = 0, independientemente de la elección de k.

Pregunta 25. Encuentra el valor de k si f(x) es continua en x = π/2, donde

Pregunta 26. Determine los valores de a, b, c para los cuales la función

es continua en x = 0.

Pregunta 27. Si es continua en x = 0, encuentra k.

Pregunta 28. Si es continua en x = 4, encuentra a, b.

Pregunta 29. ¿Para qué valor de k es la función

continua en x = 0 ?

Pregunta 30. Sea f(x) = , x ≠ 0. Encuentra el valor de f en x = 0 para que f se vuelva continua en x = 0.

Deja una respuesta Cancelar la respuesta

$f(x)=\begin{cases}x,&0\leq x<(\frac{1}{2}) \\(\frac{1}{2}),&x=(\frac{1}{2}) \\1-x,&(\frac{1}{2})<x\leq1\end{cases}$ en el punto x = 1/2.

Pregunta 17. Discuta la continuidad de $f(x)=\begin{cases}2x-1,& \text{if }x<0 \\2x+1,& \text{if }x\geq0\end{cases}$ en el punto x = 0.

Pregunta 18. ¿Para qué valor de k la función es $f(x)=\begin{cases}\frac{x^2-1}{x-1},& x\neq1 \\k,& x=1\end{cases}$ continua en x = 1?

$f(x)=\begin{cases}\frac{x^2-3x+2}{x-1},& \text{if }x\neq1 \\k,& \text{if }x=1\end{cases}$ continua en x = 1.

Pregunta 20. ¿Para qué valor de k la función es $f(x)=\begin{cases}\frac{sin5x}{3x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ continua en x = 0?

$f(x)=\begin{cases}kx^2,& \text{if }x\leq2 \\3,& \text{if }x>2\end{cases}$ continua en x = 2.

$f(x)=\begin{cases}\frac{sin2x}{5x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ es continua en x = 0.

Pregunta 23. Encuentra los valores de a para que la función $f(x)=\begin{cases}ax+5,& \text{if }x\leq2 \\x-1,& \text{if }x>2\end{cases}$ sea continua en x = 2.

$f(x)=\begin{cases}\frac{x}{|x|+2x^2},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ permanece discontinua en x = 0, independientemente de la elección de k.

Pregunta 27. Si $f(x)=\begin{cases}\frac{1-coskx}{xsinx},& \text{if }x\neq0 \\(\frac{1}{2}),& \text{if }x=0\end{cases}$ es continua en x = 0, encuentra k.

Pregunta 28. Si es $f(x)=\begin{cases}\frac{x-4}{|x-4|},& \text{if }x<4 \\a+b,& \text{if }x=4\\\frac{x-4}{|x-4|}+b& \text{if }x>4\end{cases}$ continua en x = 4, encuentra a, b.

$f(x)=\begin{cases}\frac{sin2x}{x},& \text{if }x\neq0 \\k,& \text{if }x=0\end{cases}$ continua en x = 0 ?

Pregunta 30. Sea f(x) = $\frac{log(1+\frac{x}{a})-log(1-\frac{x}{b})}{x}$ , x ≠ 0. Encuentra el valor de f en x = 0 para que f se vuelva continua en x = 0.