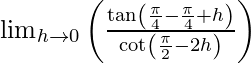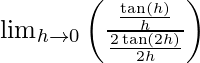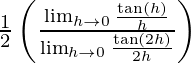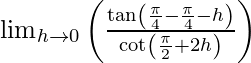Clase 12 Soluciones RD Sharma – Capítulo 9 Continuidad – Ejercicio 9.2

Pregunta 8. Si 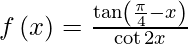$f\left( x \right) = \frac{\tan\left( \frac{\pi}{4} - x \right)}{\cot 2x}$ para x ≠ π/4, encuentre el valor que se le puede asignar a f(x) en x = π/4 para que la función f(x) se vuelva continua en todas partes en [0, π/2].

Solución:

Si x ≠ π/4, tan (π/4 – x) y cot2x son continuas en [0, π/2]. Entonces la función $\frac{\tan \left( \frac{\pi}{4} - x \right)}{\cot 2x}$ es continua para cada x ≠ π/4.

Ahora, supongamos que el punto x = π/4.

Tenemos,

(LHL en x = π/4) = lim _{{x -> π/4-}} f(x)

= lím _{{h -> 0}} f(π/4 – h)

= $\lim_{h \to 0} \left( \frac{\tan\left( \frac{\pi}{4} - \frac{\pi}{4} + h \right)}{\cot\left( \frac{\pi}{2} - 2h \right)} \right)$

= lim _{{h -> 0}} bronceado h/bronceado 2h

= $\lim_{h \to 0} \left( \frac{\frac{\tan \left( h \right)}{h}}{\frac{2 \tan \left( 2h \right)}{2h}} \right)$

= $\frac{1}{2}\left( \frac{\lim_{h \to 0} \frac{\tan \left( h \right)}{h}}{\lim_{h \to 0} \frac{\tan \left( 2h \right)}{2h}} \right)$

= 1/2

(RHL en x = π/4) = lím _{{x -> π/4+}} f(x)

= lím _{{h -> 0}} f(π/4 + h)

= $\lim_{h \to 0} \left( \frac{\tan \left( \frac{\pi}{4} - \frac{\pi}{4} - h \right)}{\cot \left( \frac{\pi}{2} + 2h \right)} \right)$

= lim{h -> 0} tan (-h)/tan (-2h)

= lim _{{h -> 0}} bronceado h/bronceado 2h

= $\lim_{h \to 0} \left( \frac{\frac{\tan \left( h \right)}{h}}{\frac{2 \tan \left( 2h \right)}{2h}} \right)$

= $\frac{1}{2}\left( \frac{\lim_{h \to 0} \frac{\tan \left( h \right)}{h}}{\lim_{h \to 0} \frac{\tan \left( 2h \right)}{2h}} \right)$

= 1/2

Si f(x) es continua en x = π/4 entonces

lím _{{x -> π/4-}} f(x) = lím _{{x -> π/4+}} f(x) = f(π/4)

∴ f(π/4) = 1/2

Por lo tanto, la función será continua en todas partes.

Pregunta 9. Discuta la continuidad de la función 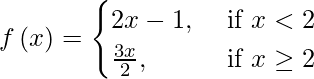$f\left( x \right) = \begin{cases}2x - 1 , & \text { if } x < 2 \\ \frac{3x}{2} , & \text{ if } x \geq 2\end{cases}$ .

Solución:

Cuando x < 2, f(x) siendo una función polinomial es continua.

Cuando x > 2, siendo f(x) un polinomio y una función continua, es continua.

En x = 2, tenemos:

(LHL en x = 2) = lim _{{x -> 2-}} f(x)

= lím _{{h -> 0}} f(2 – h)

= lím _{{h -> 0}} (2(2 – h) – 1)

= 4 – 1

= 3

(RHL en x = 2) = lím _{{x -> 2+}} f(x)

= lím _{{h -> 0}} f(2 + h)

= lím _{{h -> 0}} 3 (h + 2)/2

= 3

Además, f(2) = 3(2)/2 = 3

∴ $\lim_{x \to 2^-} f\left( x \right) = \lim_{x \to 2^+} f\left( x \right) = f\left( 2 \right)$

Entonces, f(x) es continua en x = 2.

Pregunta 10. Discuta la continuidad de f(x) = sen |x|.

Solución:

f es claramente la composición de dos funciones, f = hog, donde g (x) = |x| y h (x) = sen x

Ya que, hog(x) = h(g(x)) = h(|x|) = \sin|x|

g(x)=|x| al ser una función de módulo debe ser continua para todos los números reales.

Supongamos que a sea un número real.

Caso 1:

Si a > 0 entonces g(a) = a

lím _{{x -> c}} (g(x)) = lím _{{x -> c}} (x) = a

Entonces, lim _{{x -> c}} (g(x)) = g(a)

Entonces, g es la continua en todos los puntos, es decir, x > 0

Caso 2:

Si a < 0 entonces g(a) = -a

lím _{{x -> c}} (g(x)) = lím _{{x -> c}} (-x) = -a

Entonces, lim _{{x -> c}} (g(x)) = g(a)

Entonces, g es la continua en todos los puntos x < 0

Caso 3:

Si a = 0 entonces g(a) = g(0) = 0

límite _{{x -> 0 ^– }} (g(x)) = límite _{{x -> 0 ^– }} (-x) = 0

límite _{{x -> 0 ⁺ }} (g(x)) = límite _{{x -> 0 ⁺ }} (x) = 0

Entonces, lím _{{x -> 0 ^– }} (g(x)) = lím _{{x -> 0 ⁺ }} (g(x)) = g(0)

Entonces, g es continuo en el punto x = 0

Entonces, lim _{{x -> c}} (g(x)) = g(a)

Entonces concluimos que h(x) = senx está definida para todo número real.

Consideremos b el número real. Ahora pon x = b + k

Si x->b, entonces k ->0

Entonces, h(b) = sen b

lím _{{x -> b}} (h(x)) = lím _{{x -> b}} sen x

= lim _{{k -> 0}} sen (b + k)

= lim _{{k -> 0}} (senb cos k + cos b sumidero)

= lim _{{k -> 0}} (senb cos k) + lim _{{k -> 0}} (cos b sumidero)

= senb cos 0 + cos b sen 0

= sen b + 0

= sen b

Por lo tanto, lim _{{x -> c}} h(x) = g(c)

Entonces, h es una función continua

Por lo tanto, f(x) = hog(x) = h(g(x)) = h(|x|) = sin|x|

Pregunta 11. Demostrar que 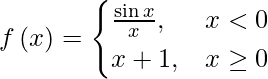$f\left( x \right) = \begin{cases}\frac{\sin x}{x} , & x < 0 \\ x + 1 , & x \geq 0\end{cases}$ es continuo en todas partes.

Solución:

Cuando x < 0, siendo sen x/x el compuesto de dos funciones continuas, es continua.

Cuando x > 0, tenemos que f(x) es una función polinomial continua.

En x = 0:

(LHL en x = 0) = lím _{{x -> 0 ^– }} f(x)

= lím _{{h -> 0}} f(0 – h)

= lím _{{h -> 0}} f(-h)

= lím _{{h -> 0}} (sin (-h)/(-h))

= lim _{{h -> 0}} (sen h/h)

= 1

(LH en x = 0) = lím _{{x -> 0 ⁺ }} f(x)

= lím _{{h -> 0}} f(0 + h)

= lím _{{h -> 0}} f(h)

= límite _{{h -> 0}} (h + 1)

= 1

Además, f(x) = 0 + 1 = 1

Entonces concluimos que lim _{{x -> 0 ^– }} f(x) = lim _{{x -> 0 ⁺ }} f(x) = f(0)

Entonces, f(x) es continua en todas partes.

Pregunta 12. Demuestre que la función g (x) = x − [x] es discontinua en todos los puntos integrales. Aquí [x] denota la función entera más grande.

Solución:

g está definida en todos los puntos integrales. Sea n un número entero. Después,

g(n) = norte − [n]

= norte – norte

= 0

En x = n, tenemos:

LHL = lím _{{x -> n ^– }} g(x) = lím _{{x->n ^– }} (x – [x])

= lím _{{x->n ^– }} (x) – lím _{_ {x->n ^– }} [x]

= norte – (n – 1)

= 1

RHL = lím _{{x->n ⁺ }} g(x) = lím _{{x->n ⁺ }} (x – [x])

= lím _{{x-> n ⁺ }} (x) – lím _{{x->n ⁺ }} [x]

= norte – norte

= 0

Entonces concluimos que lim _{{x -> 0 ^– }} f( x ) ≠ lim _{{x -> 0 ⁺ }} f(x)

Entonces, g es discontinua en todos los puntos integrales.

Pregunta 13. Discutir la continuidad de las siguientes funciones:

(i) f(x) = sen x + cos x

(ii) f(x) = sen x − cos x

(iii) f(x) = sen x cos x

Solución:

Sabemos que si g y h son dos funciones continuas, entonces g + h, g − h y goh también son continuas.

Sea g (x) = sen x, definido para todo número real.

Sea a un número real. Ponga x = a + h

Si x → a, entonces h → 0 g(a)=sen a.

lím _{x->a} g(x) = lím _{x->a} sina

= lim _{h->0} sin (a+h)

= lim _{h->0} [sen a cos h + cos a sen h]

= lim _{h->0} (sen a cos h )+lim _{h->0} (cos a sen h)

= sen a cos 0 + cos a sen 0

= pecado (a + 0)

= pecado un

∴ lím _{x->c} g(x) = g(c)

De manera similar, cos x puede demostrarse como una función continua.

Entonces concluimos que

(i) f (x) = g (x) + h (x) = sen x + cos x es una función continua.

(ii) f (x) = g (x) − h (x) = sen x − cos x es una función continua.

(iii) f (x) = g (x) h (x) = sen x cos x es una función continua.

Pregunta 14. Demuestre que f (x) = cos x ² es una función continua.

Solución:

f puede escribirse como la composición de dos funciones como f = goh, donde g (x) = cos x y h (x) = x ²

∵ (goh)(x) = g(h (x)) = g(x ² ) = cos(x ² ) = f(x)

Sea c un número real.

Entonces, g(c) = cos c

Si x-> c , entonces h->0 y lim _{x->c} g(x)

= lím _{x->c} cos c

= porque c

∴ lím _{x->c} g(x) = g(c)

Entonces, g(x) = cos x es una función continua.

Ahora, h(x) = ^x2

Sea k un número real, entonces h(k) = k ²

lím _x->h (x) = lím _{x->k} x ² = k ²

∴ lím _{x->k} h(x) = h(k)

Entonces, h es una función continua.

Entonces, f(x) siendo un compuesto de dos funciones continuas es una función continua.

Pregunta 15. Demuestre que f (x) = |cos x| es una función continua.

Solución:

f es la composición de dos funciones como, f = goh, donde g(x) = |x| y h(x) = cos x

(goh)(x) = g(h(x)) = g(cos x) = |cos x| = f(x)

Claramente, g(x) siendo una función de módulo sería continua en todos los puntos.

Ahora, h (x) = cos x. Sabemos que h (x) = cos x está definido para todo número real.

Sea c un número real.

Ponga x = c + h.

Si x → c, entonces h → 0.

⇒ h(c) = cos c

Entonces, h (x) = cos x es una función continua.

Por lo tanto, f(x) siendo un compuesto de dos funciones continuas es una función continua.

Pregunta 16. Encuentra todos los puntos de discontinuidad de f definidos por f (x) = |x| − |x + 1|.

Solución:

f es la composición de dos funciones como f(x) = g(x) – h(x), donde g(x) = |x| y h(x) = |x + 1|.

Sea c un número real.

Caso I: Si c < 0 , entonces g(c) = -c y lim _{x->c} g(x) = lim _{x->c} = -c

∴ lím _{x->c} g(x) = g(c)

Entonces, g es continua en todos los puntos x < 0.

Caso II: Si c < 0 , entonces g(c) = -c y lim _(x->c) g(x) = lim _(x->c) (-x) = -c

∴ lím _(x->c) g(x) = g(c)

Entonces, g es continua en todos los puntos x > 0.

Caso III: si c = 0 , entonces g (c) = g(0) = 0

lím _{x->0-} g(x) = lím _{x->0-} (- x) = 0

lím _{x->0+} g(x) = lím _{x->0+} (x) = 0

∴ lím _{x->0+} g(x) = lím _{x->0+} (x) = g(0)

Entonces, g es continua en todas partes.

Claramente, h está definida para todo número real. Sea c un número real.

Caso I: si c < – 1, entonces h (c) = – (c + 1)

lím _{x->c} h (x) = lím _{x->c} [-(x + 1)]

= -(c + 1)

∴ lím _{{x-> c}} h (x) = h (c)

Por lo tanto, f siendo un compuesto de dos funciones continuas es una función continua.

Pregunta 17. ¿Determinar si 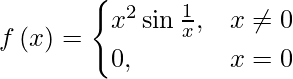$f\left( x \right) = \begin{cases}x^2 \sin\frac{1}{x} , & x \neq 0 \\ 0 , & x = 0\end{cases}$ es una función continua?

Solución:

Supongamos que c es un número real.

Caso I: Si c ≠ 0 , entonces f(c)= c ² sin (1/c)

lím _{x->c} f(x) = lím _{x->c} (x ² sen 1/x)

= (lím _{x->c} x ² ) (lím _{x->c} sen 1/x)

= c ² sen (1/c)

lím _{x->c} f(x) = f(c)

Entonces, f es continua en todos los puntos tal que x ≠ 0

Caso II: Si c = 0 entonces f(0) = 0

lím _{{x -> 0 ^– }} f(x) = lím _{{x -> 0 ^– }} (x ² sen 1/x) = lím _{{x -> 0}} (x ² sen 1/x)

Entonces, -1 ≤ sen 1/x ≤ 1, x ≠ 0

-x ² ≤ x ² sen 1/x ≤ x ²

lím _{{x -> 0}} (-x ² ) ≤ lím _{{x -> 0}} (x ² sen 1/x) ≤ lím _{{x -> 0}} x ²

0 ≤ lím _{{x -> 0}} (x ² sen 1/x) ≤ 0

lím _{{x -> 0}} (x ² sen 1/x) = 0

límite _{{x -> 0 ^– }} f(x) = 0

De manera similar, lim _{{x -> 0 ⁺ }} f(x) = lim _{{x -> 0 ⁺ }} (x ² sen 1/x) = lim _{{x -> 0}} (x ² sen 1/x) = 0

Por lo tanto, f es una función continua.

Pregunta 18. Dada la función 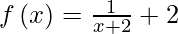$f\left( x \right) = \frac{1}{x + 2}+2$ . Encuentra los puntos de discontinuidad de la función f(f(x)).

Solución:

Aquí, $f[f(x)]=\frac{1}{\frac{1}{x+2}+2}=\frac{x+2}{2x+5}$

Observamos que f(f( x )) no está definida en x + 2 = 0 y 2x + 5 = 0.

Si x + 2 = 0, entonces x = – 2 y si 2x + 5 = 0, entonces x = -5/2

Por tanto, la función es discontinua en x = -5/2 y – 2.

Pregunta 19. Encuentra todos los puntos de discontinuidad de la función f(t) = 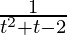$\frac{1}{t^2 + t - 2}$ , donde t = 1/(x – 1).

Solución:

Aquí, $f\left( t \right) = \frac{1}{t^2 + t - 2}$

Ahora, sea u = 1/(x – 1)

Por lo tanto f( u ) = $\frac{1}{u^2 + 2u - u - 2}$

= $\frac{1}{\left( u + 2 \right)\left( u - 1 \right)}$

Entonces, f (u ) no está definida en u = -2 y u = 1.

Si u = – 2, entonces -2 = 1/(x – 1)

⇒ 2x = 1

⇒ x = 1/2

Si u = 1, entonces 1 = 1/(x – 1)

⇒ x = 2

Por lo tanto, la función es discontinua en x = 1/2 , 2.

Publicación traducida automáticamente

Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones RD Sharma – Capítulo 9 Continuidad – Ejercicio 9.2 | conjunto 2

Pregunta 8. Si $f\left( x \right) = \frac{\tan\left( \frac{\pi}{4} - x \right)}{\cot 2x}$ para x ≠ π/4, encuentre el valor que se le puede asignar a f(x) en x = π/4 para que la función f(x) se vuelva continua en todas partes en [0, π/2].

Pregunta 9. Discuta la continuidad de la función $f\left( x \right) = \begin{cases}2x - 1 , & \text { if } x < 2 \\ \frac{3x}{2} , & \text{ if } x \geq 2\end{cases}$ .

Pregunta 10. Discuta la continuidad de f(x) = sen |x|.

Pregunta 11. Demostrar que $f\left( x \right) = \begin{cases}\frac{\sin x}{x} , & x < 0 \\ x + 1 , & x \geq 0\end{cases}$ es continuo en todas partes.

Pregunta 12. Demuestre que la función g (x) = x − [x] es discontinua en todos los puntos integrales. Aquí [x] denota la función entera más grande.

Pregunta 13. Discutir la continuidad de las siguientes funciones:

(i) f(x) = sen x + cos x

(ii) f(x) = sen x − cos x

(iii) f(x) = sen x cos x

Pregunta 14. Demuestre que f (x) = cos x ² es una función continua.

Pregunta 15. Demuestre que f (x) = |cos x| es una función continua.

Pregunta 16. Encuentra todos los puntos de discontinuidad de f definidos por f (x) = |x| − |x + 1|.

Pregunta 17. ¿Determinar si $f\left( x \right) = \begin{cases}x^2 \sin\frac{1}{x} , & x \neq 0 \\ 0 , & x = 0\end{cases}$ es una función continua?

Pregunta 18. Dada la función $f\left( x \right) = \frac{1}{x + 2}+2$ . Encuentra los puntos de discontinuidad de la función f(f(x)).

Pregunta 19. Encuentra todos los puntos de discontinuidad de la función f(t) = $\frac{1}{t^2 + t - 2}$ , donde t = 1/(x – 1).

Deja una respuesta Cancelar la respuesta

Pregunta 8. Si para x ≠ π/4, encuentre el valor que se le puede asignar a f(x) en x = π/4 para que la función f(x) se vuelva continua en todas partes en [0, π/2].

Pregunta 9. Discuta la continuidad de la función .

Pregunta 10. Discuta la continuidad de f(x) = sen |x|.

Pregunta 11. Demostrar que es continuo en todas partes.

Pregunta 12. Demuestre que la función g (x) = x − [x] es discontinua en todos los puntos integrales. Aquí [x] denota la función entera más grande.

Pregunta 13. Discutir la continuidad de las siguientes funciones:

(i) f(x) = sen x + cos x

(ii) f(x) = sen x − cos x

(iii) f(x) = sen x cos x

Pregunta 14. Demuestre que f (x) = cos x 2 es una función continua.

Pregunta 15. Demuestre que f (x) = |cos x| es una función continua.

Pregunta 16. Encuentra todos los puntos de discontinuidad de f definidos por f (x) = |x| − |x + 1|.

Pregunta 17. ¿Determinar si es una función continua?

Pregunta 18. Dada la función . Encuentra los puntos de discontinuidad de la función f(f(x)).

Pregunta 19. Encuentra todos los puntos de discontinuidad de la función f(t) = , donde t = 1/(x – 1).

Deja una respuesta Cancelar la respuesta

Pregunta 8. Si $f\left( x \right) = \frac{\tan\left( \frac{\pi}{4} - x \right)}{\cot 2x}$ para x ≠ π/4, encuentre el valor que se le puede asignar a f(x) en x = π/4 para que la función f(x) se vuelva continua en todas partes en [0, π/2].

Pregunta 9. Discuta la continuidad de la función $f\left( x \right) = \begin{cases}2x - 1 , & \text { if } x < 2 \\ \frac{3x}{2} , & \text{ if } x \geq 2\end{cases}$ .

Pregunta 11. Demostrar que $f\left( x \right) = \begin{cases}\frac{\sin x}{x} , & x < 0 \\ x + 1 , & x \geq 0\end{cases}$ es continuo en todas partes.

Pregunta 14. Demuestre que f (x) = cos x ² es una función continua.

Pregunta 17. ¿Determinar si $f\left( x \right) = \begin{cases}x^2 \sin\frac{1}{x} , & x \neq 0 \\ 0 , & x = 0\end{cases}$ es una función continua?

Pregunta 18. Dada la función $f\left( x \right) = \frac{1}{x + 2}+2$ . Encuentra los puntos de discontinuidad de la función f(f(x)).

Pregunta 19. Encuentra todos los puntos de discontinuidad de la función f(t) = $\frac{1}{t^2 + t - 2}$ , donde t = 1/(x – 1).