Pregunta 1. Demuestra que la función 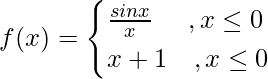 es continua en todas partes.
es continua en todas partes.
Solución:
Sabemos que sen x/x es continuo en todas partes ya que es la función compuesta de las funciones sen x y x que son continuas.
Cuando x > 0, tenemos f(x) = x + 1.
Dado que
Ahora, (LHL en x = 0) = lim {x ⇢ 0 – } f(x)
= límite {h ⇢ 0} f(0 – h)
= lím {h ⇢ 0} f(-h)
= lím{h ⇢ 0} (sen (-h)/(-h))
= lím {h ⇢ 0} (sen h/ h)
= 1
(RHL en x = 0) = lím {x ⇢ 0+} f(x)
= límite {h ⇢ 0} f(0 + h)
= límite {h ⇢ 0} f(h)
= límite {h ⇢ 0} (h + 1)
= 1
y f(0) = 0 + 1 = 1.
Observamos que: lim {x ⇢ 0 – } f(x) = lim {x ⇢ 0 + } f(x) = f(0).
Por lo tanto, f(x) es continua en todas partes.
Pregunta 2. Discuta la continuidad de la función 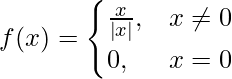 .
.
Solución:
Tenemos,
Ahora: (LHL en x = 0) = lim {x ⇢ 0 – } f(x)
= límite {h ⇢ 0} f(0 – h)
= lím {h ⇢ 0} f(–h)
= límite {h⇢ 0} (–1)
= –1
(RHL en x = 0) = lím {x ⇢ 0 + } f(x)
= límite {h ⇢ 0} f(0 + h)
= límite {h ⇢ 0} (1)
= 1
Observamos que, lim {x ⇢ 0 – } f(x) ≠ lim {x ⇢ 0 + } f(x).
Por lo tanto, f(x) es discontinua en x = 0.
Pregunta 3. Encuentra los puntos de discontinuidad, si los hay, de las siguientes funciones:
(i) 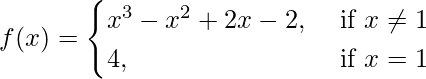
Solución:
Dado que una función polinomial es continua en todas partes.
En x = 1, tenemos
(LHL en x = 1) = lím {x ⇢ 1 – } f(x)
= límite {h ⇢ 0} f(1 – h)
= límite {h ⇢ 0} ((1 – h) 3 – (1 – h ) 2 + 2(1 – h) – 2)
= 1 – 1 + 2 – 2
= 0
(RHL en x = 1) = lím {x ⇢ 1 + } f(x)
= límite {h ⇢ 0} f(1 + h)
= lím{h ⇢ 0} ((1 + h) 3 – (1 + h ) 2 + 2(1 + h) – 2)
= 1 – 1 + 2 – 2
= 0
Además, f(1) = 4.
Observamos que, lim {x ⇢ 0 – } f(x) = lim {x ⇢ 0 + } f(x) ≠ f(1).
Por lo tanto, f(x) es discontinua solo en x = 1.
(ii) 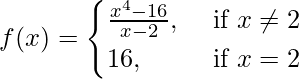
Solución:
Cuando x ≠ 2 entonces
f(x) =
=
=
= (x 2 + 4)(x + 2)
Dado que una función polinomial es continua en todas partes, (x 2 + 4) y (x + 2) son continuas en todas partes.
Entonces, la función producto (x 2 + 4)(x + 2) es continua.
Por tanto, f(x) es continua en todo x ≠ 2 .
Observamos que lim {x->2-} f(x) = lim {x->2+} f(x) = f(2)
Por lo tanto, f(x) es discontinua solo en x = 2.
(iii) 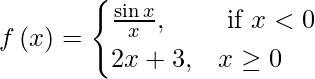
Solución:
Cuando x < 0, entonces f(x) = sen x/ x.
Como sen x y la función identidad x son continuas en todas partes, la función cociente sen x/x es continua en cada x < 0.
Para x > 0, f(x) se convierte en una función polinomial. Por lo tanto, f(x) es continua en cada x > 0.
Tenemos: (LHL en x = 0) = lim {x->0-} f(x)
= lím {h -> 0} f(0 – h)
= lím {h -> 0} f (-h)
= lím {h -> 0} (sen(-h)/(-h))
= lim {h -> 0} (sen h/h)
= 1
(RHL en x = 0) = lim _{x -> 0+} f(x)
= lím {h -> 0} f(0 + h)
= lím {h -> 0} f(h)
= límite {h -> 0} (2h + 3)
= 3
Observamos que lim {x -> 0-} f(x) ≠ lim {x -> 0+} f(x)
Por lo tanto, f(x) es discontinua solo en x = 0.
(iv) 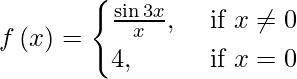
Solución:
En x ≠ 0, entonces f(x) = sen 3x/ x.
Dado que las funciones sen 3x y x son continuas en todas partes. Entonces, la función cociente sen 3x/x es continua en cada x ≠ 0.
Tenemos: (LHL en x = 0) = lim {x -> 0+} f(x)
= lím {h -> 0} f(0 + h)
= lím {h -> 0} f(h)
= lím {h -> 0} (sen 3h/h)
= lím {h -> 0} 3 (sen h/h) = 3
(RHL en x = 0) = lím {x -> 0+} f(x)
= lím {h -> 0} f(0 + h)
= lím {h -> 0} f(h)
= lím {h -> 0} (sen 3h/h)
= lim {h -> 0} 3 (sen 3h/h)
= 3
Además, f(0) = 4.
Observamos que lim {x -> 0-} f(x) = lim {x -> 0+} f(x) = f(0)
Por lo tanto, f(x) es discontinua solo en x = 0.
(v) 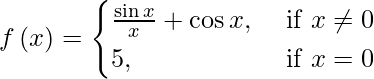
Solución:
Cuando x ≠ 0, entonces f(x) = sen x/ x + cos x.
Sabemos que tanto sen x como cos x son continuos en todas partes. Por lo tanto, la función dada es continua en cada x ≠ 0.
Consideremos el punto x = 0.
Dado:
Tenemos: (LHL en x = 0) = lim {x -> 0-} f(x)
= lím {h -> 0} f(0 – h)
= lím {h -> 0} f(-h)
= lím {h -> 0} [(sen (-h)/(-h)) + cos (-h)]
= lím {h -> 0} sin(-h)/(-h) + lím {h -> 0} cos(-h)
= 1 + 1
= 2
(RHL en x = 0) = lím {x -> 0+} f(x)
= lím {h -> 0} f(0 + h)
= lím {h -> 0} f(h)
= lím {h -> 0} [(sen h/h) + cos (-h)]
= lím {h -> 0} sen h/h + lím {h -> 0} cos(-h)
= 1 + 1
= 2
Además, f(0) = 5.
Observamos que lim {x -> 0-} f(x) = lim {x -> 0^+} f(x) ≠ f(0)
Por lo tanto, f(x) es discontinua solo en x = 0.
(vi) 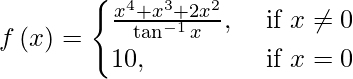
Solución:
Cuando x ≠ 0, entonces
x 4 + x 3 + 2x 2 siendo una función polinomial es continua en todas partes.
Además, tan -1 x es continuo en todas partes.
Consideremos el punto x = 0.
Tenemos:
(LHL en x = 0) = lim {x -> 0-} f(x)
= lím {h -> 0} f(0 – h)
= lím {h -> 0} f(-h)
=
=
= 0
(RHL en x = 0) = lím {x -> 0+} f(x)
= lím {h -> 0} f(0 + h)
= lím {h -> 0} f(h)
=
=
= 0
Además, f(0) = 10.
Observamos que lim {x -> 0-} f(x) = lim {x -> 0 + } f(x) ≠ f(0)
Por lo tanto, f(x) es discontinua solo en x = 0.
(vii) 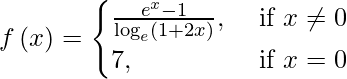
Solución:
Tenemos,
=
=
= 1/2
Se da que f(0) = 7.
Observamos que lim {x -> 0} f(x) ≠ f(0)
Por lo tanto, f(x) es discontinua solo en x = 0.
(viii) 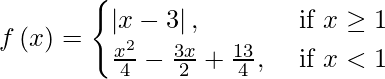
Solución:
En x > 1, siendo f(x) una función de módulo, es continua para cada x > 1.
Cuando x < 1, entonces f( x ) siendo un compuesto de funciones polinómicas y continuas sería continua.
En x = 1, tenemos
(LHL en x = 1) = lim {x -> 1-} f(x)
= lím {h -> 0} f(1 – h)
=
![Rendered by QuickLaTeX.com \lim_{h\to0} \left[ \frac{\left( 1 - h \right)^2}{4} - \frac{3\left( 1 - h \right)}{2} + \frac{13}{4} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8cb1facd7269b05ce0c200cab77dbac9_l3.png)
= 1/4 – 3/2 + 13/4
= 2
(LH en x = 1) = lím {x -> 1+} f(x)
= lím {h -> 0} f(1 + h)
= lím {h -> 0} |1 + h – 3|
= |-2|
= 2
También f(1) = |1 – 3| = |- 2| = 2
Observamos que, lim {x -> 1-} f(x) = lim {x -> 1+} f(x) = f(1)
Por lo tanto, la función dada es continua en todas partes.
(ix) 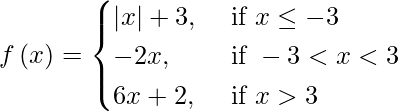
Solución:
f(x) siendo una función de módulo es continua para cada x ≤ – 3.
At – 3 < x < 3 f(x) siendo una función polinomial es continua.
En x > 3, f(x) siendo una función polinomial es continua.
En x = 3,
Tenemos: (LHL en x = 3) = lim {x -> 3-} f(x)
= lím {h -> 0} f(3 – h)
= lím {h -> 0} -2(3 – h)
= -6
(RHL en x = 3) = lim {x -> 3+} f(x)
= lím {h -> 0} f(3 + h)
= lím {h -> 0} 6(3 + h) + 2
= 20
Observamos que lim {x -> 3-} f(x) ≠ lim {x -> 3+} f(x)
Por lo tanto, f(x) es discontinua solo en x = 3.
(X) 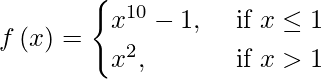
Solución:
De acuerdo a la pregunta se da que la función f está definida en todos los puntos de la recta real.
Consideremos c como un punto sobre la recta real.
Caso I: Si c< 1, entonces f(c) = c 10 −1 y
lím {x-> c} f(x) = lím {x->c} (x 10 – 1)
= c 10 −1.
∴ lím {x->c} f(x) = f(c)
Por tanto, f es continua para todo x < 1.
Caso II: Si c = 1, entonces el límite izquierdo de f en x = 1.
El límite derecho de f en x = 1 es, lim (x->1) f(x) = lim (x->1) (x 2 ) = 1 2 = 1
Entonces concluimos que los límites izquierdo y derecho de f en x = 1 no coinciden. Entonces, f no es continua en x = 1.
Caso III: Si c>1, entonces f(c) = c 2
lím (x->c) f(x) = lím (x->c) f(c) = c 2
∴ lím (x->c) f(x) = f(c)
Por lo tanto, f(x) es discontinua solo en x = 1.
(xi) 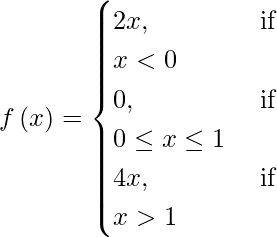
Solución:
Consideremos a como un punto sobre la recta real.
Caso I: si a < 0, entonces f(c) = 2a.
lím {x->a} (a) = 2a.
∴ lím {N -> 0} f(x) = f(a)
Entonces, f es continua en todos los puntos tal que x < 0.
Caso II: Si 0 < a < 1 entonces f(x) y lim {x->a} f(x)=lim {x->a} (0)=0 .
∴ lím {x->a} f(x)=f(a)
Entonces, f es continua en todos los puntos del intervalo (0, 1).
Caso III: Si a =1 entonces f(a) = f(1) = 0.
El límite izquierdo de f en x = 1 es,
límite {x->1} f(x) = límite {x->1} f(1)
El límite derecho de f en x = 1 es,
lím {x->1} f(x) = lím {x->1} (4x) = 4(1) = 4
Entonces concluimos que LHL ≠ RHL. Por tanto, f no es continua en x = 1.
Caso IV: Si a > 1, entonces f(a) = 4a y lim {x->a} f(4x) = 4a .
∴ lím {x->a} f(x) = f(a)
Entonces, f(x) es discontinua solo en x = 1.
(xii) 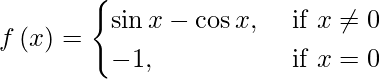
Solución:
Es evidente que f está definida en todos los puntos de la recta real. Sea p un número real.
Caso I: si p ≠ 0 , entonces f (p) = sen p – cos p
lim {x → p} f(x) = lim {x→p} ( sen x – cos x ) = sen p – cos p
∴ lím {x →p} f(x) = f(p)
Por tanto, f es continua en todos los puntos x, tal que x ≠ 0.
Caso II: si p = 0 , entonces f (0) = – 1.
lím {x →0-} f(x) = lím {x →0^-} (sen x – cos x) = sen 0 – cos 0 = 0 – 1 = -1
lím {x →0+} f(x) = lím {x →0} (sen x – cos x) = sen 0 – cos 0 = 0 – 1 = -1
Observamos que: lim {x →0-} f (x) = lim {x →0+} f (x)= f(0)
Por lo tanto, f es una función continua en todas partes.
(xii) 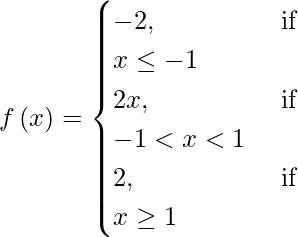
Solución:
La función dada está definida en todos los puntos de la recta real. Consideremos a como un punto sobre la recta real.
Caso I: Si a < -1 entonces f(a)= -2 y lim {x->a} (x) = lim {x->a} (-2) = -2
∴ lím {x->a} f(x) = f(a)
f es continua para todo x < −1.
Caso II: Si a =1 entonces f(a) = f(-1) = -2
LHL = lím {x->-1} f(x) = lím {x->-1} f(-2) = -2
RHL = lím {x->-1} f(x) = lím {x->-1} f(2x) = 2(-1) = -2
Observamos que lim {x->-1} f(x) = f(-1)
Por lo tanto, f es continua en x = −1.
Caso III: si -1 < a < 1, entonces f(a) = 2a
lím {x->a} f(x) = lím {x->a} f(2x) = 2a
∴ lím {x->a} f(x) = f(a)
Por lo tanto, f es continua en todos los puntos del intervalo (−1, 1).
Caso IV: si a = 1, entonces f(c) = f(1) = 2(1) = 2.
LHL = lím {x->1} f(x) = lím {x->1} 2 = 2
RHL = lím {x->1} f(x) = lím {x->1} 2 = 2
Observamos que: lim {x->1} f(x) = lim {x->1} f(c)
Por lo tanto, f es continua en x = 2.
Por lo tanto, f es una función continua en todas partes.
Pregunta 4. A continuación, determine el valor de la constante involucrada en la definición para que la función dada sea continua:
(i) 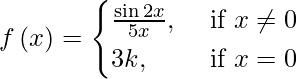
Solución:
Si f( x ) es continua en x = 0, entonces
⇒ lím{x -> 0} f(x) = f(0)
⇒ lím {x -> 0} sen 2x/5x = f(0)
⇒ lím {x -> 0} 2 sen 2x/10x = f(0)
⇒ 2/5 lím {x -> 0} sen 2x/2x = f(0)
⇒ k = 2/15
(ii) 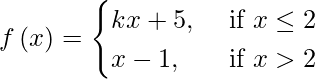
Solución:
Si f(x) es continua en x = 2, entonces
límite {x -> 2-} f(x) = límite {x -> 2+} f(x)
⇒ límite {h -> 0} (k (2 – h) + 5) = límite {h -> 0} (2 + h -1)
⇒ límite {h -> 0} f(2 – h) = límite {h -> 0} f(2 + h)
⇒ 2k + 5 = 1
⇒ 2k = – 4
⇒ k = – 2
(iii) 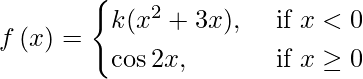
Solución:
Si f(x) es continua en x = 0, entonces
límite {x -> 0-} f(x) = límite {x -> 0+} f(x)
⇒ límite {h -> 0} f(-h) = límite {h -> 0} f(h)
⇒
⇒ 0 = 1, lo cual no es posible
Por lo tanto, la función dada no es continua para ningún valor de k.
(iv) 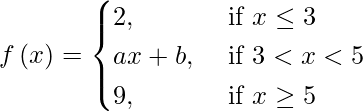
Solución:
Si f(x) es continua en x = 3 y 5, entonces
límite {x -> 3-} f(x) = límite {x -> 3+} f(x)
y lím {x -> 5-} f(x) = lím {x -> 5+} f(x)
⇒ límite {h -> 0} f(3 – h) = límite {h -> 0} f(3 + h)
y lim {h -> 0} f(5 – h) = lim {h -> 0} f(5 + h)
⇒ 2 = 3a + b y 5a + b = 9
⇒ 2 = 3a + b y 5a + b = 9
⇒ a = 7/2 yb = -17/2.
(v) 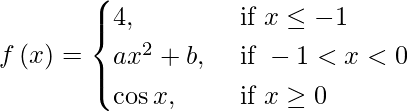
Solución:
Si f(x) es continua en x = −1 y 0, entonces
lím {x -> -1-} f(x) = lím {x -> – 1+} f(x) y lím {x -> 0-} f(x) = lím {x -> 0+} f (X)
⇒ lím {h -> 0} f(-1 – h) = lím {h -> 0} f(-1 + h) y lím {h -> 0} f(-h) = lím {h -> 0 } f(h)
⇒ límite {h -> 0} (4) = límite {h -> 0} (a (-1 + h) 2 + b)
También,
⇒ 4 = a + b y b = 1
⇒ a = 3 y b = 1.
(vi) 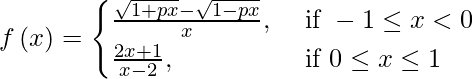
Solución:
Si f(x) es continua en x = 0, entonces
⇒
⇒
⇒
⇒
⇒
⇒
⇒ 2p/2 = -1/2
⇒ p = -1/2.
(vii) 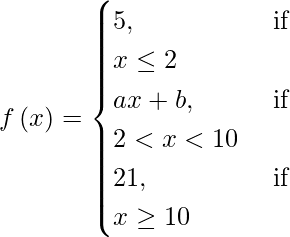
Solución:
Si f(x) es continua en x = 2 y x = 10, entonces
lím {x -> 2-} f(x) = lím {x -> 2+} f(x) y lím {x -> {10} – } f(x) = lím {x -> {10}+ } f(x)
⇒ lím {h -> 0} f(2 – h) = lím {h -> 0} f(2 + h) y lím {h -> 0} f(10 – h) = lím {h -> 0} f(10 + h)
⇒ límite {h -> 0} (5) = límite {h -> 0} (a (2 + h) + b)
Y lim {h -> 0} a (10 – h) + b = lim {h -> 0} (21)
Al resolver ecuaciones, obtenemos,
⇒ a = 2 y b = 1.
(viii) 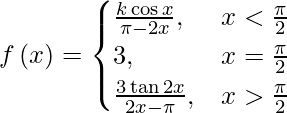
Solución:
Si f(x) es continua en x = π/2, entonces
lím {x -> π/2-} f(x) = f(π/2)
⇒ lím {h -> 0} f(π/2 – h) = f(π/2)
⇒ lím {h -> 0} f(π/2 – h) = 3
⇒
⇒
⇒ lím {h -> 0} (k sen h/2h) = 3
⇒ k/2 lím {h -> 0} sen h/h =3
⇒ k/2 = 3
⇒ k = 6
Pregunta 5. La función  es continua en (0, ∞), luego encuentre los valores más adecuados de a y b.
es continua en (0, ∞), luego encuentre los valores más adecuados de a y b.
Solución:
Dado que f es continua en ( 0, ∞ ).
Entonces, f es continua en x = 1 y x = √2.
En x = 1, tenemos lim {x -> 1-} f(x)
= lím {h -> 0} f(1 – h)
= lím {h -> 0} [(1 – h) 2 /a]
= 1/a
En x = √2, tenemos
lím {x -> √2-} f(x) = lím {h -> 0} f(√2 + h)
= lím {h -> 0} (a)
= un
f es continua en x = 1 y √2.
⇒ 1/a = a y b 2 – 2b = a
⇒ a 2 = 1 y b 2 – 2b = a
⇒ a = ±1 y b 2 – 2b = a . . . (1)
Si a = 1, entonces b 2 – 2b = 1
⇒ segundo 2 – 2b – 1 = 0
⇒ segundo =
= 1 ± √2
Si a = −1, entonces b 2 – 2b = – 1
⇒ segundo 2 – 2b + 1 = 0
⇒ segundo = 1
Por tanto, a = −1, b = 1 oa = 1, b = √2.son los valores más adecuados de a y b.
Pregunta 6. Encuentra los valores de ayb para que la función f(x) definida por 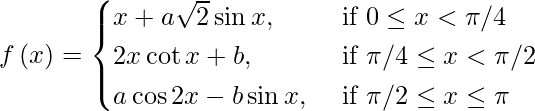 se vuelva continua en [0, π].
se vuelva continua en [0, π].
Solución:
f es continua en x = π.
En x = π/4, tenemos
lím {x -> π/4-} f(x) = lím {h -> 0} f(π/4 – h)
= lím{h -> 0} [(π/4 – h) + √2a sen (π/4 – h)]
= π/4 + √2a sen π/4
= π/4 + a
= lim {h -> 0} [2 (π/4 + h) cot (π/4 + h) + b]
= [2 π/4 cuna π/4 + b]
= π/2 + segundo
⇒ – segundo – un = segundo y π/4 + un = π/2 + segundo
⇒ a = π/6 y b = -π/12
Pregunta 7. La función f(x) se define como sigue: 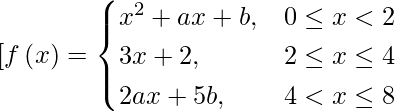 . Si f es continua en [0, 8], encuentre los valores de a y b.
. Si f es continua en [0, 8], encuentre los valores de a y b.
Solución:
Dado que f es continua en [0, 8].
Entonces, f es continua en x = 2 y x = 4
En x = 2,
límite {x -> 2-} f(x) = límite {h -> 0} f(2 – h)
= lím {h -> 0} (2 – h) 2 + a(2 – h) + b
= 4 + 2a + b
límite {x -> 2+} f(x) = límite {h -> 0} f(2 + h)
= límite {h -> 0} [3(2 + h) + h]
= 8
En x = 4,
límite {x -> 4-} f(x) = límite {h -> 0} f(4 – h)
= lim_{h -> 0} [3(4 – h) + 2]
= 14
límite {x -> 4+} f(x) = límite {h -> 0} f(4 + h)
= límite {h -> 0} [2a(4 + h) + 5b]
= 8a + 5b
Entonces, f es continua en x = 2 y x = 4.
límite {x -> 2-} f(x) = límite {x -> 2+} f(x)
y, lím {x -> 4-} f(x) = lím {x -> 4+} f(x)
⇒ 4 + 2a + b = 8 y 8a + 5b = 14
⇒ 2a + b = 4 y 8a + 5b = 14
Al resolver obtenemos
a = 3 y b = -2
Publicación traducida automáticamente
Artículo escrito por prabhjotkushparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
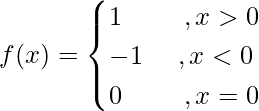
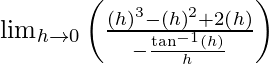
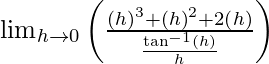
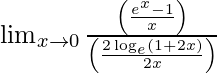
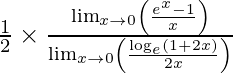
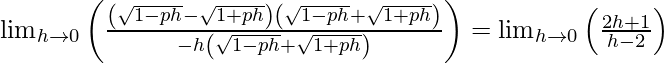
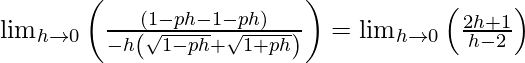
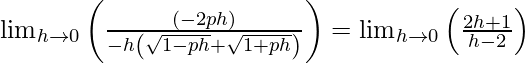
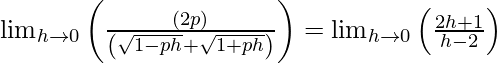
![Rendered by QuickLaTeX.com \lim_{h \to 0} \left[ \frac{k \cos \left( \frac{\pi}{2} - h \right)}{\pi - 2\left( \frac{\pi}{2} - h \right)} \right] = 3](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b473429557488541c8a5594f1623c241_l3.png)
![Rendered by QuickLaTeX.com \lim_{x \to \sqrt{2}^+} f\left( x \right) = \lim_{h \to 0} f\left( \sqrt{2} + h \right) = \lim_{h \to 0} \left[ \frac{2 b^2 - 4b}{\left( \sqrt{2} + h \right)^2} \right] = \frac{2 b^2 - 4b}{2} = b^2 - 2b](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a87ad24717e1664aed6493de772b5d24_l3.png)