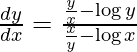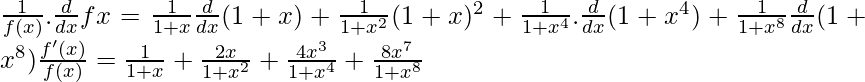Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 5 Continuidad y diferenciabilidad – Ejercicio 5.5

Capítulo 5 Continuidad y Diferenciabilidad – Ejercicio 5.5 | Serie 1

Pregunta 11. Deriva la función con respecto a x.

(x cos x) ^x + (x sen x) ^1/x

Solución:

Dado: (x cos x) ^x + (x sen x) ^1/x

Consideremos y = u + v

Donde, u = (x cos x) ^x y v = (x sen x) ^1/x

Entonces, dy/dx = du/dx + dv/dx ………(1)

Primero tomamos u = (x cos x) ^x

Al tomar el registro en ambos lados, obtenemos

log u = log(x cos x) ^x

log u = xlog(x cos x)

Ahora, al derivar wrt x, obtenemos

$\frac{1}{u}\frac{du}{dx}=x\frac{d}{dx}(\log x+\log(\cos x))+\log x+\log \cos x$

$\frac{1}{u}\frac{du}{dx}=x(\frac{1}{x}+\frac{1}{\cos x}\frac{d}{dx}\cos x)+\log x+\log\cos x$

$\frac{du}{dx}=u(x(\frac{1}{x}+\frac{-\sin x}{\cos x})+\log x+\log(\cos x))$

$\frac{du}{dx}=(x\cos x)^x(1-x\tan x+\log x+\log(\cos x))$ ………(2)

Ahora tomamos u =(x sen x) ^1/x

Al tomar el registro en ambos lados, obtenemos

log v = log (x sen x) ^1/x

log v = 1/x log (x sen x)

log v = 1/x(log x + log sen x)

Ahora, al derivar wrt x, obtenemos

$\frac{1}{v}\frac{dv}{dx}=\frac{1}{x}\frac{d}{dx}(\log x+\log(\sin x)+\frac{d}{dx}(\frac{1}{x}).(\log x+\log(\sin x)))$

$\frac{1}{v}.\frac{dv}{dx}=\frac{1}{x}(\frac{1}{x}+\frac{1}{\sin x}.\frac{d}{dx}\sin x)+(\frac{-1}{x^2})(\log x+\log(\sin x))$

$\frac{dv}{dx}=v(\frac{1}{x}(\frac{1}{x}+\frac{\cos x}{\sin x})\frac{-1}{x^2}(\log x+\log(\sin x)))$

$\frac{dv}{dx}=(x\sin x)^{1/2}.[(\frac{1}{x^2}+\frac{\cot x}{x})-\frac{\log x}{x^2}-\frac{\log(\sin x)}{x^2}]$ ………(3)

Ahora ponga todos los valores de eq(2) y (3) en eq(1)

$\frac{dy}{dx}=(x\cos)^x(1-x\tan x+\log x+\log(\cos x))+(x\sin x)^{\frac{1}{x}}.[\frac{xcotx+1-log(xsinx)}{x^2}]$

Encuentre dy/dx de la función dada en las preguntas 12 a 15

Pregunta 12. x ^y + y ^x = 1

Solución:

Dado: x ^y + y ^x = 1

Consideremos

u = x ^y y v = y ^x

Asi que,

$\frac{du}{dx}+\frac{dv}{dx}=0$ ………(1)

Entonces primero tomamos u = x ^y

Al tomar el registro en ambos lados, obtenemos

logaritmo u = logaritmo(x ^y )

log u = y log x

Ahora, al derivar wrt x, obtenemos

$\frac{1}{u}.\frac{du}{dx}=y.\frac{d}{dx}\log x+\frac{dy}{dx}.\log x$

$\frac{1}{u}\frac{du}{dx}=\frac{y}{x}+\frac{dy}{dx}\log x$

$\frac{du}{dx}=x^4(\frac{y}{x}+\frac{dy}{dx}\log x)$ ………(2)

Ahora tomamos v = y ^x

Al tomar el registro en ambos lados, obtenemos

registro v = registro (y) ^x

log v = x log y

Ahora, al derivar wrt x, obtenemos

$\frac{1}{v}.\frac{dv}{dx}=x\frac{d}{dx}(\log x)+\log y\frac{d}{dx}x$

$\frac{dv}{dx}=v(x.\frac{1}{y}.\frac{dy}{dx}+\log y)$

$\frac{dv}{dx}=y^x(\frac{x}{y}\frac{dy}{dx}+\log x)$ ………(3)

Ahora ponga todos los valores de eq(2) y (3) en eq(1)

$x^y(\frac{y}{x}+\frac{dy}{dx}\log x)+y^x(\frac{x}{y}\frac{dy}{dx}+\log y)=0$

$(x^y.\log x+xy^{x-1})\frac{dy}{dx}=-(yx^{y-1}+y^x\log y)$

$\frac{dy}{dx}=\frac{-yx^{y-1}+y^x\log y}{x^y\log x+xy^{x-1}}$

Pregunta 13. y ^x = x ^y

Solución:

Dado: y ^x = x ^y

Al tomar el registro en ambos lados, obtenemos

log(yx) = log(x ^y )

xlog y = y log x

Ahora, al derivar wrt x, obtenemos

$x\frac{dy}{dx}(\log y)+\log y(\frac{d}{dx}x)=y\frac{d}{dx}\log x+\log x\frac{d}{dx}y$

$x.\frac{d}{dx}.y+\log y.1=y.\frac{1}{x}+\log x\frac{dy}{dx}$

$\frac{x}{y}\frac{dy}{dx}+\log y=\frac{y}{x}+\log x\frac{dy}{dx}$

$(\frac{x}{y}-\log x)\frac{dy}{dx}=(\frac{y}{x}-\log y)$

$\frac{dy}{dx}=\frac{\frac{y}{x}-\log y}{\frac{x}{y}-\log x}$

$\frac{dy}{dx}=\frac{y}{x}(\frac{y-x\log y}{x-y\log x})$

Pregunta 14. (cos x) ^y = (cos y) ^x

Solución:

Dado: (cos x) ^y = (cos y) ^x

Al tomar el registro en ambos lados, obtenemos

y log(cos x) = x log (cos y)

Ahora, al derivar wrt x, obtenemos

$y\frac{d}{dx}\log(\cos x)+\log(\cos x).\frac{dy}{dx}=x\frac{d}{dx}\log (\cos y)+\log(\cos y)\frac{dx}{dx}$

$y\frac{1}{\cos x}\frac{d}{dx}\cos x+\log(\cos x)\frac{dy}{dx}=x\frac{1}{\cos y}\frac{d}{dx}\cos y+\log(\cos y).1$

$\frac{y}{\cos x}.-\sin x+\log(\cos x).\frac{dy}{dx}=\frac{x}{\cos y}.(-\sin y).\frac{dy}{dx}+\log(\cos y)$

$(\log(\cos x)+x\tan y)\frac{dy}{dx}=\log(\cos y)+y \tan x$

$\frac{dy}{dx}=\frac{\log(\cos y)+y\tan x}{\log(\cos x)+x\tan y}$

Pregunta 15. xy = e ^{(x – y)}

Solución:

Dado: xy = e ^{(x – y)}

Al tomar el registro en ambos lados, obtenemos

log(xy) = log e ^{x – y}

registro x + registro y = x – y

Ahora, al derivar wrt x, obtenemos

$\frac{d}{dx}\log x+\frac{d}{dx}\log y=\frac{dx}{dx}-\frac{dy}{dx}$

$\frac{1}{x}.+\frac{1}{y}.\frac{dy}{dx}=1-\frac{dy}{dx}$

$(\frac{1}{y}+1)\frac{dy}{dx}=(1-\frac{1}{x})$

$\frac{dy}{dx}=\frac{(1-\frac{1}{x})}{(1+\frac{1}{y})}$

$\frac{dy}{dx}=\frac{y(x-1)}{x(y+1)}$

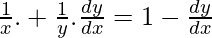
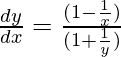
Pregunta 16. Encuentra la derivada de la función dada por f(x) = (x + 1)(x + x ² )(1 + x ⁴ )(1 + x ⁸ ) y por lo tanto encuentra f'(1).

Solución:

Dado: f(x) = (x + 1)(x + x ² )(1 + x ⁴ )(1 + x ⁸ )

Hallar: f'(1)

Al tomar el registro en ambos lados, obtenemos

log(f(x)) = log(1 + x) + log(1 + x ² ) + log(1 + x ⁴ ) + log(1 + x ⁸ )

Ahora, al derivar wrt x, obtenemos

$\frac{1}{f(x)}.\frac{d}{dx}f{x}=\frac{1}{1+x}\frac{d}{dx}(1+x)+\frac{1}{1+x^2}(1+x)^2+\frac{1}{1+x^4}.\frac{d}{dx}(1+x^4)+\frac{1}{1+x^8}\frac{d}{dx}(1+x^8)\frac{f'(x)}{f(x)}=\frac{1}{1+x}+\frac{2x}{1+x^2}+\frac{4x^3}{1+x^4}+\frac{8x^7}{1+x^8}$

$f'(x)=(1+x)(1+x^2)(1+x^4)(1+x^8)(\frac{1}{1+x}+\frac{2}{1+x^2}+\frac{4x^3}{1+x^2}+\frac{8x^7}{1+x^8})$

∴ f'(1) = 2.2.2.2. $(\frac{1}{2}+\frac{2}{2}+\frac{4}{2}+\frac{8}{2})$

$f'(1)=16.(\frac{15}{2})$

f'(1) = 120

Pregunta 17. Diferencie (x ⁵ – 5x + 8)(x ³ + 7x + 9) de las tres formas mencionadas a continuación

(i) Usando la regla del producto

(ii) Expandiendo el producto para obtener un solo polinomio

(iii) Por diferenciación logarítmica.

¿Todos dan la misma respuesta?

Solución:

(i) Usando la regla del producto

$\frac{d}{dx}(u.v)=v\frac{du}{dv}+u\frac{dv}{dx}$

$\frac{dy}{dx}=(x^2-5x+8)\frac{d}{dx}(x^3+7x+9)+(x^3+7x+9).\frac{d}{dx}(x^2-5x+8)$

dy/dx = (3x ⁴ – 15x ³ + 24x ² + 7x ² – 35x + 56) + (2x ⁴ + 14x ² + 18x – 5x ³ – 35x – 45)

dy/dx = 5x ⁴ – 20x ³ + 45x ² – 52x + 11

(ii) Por expansión

y = (x2 ^– 5x + 8)(x3 ⁺ 7x + 9)

y = x ⁵ + 7x ³ + 9x ² – 5x ⁴ – 35x ² – 45x + 8x ³ + 56x + 72

y = x ⁵ – 5x ⁴ + 15x ³ – 26x ² + 11x + 72

dy/dx = 5x ⁴ – 20x ³ + 45x ² – 52x + 11

(iii) Por expansión logarítmica

Tomando registro en ambos lados

registro y = registro (x ² – 5x + 8) + registro (x ³ + 7x + 9)

Ahora al diferenciar wrt x, obtenemos

$\frac{1}{y}.\frac{dy}{dx}=\frac{1}{x^2-5x+8}.\frac{d}{dx}(x^2-5x+8)+\frac{1}{x^3+7x+9}\frac{d}{dx}(x^3+7x+9)$

$\frac{1}{y}.\frac{dy}{dx}=\frac{2x-5}{x^2-5x+8}+\frac{3x^2+7}{x^3+7x+9}$

$\frac{1}{(x^2-5x+8)(x^3+7x+9)}\frac{dy}{dx}=\frac{(2x-5)(x^3+7x+9)+(3x^2+7)(x^2-5x+8)}{(x^2-5x+8)(x^3+7x+9)}$

dy/dx = 2x ⁴ + 14x ² + 18x – 5x ³ – 35x – 45 + 3x ⁴ – 15x ³ + 24x ² + 7x ² – 35x + 56

dy/dx = 5x ⁴ – 20x ³ + 45x ² – 52x + 11

La respuesta es siempre la misma, sea cual sea el método que usemos.

Pregunta 18. Si u, v y w son función de x, entonces demuestre que

$\frac{d}{dx}(u.v.w)=\frac{du}{dx}v.w+u.\frac{dv}{dx}.w+u.v.\frac{dw}{dx}$

Solución:

Sea y = uvw

Método 1: Usar la regla del producto

$\frac{dy}{dx}=u\frac{d}{dx}(v.w)+v.w\frac{d}{dx}u$

$\frac{dy}{dx}=u.[v.\frac{dw}{dx}+w\frac{du}{dx}]+v.w.\frac{du}{dx}$

$\frac{dy}{dx}=u.v.\frac{dw}{dx}+u.w.\frac{dv}{dx}+v.w\frac{du}{dx}$

Método 2: Usando diferenciación logarítmica

Tomando registro en ambos lados

log y = log u + log v + log w

Ahora, diferenciando wrt x

$\frac{1}{y}\frac{dy}{dx}=\frac{1}{u}\frac{du}{dx}+\frac{1}{v}\frac{dv}{dx}+\frac{1}{w}.\frac{dw}{dx}$

$\frac{dy}{dx}=(u.v.w)(\frac{1}{u}\frac{du}{dx}+\frac{1}{v}\frac{dv}{dx}+\frac{1}{w}\frac{dw}{dx})$

$\frac{dy}{dx}=v.w\frac{du}{dx}+uw\frac{dv}{dx}+uv\frac{dw}{dx}$

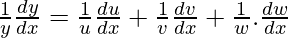
Publicación traducida automáticamente

Artículo escrito por ysachin2314 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 12 Soluciones NCERT – Matemáticas Parte I – Capítulo 5 Continuidad y diferenciabilidad – Ejercicio 5.5 | conjunto 2

Capítulo 5 Continuidad y Diferenciabilidad – Ejercicio 5.5 | Serie 1

Pregunta 11. Deriva la función con respecto a x.

(x cos x) ^x + (x sen x) ^1/x

Encuentre dy/dx de la función dada en las preguntas 12 a 15

Pregunta 12. x ^y + y ^x = 1

Pregunta 13. y ^x = x ^y

Pregunta 14. (cos x) ^y = (cos y) ^x

Pregunta 15. xy = e ^{(x – y)}

Pregunta 16. Encuentra la derivada de la función dada por f(x) = (x + 1)(x + x ² )(1 + x ⁴ )(1 + x ⁸ ) y por lo tanto encuentra f'(1).

Pregunta 17. Diferencie (x ⁵ – 5x + 8)(x ³ + 7x + 9) de las tres formas mencionadas a continuación

(i) Usando la regla del producto

(ii) Expandiendo el producto para obtener un solo polinomio

(iii) Por diferenciación logarítmica.

¿Todos dan la misma respuesta?

Pregunta 18. Si u, v y w son función de x, entonces demuestre que

$\frac{d}{dx}(u.v.w)=\frac{du}{dx}v.w+u.\frac{dv}{dx}.w+u.v.\frac{dw}{dx}$

Deja una respuesta Cancelar la respuesta

Capítulo 5 Continuidad y Diferenciabilidad – Ejercicio 5.5 | Serie 1

Pregunta 11. Deriva la función con respecto a x.

(x cos x) x + (x sen x) 1/x

Encuentre dy/dx de la función dada en las preguntas 12 a 15

Pregunta 12. x y + y x = 1

Pregunta 13. y x = x y

Pregunta 14. (cos x) y = (cos y) x

Pregunta 15. xy = e (x – y)

Pregunta 16. Encuentra la derivada de la función dada por f(x) = (x + 1)(x + x 2 )(1 + x 4 )(1 + x 8 ) y por lo tanto encuentra f'(1).

Pregunta 17. Diferencie (x 5 – 5x + 8)(x 3 + 7x + 9) de las tres formas mencionadas a continuación

(i) Usando la regla del producto

(ii) Expandiendo el producto para obtener un solo polinomio

(iii) Por diferenciación logarítmica.

¿Todos dan la misma respuesta?

Pregunta 18. Si u, v y w son función de x, entonces demuestre que

Deja una respuesta Cancelar la respuesta

(x cos x) ^x + (x sen x) ^1/x

Pregunta 12. x ^y + y ^x = 1

Pregunta 13. y ^x = x ^y

Pregunta 14. (cos x) ^y = (cos y) ^x

Pregunta 15. xy = e ^{(x – y)}

Pregunta 16. Encuentra la derivada de la función dada por f(x) = (x + 1)(x + x ² )(1 + x ⁴ )(1 + x ⁸ ) y por lo tanto encuentra f'(1).

Pregunta 17. Diferencie (x ⁵ – 5x + 8)(x ³ + 7x + 9) de las tres formas mencionadas a continuación