Pregunta 21. Dibuja un bosquejo aproximado de la curva 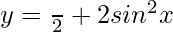 y encuentra el área entre el eje x, la curva y las ordenadas x = 0, x =
y encuentra el área entre el eje x, la curva y las ordenadas x = 0, x =
Solución:
Aquí, tenemos que encontrar el acotado por
eje x, x = 0 y x = π
Esta es la tabla de valores de
X 0 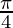
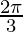
π 1.57 2.07 2,57 3,07 3.57 3,07 2,57 2.07 1.57 Aquí está el boceto aproximado,
La región sombreada representa el área requerida.
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y
Área del rectángulo = y△x
Los rectángulos aproximados se deslizan de x = 0 a x = π,
De este modo,
Área requerida = Región ABCDO
área requerida =
unidades cuadradas
Pregunta 22. Dibuja un bosquejo aproximado de la curva 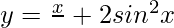 y encuentra el área entre el eje x, la curva y las ordenadas x = 0, x =
y encuentra el área entre el eje x, la curva y las ordenadas x = 0, x =
Solución:
Aquí, tenemos el área entre el eje y,
x = 0,
x = π
y
Por lo tanto, la tabla para la ecuación (1) es
X 0 π y 0 0.66 1.25 1.88 2,5 1,88 1,25 0,66 0
La región sombreada representa el área requerida.
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y
Área del rectángulo = y△x
Los rectángulos aproximados se deslizan de x = 0 a x = π,
De este modo,
Área requerida = Región ABOA
área requerida =
unidades cuadradas
Pregunta 23. Encuentra el área delimitada por la curva y = cos x entre x = 0 y x = 2
Solución:
Aquí de la figura podemos ver que
El área requerida = área de la región OABO + área de la región BCDB + área de la región DEFD
Por lo tanto,
El área requerida =
Pregunta 24. Muestre que las áreas bajo las curvas y = sen x y y = sen 2x entre x = 0 y x = 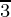 son la razón 2:3.
son la razón 2:3.
Solución:
Tenemos que encontrar el área bajo la curva.
y = sen x ……..(1)
y
y = sen 2x …………(2)
Entre x = 0 y x =
X
y = sen x
y = sen 2x 0 0,8 1 0,8 0 Aquí está el boceto aproximado
Área bajo la curva y = sen 2x
La región sombreada representa el área requerida.
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y1
Área del rectángulo = y1△x
Los rectángulos aproximados se deslizan de x = 0 a x =
,
De este modo,
Área requerida = Región OPACO
Lo cortamos en un rectángulo de aproximación de
Ancho = △x
Longitud = y2
Área del rectángulo = y2△x
Los rectángulos aproximados se deslizan de x = 0 a x =
,
De este modo,
Área requerida = Región OQACO
De este modo,
Pregunta 25. Compara el área bajo las curvas y = cos 2 x e y = sen 2 x entre x = 0 y x =
Solución:
Aquí para comparar el área bajo las curvas
y = cos 2 x
y
y = sen 2 x
Entre x = 0 y x =
Esta es la tabla para y = cos 2 x y y = sen 2 x
X
y = cos 2 x
0
1
y = sen 2 x 0 0,25 0,5 0.75 1 0,75 0,5 0.25 0
Área de la región encerrada por
y = cos 2 x y eje
A 1 = Región OABO + Región BCDB
= 2 (Región BCDB)
![Rendered by QuickLaTeX.com \displaystyle =2\int_{\frac{\pi}{2}}^\pi cos^2x\ dx\\ =2\int_{\frac{\pi}{2}}^\pi\left(\frac{1-cos\ 2x}{2}\right)\ dx\\ =\left[x-\frac{sin\ 2x}{2}\right]^\pi_{\frac{\pi}{2}}\\ =\left[(x-0)-\left(\frac{\pi}{2}-0\right)\right]\\ =\pi-\frac{\pi}{2}\\ A_1=\frac{\pi}{2}\ sq.\ units\ \ \ \ \ \ .....(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bf07ace77f6d331628dfd69e95190cdd_l3.png)
Área de región encerrada por y = sen 2 x y eje
A 2 = Región OEDO
De la ecuación (1) y (2),
UN 1 = UN 2
De este modo,
Área encerrada por y = cos 2 x = Área encerrada por y = sen 2 x.
Pregunta 26. Encuentra el área delimitada por la elipse 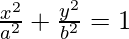 y las ordenadas x = 0 y x = ae, donde, b 2 = a 2 (1 – e 2 ) y e < 1.
y las ordenadas x = 0 y x = ae, donde, b 2 = a 2 (1 – e 2 ) y e < 1.
Solución:
Por lo tanto, el área requerida en la figura siguiente de la región BOB’RFSB está encerrada por la elipse y las líneas x = 0 y x = ae
Aquí está el área de la región BOB’RFSB
Pregunta 27. Encuentra el área del segmento menor del círculo x 2 + y 2 = a 2 cortado por la línea x = 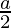 .
.
Solución:
Área del segmento de espejo del círculo.
Pregunta 28. Encuentra el área de la región delimitada por la curva x = at, y = 2at entre las ordenadas correspondientes t = 1 y t = 2.
Solución:
Área de la región delimitada
Pregunta 29. Encuentra el área encerrada por la curva x = 3 cos t, y = 2 sin t.
Solución:
Área de la región delimitada
= -8 [0 – 1]
= 8 unidades cuadradas
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

![Rendered by QuickLaTeX.com \displaystyle =\int_0^π y\ dx\\ =\int_0^π\left(\frac{π}{2}+2sin^2x\right)\ dx\\ =\int_0^π\left(\frac{π}{2}+1-cos\ 2x\right)\ dx\\ =\left[\frac{π}{2}x+x-\frac{sin\ 2x}{2}\right]_0^π\\ =\left[\left(\frac{π^2}{2}+π-\frac{sin\ 2x}{2}\right)-(0)\right]\\ =\frac{π^2}{2}+π](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7f865d4abaf4120e4995656737314fcb_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =\int_0^π y\ dx\\ =\int_0^π\left(\frac{π}{2}+2sin^2x\right)\ dx\\ =\int_0^π\left(\frac{π}{2}+1-cos\ 2x\right)\ dx\\ =\left[\frac{π}{2x}x+x-\frac{sin\ 2x}{2}\right]_0^π\\ =\left[\left(\frac{π^2}{2x}+π-0\right)-(0)\right]\\](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-496f3758bb65ab8e61f045dee8ec1fbf_l3.png)

![Rendered by QuickLaTeX.com \displaystyle \int_0^{\frac{\pi}{2}}cos\ x\ dx+\left|\int_{\frac{\pi}{2}}^{\frac{3\pi}{2}}cos\ x\ dx\right|+\int_{\frac{3\pi}{2}}^{2\pi}cos\ x\ dx\\ =[sin\ x]_0^{\frac{\pi}{2}}+\left|[sin\ x]^{\frac{3\pi}{2}}_{\frac{\pi}{2}}\right|+[sin\ x]^{2\pi}_{\frac{3\pi}{2}}\\ =\left[sin\frac{\pi}{2}-sin0\right]+\left|sin\frac{3\pi}{2}-sin\frac{\pi}{2}\right|+\left[sin\ 2x-sin\frac{3\pi}{2}\right]\\ =1+2+1\\ =4\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c3e8c10bbb0fa0b6f935bcb6851dbb87_l3.png)
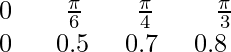

![Rendered by QuickLaTeX.com \displaystyle A_1=\int_0^{\frac{\pi}{3}}y_1\ dx\\ =\int_0^{\frac{\pi}{3}}sin\ 2x\ dx\\ =\left[\frac{-cos\ 2x}{2}\right]_0^{\frac{\pi}{3}}\\ =-\left[-\frac{1}{4}-\frac{1}{2}\right]\\ A_1=\frac{3}{4}\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-838c430cb6d40ea9a02fa90fdb740a49_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =\int_0^{\frac{\pi}{3}}y_2\ dx\\ =\int_0^{\frac{\pi}{3}}sin\ x\ dx\\ =\left[{-cos\ x}\right]_0^{\frac{\pi}{3}}\\ =-\left[\frac{1}{2}-1\right]\\ A_2=\frac{1}{2}\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4a1f7b73ad10126ac57d5c915c6a9081_l3.png)
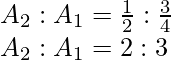
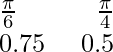
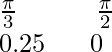
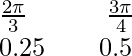

![Rendered by QuickLaTeX.com \displaystyle =\int_{0}^\pi sin^2x\ dx\\ =\int_{0}^\pi\left(\frac{1-cos\ 2x}{2}\right)\ dx\\ =\frac{1}{2}\left[x-\frac{sin\ 2x}{2}\right]^\pi_{0}\\ =\frac{1}{2}[(x-0)-(0)]\\ A_2=\frac{\pi}{2}\ sq.\ units\ \ \ \ \ \ .....(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0fb8f0311d8277da1e516732c28c06f3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle =2\int_0^{ae}y\ dx\\ =2\frac{b}{a}\int_0^{ae}\sqrt{a^2-x^2}\ dx\\ =\frac{2b}{a}\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{a}\right]_0^{ae}\\ =\frac{2b}{2a}\left[ae\sqrt{a^2-a^2e^2}+a^2sin^{-1}e\right]\\ =ab\left[e\sqrt{1-e^2}+sin^{-1}e\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b307f84a5083366669bbb4b66c82315_l3.png)


![Rendered by QuickLaTeX.com \displaystyle =2\int_{\frac{a}{2}}^a\sqrt{a^2-x^2}\ dx\\ =2\left[\frac{x}{2}\sqrt{a^2-x^2}+\frac{a^2}{2}sin^{-1}\frac{x}{2}\right]_{\frac{a}{2}^a}\\ =2\left[\frac{a}{2}(0)+\frac{a^2}{2}sin^{-1}\left(\frac{a}{2}\right)-\frac{a}{4}\sqrt{a^2-\frac{a^2}{4}}-\frac{a^2}{2}sin^{-1}\frac{a}{4}\right]\\ =2\left[\frac{a^2}{2}sin^{-1}\left(\frac{a}{2}\right)-\frac{a}{4}\sqrt{a^2-\frac{a^2}{4}}-\frac{a^2}{2}sin^{-1}\frac{a}{4}\right]\\ =\frac{a^2}{12}[4\pi-3\sqrt3]\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e1244b5ee52b8619fbf1ec442631103b_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =2\int_1^2y\ \frac{dx}{dt}\ dt\\ =2\int_1^2(2at)(2at)\ dt\\ =8a^2\int_1^2t^2\ dt\\ =8a^2\left[\frac{t^3}{3}\right]_1^2\\ =8a^2\left[\frac{8}{3}-\frac{1}{3}\right]\\ =\frac{56a^2}{3}\ sq.\ units](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2cfd12dc75df476e1d6913076e3adf21_l3.png)

![Rendered by QuickLaTeX.com \displaystyle =4\int_0^{\frac{\pi}{2}}2sin\ t\ dt\\ =-8[cos\ t]_0^{\frac{\pi}{2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7225c4397ecf1921ef7418a44c3f40b4_l3.png)