Capítulo 16 Comprender los cuadriláteros de formas – Ejercicio 16.1 | Serie 1
Pregunta 13. En la Figura, encuentra la medida de ∠MPN.
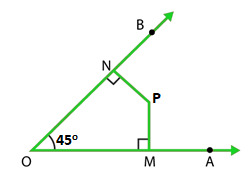
Solución:
Como sabemos que la suma de los ángulos de un cuadrilátero es = 360°
En el cuadrilátero MPNO
∠NOP = 45°, ∠OMP = ∠PNO = 90° (Dado)
Supongamos que el ángulo ∠MPN es x°
∠NOP + ∠OMP + ∠PNO + ∠MPN = 360°
45° + 90° + 90° + x° = 360°
x° = 360° – 225°
x° = 135°
Por lo tanto, la medida de ∠MPN es 135°
Pregunta 14. Los lados de un cuadrilátero se producen en orden. ¿Cuál es la suma de los cuatro ángulos exteriores?
Solución:
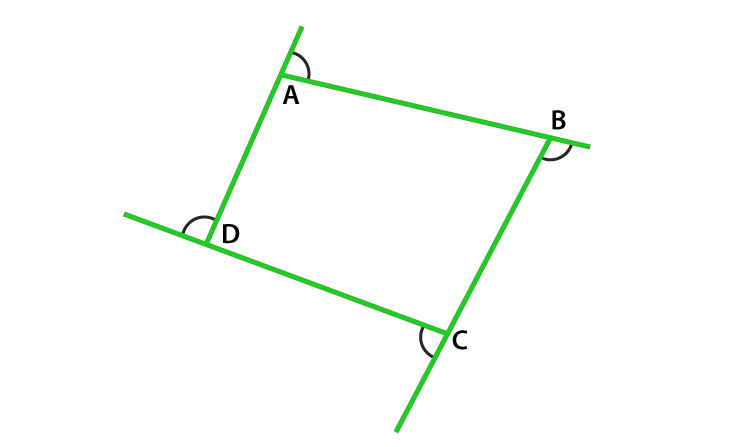
Como sabemos que, ángulo exterior + ángulo interior adyacente = 180° (Par lineal)
Aplicación de la relación para un polígono de n lados
Suma de todos los ángulos exteriores + Suma de todos los ángulos interiores = n × 180°
Suma de todos los ángulos exteriores = n × 180° – Suma de todos los ángulos interiores
= n × 180° – (n -2) × 180° (La suma de los ángulos interiores es = (n – 2) x 180°)
= norte × 180° – norte × 180° + 2 × 180°
= 180°n – 180°n + 360° = 360°
Por lo tanto, la suma de cuatro ángulos exteriores es 360 o
Pregunta 15. En la figura, las bisectrices de ∠A y ∠B se encuentran en un punto P. Si ∠C =100° y ∠D = 50°, encuentra la medida de ∠APB.
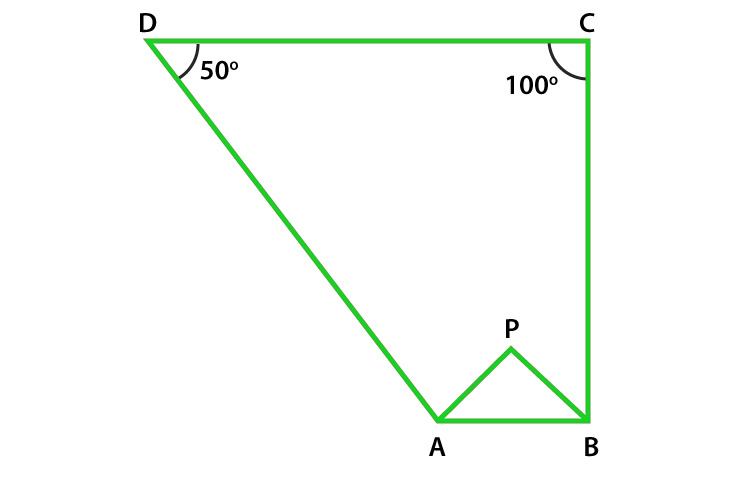
Solución:
Como sabemos que la suma de los ángulos de un cuadrilátero es = 360°
En el cuadrilátero ABCD
Dado que,
∠C =100° y ∠D = 50°
∠A + ∠B + ∠C+ ∠D = 360 o
∠A + ∠B + 100 o + 50 o = 360 o
∠A + ∠B = 360o – 150o
∠A + ∠B = 210 o (Ecuación 1)
Ahora en Δ APB
½ ∠A + ½ ∠B + ∠APB = 180 o (la suma del triángulo es 180 o )
∠APB = 180 o – ½ (∠A + ∠B) (Ecuación 2)
Al sustituir el valor de ∠A + ∠B = 210 de la ecuación (1) en la ecuación (2)
∠APB = 180 o – ½ (210 o )
= 180 o – 105 o = 75 o
Por lo tanto, la medida de ∠APB es 75 o .
Pregunta 16. En un cuadrilátero ABCD, los ángulos A, B, C y D están en la razón 1:2:4:5. Encuentra la medida de cada ángulo del cuadrilátero.
Solución:
Como sabemos que la suma de los ángulos de un cuadrilátero es = 360°
Sea cada ángulo x o
Por lo tanto,
xo + 2x o + 4x o + 5x o = 360 o
12x o = 360 o
x o = 360 o /12 = 30 o
El valor de los ángulos es x = 30 o ,
2x = 2 × 30 = 60o
4x = 4 × 30 = 120 o
5x = 5 × 30 = 150 o
Por lo tanto, el valor de los ángulos es 30 o , 60 o , 120 o , 150 o .
Pregunta 17. En un cuadrilátero ABCD, CO y DO son las bisectrices de ∠C y ∠D respectivamente. Demuestra que ∠COD = 1/2 (∠A +∠B).
Solución:
Como sabemos que la suma de los ángulos de un cuadrilátero es 360°
En el cuadrilátero ABCD
Por lo tanto,
∠A + ∠B + ∠C+ ∠D = 360 o
∠A + ∠B = 360o – (∠C+ ∠D)
½ (∠A + ∠B) = ½ [360 o – (∠C+ ∠D)]
= 180 o – ½ (∠C+ ∠D) (Ecuación 1)
Ahora en Δ DOC
½ ∠D + ½ ∠C+ ∠COD = 180 o (Sabemos que la suma del triángulo = 180o)
½ (∠C+ ∠D) + ∠COD = 180 o
∠COD = 180 o – ½ (∠C+ ∠D) (Ecuación 2)
En las ecuaciones (1) y (2) RHS es igual, entonces LHS también será igual.
Por lo tanto, se prueba ∠COD = ½ (∠A + ∠B).
Pregunta 18. Halla el número de lados de un polígono regular, cuando cada uno de sus ángulos mide
(i) 160°
(ii) 135°
(iii) 175°
(iv) 162°
(v) 150°
Solución:
La suma de los ángulos interiores A de un polígono de n lados viene dada por A = [(n-2) ×180o] /n
(i) 160 o
El ángulo del cuadrilátero es 160° (Dado)
160 o = [(n-2) ×180 o ]/n
160 o n = (n-2) ×180 o
160 o n = 180 o n – 360 o
180 o n – 160 o n = 360 o
20 o n = 360 o
n = 360 o /20 = 18
Por lo tanto el numero de lados es 18
(ii) 135 o
El ángulo del cuadrilátero es 135° (Dado)
135 o = [(n-2) ×180 o ]/n
135 o n = (n-2) ×180 o
135 o = 180 o – 360 o
180 o n – 135 o n = 360 o
45 o n = 360 o
n = 360 o / 45 = 8
Por lo tanto, el número de lados es 8
(iii) 175 o
El ángulo del cuadrilátero es 175° (Dado)
175 o = [(n-2) ×180 o ]/n
175 o n = (n-2) ×180 o
175 o n = 180 o n – 360 o
180 o n – 175 o n = 360 o
5 o n = 360 o
n = 360 o /5 = 72
Por lo tanto, el número de lados es 72
(iv) 162 o
El ángulo del cuadrilátero es 162° (Dado)
162 o = [(n-2) ×180 o ]/n
162 o n = (n-2) ×180 o
162 o n = 180 o – 360 o
180 o n – 162 o n = 360 o
18 o n = 360 o
n = 360 o /18 = 20
Por lo tanto, el número de lados es 20
(v) 150 o
El ángulo del cuadrilátero es 160° (Dado)
150 o = [(n-2) ×180 o ]/n
150 o n = (n-2) ×180 o
150 o n = 180 o n – 360 o
180 o n – 150 o n = 360 o
30 o n = 360 o
n = 360 o /30 = 12
Por lo tanto, el número de lados es 12
Pregunta 19. Encuentra el número de grados en cada ángulo exterior de un pentágono regular.
Solución:
Como sabemos que la suma de los ángulos exteriores de un polígono es 360°
Suma de cada ángulo exterior de un polígono = 360 o /n (n es el número de lados)
Como sabemos que el número de lados en un pentágono es 5
Suma de cada ángulo exterior de un pentágono = 360 o /5 = 72 o
Por lo tanto, la medida de cada ángulo exterior de un pentágono es 72 o
Pregunta 20. La medida de los ángulos de un hexágono son x°, (x-5)°, (x-5)°, (2x-5)°, (2x-5)°, (2x+20)°. Encuentra el valor de x.
Solución:
Como sabemos que la suma de los ángulos interiores de un polígono = (n – 2) × 180° (n = número de lados del polígono)
Como sabemos que el hexágono tiene 6 lados por lo tanto,
La suma de los ángulos interiores de un hexágono = (6 – 2) × 180° = 4 × 180° = 720°
x°+ (x-5)°+ (x-5)°+ (2x-5)°+ (2x-5)°+ (2x+20)° = 720°
x°+ x°- 5°+ x° – 5°+ 2x° – 5°+ 2x° – 5°+ 2x° + 20° = 720°
9x° = 720°
x = 720 o /9 = 80 o
Por lo tanto, el valor de x es 80 o
Pregunta 21. En un hexágono convexo, demuestre que la suma de todos los ángulos interiores es igual al doble de la suma de sus ángulos exteriores formados al producir los lados en el mismo orden.
Solución:
Como sabemos que la suma de los ángulos interiores de un polígono = (n – 2) × 180°
La suma de los ángulos interiores de un hexágono = (6 – 2) × 180° = 4 × 180° = 720°
La suma de los ángulos exteriores de un polígono es 360°
Por lo tanto Suma de los ángulos interiores de un hexágono = Dos veces la suma de los ángulos interiores.
Por lo tanto probado.
Pregunta 22. La suma de los ángulos interiores de un polígono es tres veces la suma de sus ángulos exteriores. Determina el número de lados del polígono.
Solución:
Como sabemos que la suma de los ángulos interiores de un polígono = (n – 2) × 180° (i)
La suma de los ángulos exteriores de un polígono es 360°
por lo tanto,
Suma de ángulos interiores = 3 × suma de ángulos exteriores
= 3 × 360° = 1080° (ii)
Ahora igualando (i) y (ii) obtenemos,
(n – 2) × 180° = 1080°
n – 2 = 1080 o /180 o
n-2 = 6
norte = 6 + 2 = 8
Por lo tanto, el número de lados de un polígono es 8.
Pregunta 23. Determinar el número de lados de un polígono cuyos ángulos exteriores e interiores están en la razón 1 : 5.
Solución:
Como sabemos que la suma de los ángulos interiores de un polígono = (n – 2) × 180° (i)
La suma de los ángulos exteriores de un polígono es 360°
Como sabemos que Suma de ángulos exteriores / Suma de ángulos interiores = 1/5 (ii)
Igualando (i) y (ii) obtenemos,
360º /(n – 2) × 180 ° = 1/5
(n – 2) × 180° = 360 ° × 5
(n – 2) × 180° = 1800 o
(n – 2) = 1800 o /180 o
(n-2) = 10
norte = 10 + 2 = 12
Por lo tanto, el número de lados de un polígono es 12.
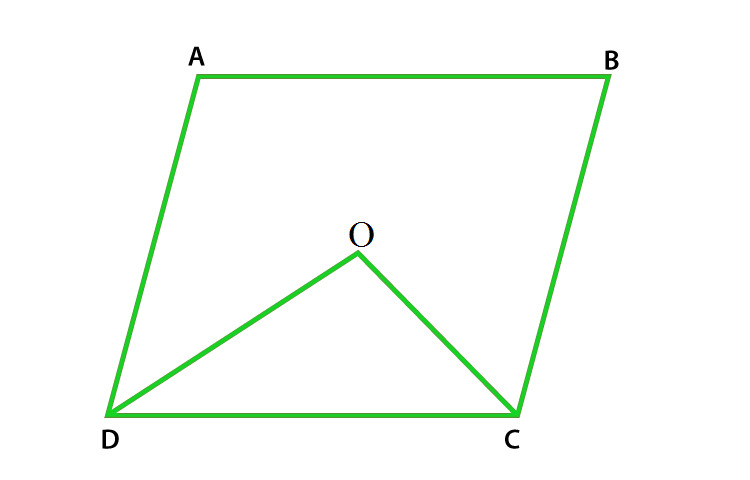
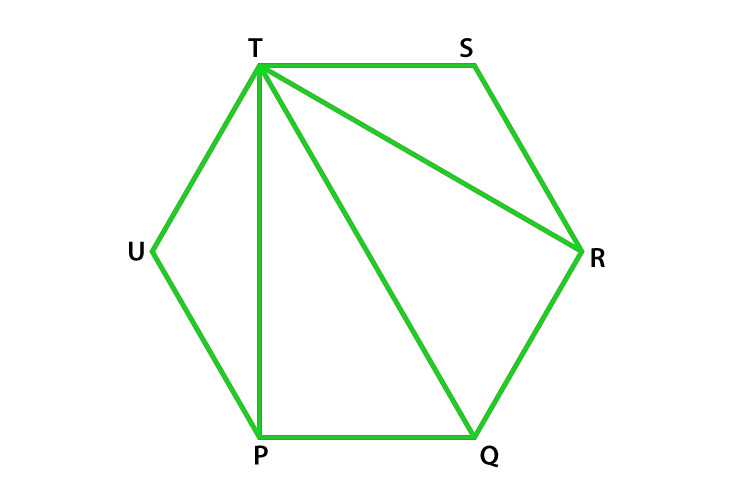
Pregunta 24. PQRSTU es un hexágono regular, determina cada ángulo de ΔPQT.
Solución:
Como sabemos que la suma de los ángulos interiores de un polígono = (n – 2) × 180°
La suma de los ángulos interiores de un hexágono = (6 – 2) × 180° = 4 × 180° = 720°
Suma de cada ángulo del hexágono = 720 o /6 = 120 o
∠PUT = 120 o Demostrado.
En Δ PONER
∠PUT + ∠UTP + ∠TPU = 180 o (suma de triángulos)
120o + 2∠UTP = 180 o (Ya que Δ PUT es un triángulo isósceles)
2∠UTP = 180 o – 120 o
2∠UTP = 60 o
∠UTP = 60 o /2 = 30 o
∠UTP = ∠TPU = 30 o de manera similar ∠RTS = 30 o
por lo tanto ∠PTR = ∠UTS – ∠UTP – ∠RTS
= 120 o – 30 o – 30 o = 60 o
∠TPQ = ∠UPQ – ∠UPT
= 120 o – 30 o = 90 o
∠TQP = 180 o – 150 o = 30 o (Usando la propiedad de suma de ángulos del triángulo en ΔPQT)
Por lo tanto ∠P = 90 o , ∠Q = 60 o , ∠T = 30 o
Publicación traducida automáticamente
Artículo escrito por ronilpatil y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA