Clase 8 Soluciones RD Sharma – Capítulo 8 División de expresiones algebraicas – Ejercicio 8.5

Pregunta 1: Divide el primer polinomio por el segundo polinomio en cada uno de los siguientes. Además, escribe el cociente y el resto:

(i) 3x ² + 4x + 5, x – 2

Solución:

3x ² + 4x + 5, x – 2

Usando el método de factorización,

$⇒\:\frac{\left(3x^2+4x+5\right)}{x-2} = \:\frac{3x\left(x-2)+10(x-2\right)+25}{x-2}$

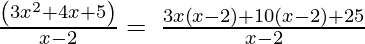
$=\:\frac{\left(x-2)(3x+10\right)+25}{x-2}$ (Tomando factor común (x-2))

$=(3x+10)+\:\frac{25}{x-2}$

∴ el Cociente es 3x + 10 y el Resto es 25.

(ii) 10x ² – 7x + 8, 5x – 3

Solución:

10x ² – 7x + 8, 5x – 3

Usando el método de factorización,

$⇒\:\frac{\left(10x^2-7x+8\right)}{5x-3} = \:\frac{\left(2x(5x-3)-\:\frac{1}{5}(5x-3)+\:\frac{37}{5}\right)}{5x-3}$

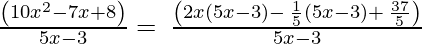
$=\:\frac{\left((5x-3)(2x-\:\frac{1}{5})+\:\frac{37}{5}\right)}{5x-3}$ (Tomando factor común (5x-3))

$=(2x-\:\frac{1}{5})+(\:\frac{\:\frac{37}{5}}{5x-3})$

∴ el Cociente es (2x – 1/5) y el Resto es 37/5.

(iii) 5y ³ – 6y ² + 6y – 1, 5y – 1

Solución:

5y ³ – 6y ² + 6y – 1, 5y – 1

Usando el método de factorización,

$⇒\:\frac{\left(5y^3-6y^2+6y-1\right)}{5y-1}= \:\frac{y^2\left(5y-1)-y(5y-1)+1(5y-1\right)}{5y-1}$

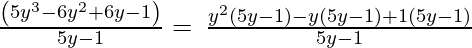
$=\:\frac{(5y-1)(y^2-y+1)}{5y-1}$ (Tomando factor común (5y-1))

$=(y^2-y+1)$

∴ el Cociente es (y ² – y + 1) y el Resto es 0.

(iv) x ⁴ – x ³ + 5x, x – 1

Solución:

x ⁴ – x ³ + 5x, x – 1

Usando el método de factorización,

$⇒\:\frac{\left(x^4-x^3+5x\right)}{x-1} = \:\frac{x^3\left(x-1)+5(x-1\right)+5}{x-1}$

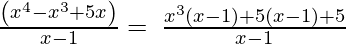
$=\:\frac{\left(x-1\right)(x^3+5)+5}{x-1}$ (Tomando factor común (x-1))

$=(x^3+5)+\:\frac{5}{x-1}$

∴ el Cociente es x ³ + 5 y el Resto es 5.

(v) y ⁴ + y ² , y ² – 2

Solución:

y ⁴ + y ² , y ² – 2

Usando el método de factorización,

$⇒\:\frac{\left(y^4+y^2\right)}{y^2-2}=\:\frac{y^2(y^2-2)+3(y^2-2)+6}{y^2-2}$

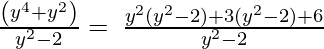
$=\:\frac{(y^2-2)(y^2+3)+6}{y^2-2}$ (Tomando factor común (y ² -2))

$=(y^2+3)+\:\frac{6}{y^2-2}$

∴ el Cociente es y ² + 3 y el Resto es 6.

Pregunta 2: Encuentra si el primer polinomio es o no un factor del segundo:

(yo) x + 1, 2x ² + 5x + 4

Solución:

x + 1, 2x ² + 5x + 4

Realicemos el método de factorización,

$⇒\:\frac{\left(2x^2+5x+4\right)}{x+1}= \:\frac{2x\left(x+1)+3(x+1\right)+1}{x+1}$

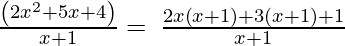
$=\:\frac{(x+1)(2x+3)+1}{x+1}$ (Tomando factor común (x+1))

$=(2x+3)+\:\frac{1}{x+1}$

Como el resto es 1, el primer polinomio no es un factor del segundo polinomio.

(ii) y – 2, 3y ³ + 5y ² + 5y + 2

Solución:

y – 2, 3y ³ + 5y ² + 5y + 2

Realicemos el método de factorización,

$⇒\:\frac{(3y^3+5y^2+5y+2)}{y-2}=\:\frac{3y^2(y-2)+11y(y-2)+27(y-2)+56}{y-2}$

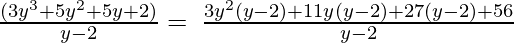
$=\:\frac{\left((y-2)(3y^2+11y+27)+56\right)}{y-2}$ (Tomando factor común (y-2))

$=(3y^2+11y+27)+\:\frac{56}{y-2}$

Como el resto es 56, el primer polinomio no es un factor del segundo polinomio.

(iii) 4x ² – 5, 4x ⁴ + 7x ² + 15

Solución:

4x ² – 5, 4x ⁴ + 7x ² + 15

Realicemos el método de factorización,

$⇒\:\frac{\left(4x^4+7x^2+15\right)}{4x^2-5}=\:\frac{x^2(4x^2-5)+3(4x^2-5)+30}{4x^2-5}$

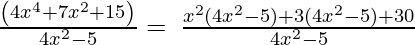
$=\:\frac{(4x^2-5)(x^2+3)+30}{4x^2-5}$ (Tomando factor común (4x ² -5))

$=(x^2+3)+\:\frac{30}{4x^2-5}$

Como el resto es 30, el primer polinomio no es un factor del segundo polinomio.

(iv) 4 – z, 3z ² – 13z + 4

Solución:

4 – z, 3z ² – 13z + 4

Realicemos el método de factorización,

$⇒\:\frac{\left(3z^2-13z+4\right)}{4-z} = \:\frac{\left(3z^2-12z-z+4\right)}{4-z}$

$=\:\frac{3z\left(z-4)-1(z-4\right)}{4-z}$ (Tomando factor común (z-4))

$=\:\frac{\left(z-4)(3z-1\right)}{4-z}$

$=\:\frac{\left(4-z)(1-3z\right)}{4-z}$

$=1-3z$

Como el resto es 0, el primer polinomio es un factor del segundo polinomio.

(v) 2a – 3, 10a ² – 9a – 5

Solución:

2a – 3, 10a ² – 9a – 5

Realicemos el método de factorización,

$⇒\:\frac{\left(10a^2-9a-5\right)}{2a-3}=\:\frac{5a\left(2a-3)+3(2a-3\right)+4}{2a-3}$

$=\:\frac{\left(2a-3)(5a+3\right)+4}{2a-3}$ (Tomando común (2a-3) común)

$=(5a+3)+\:\frac{4}{2a-3}$

Como el resto es 4, el primer polinomio no es factor del segundo polinomio.

(vi) 4y + 1, 8y ² – 2y + 1

Solución:

4 años + 1, 8 años ² – 2 años + 1

Realicemos el método de factorización,

$⇒\:\frac{\left(8y^2-2y+1\right)}{4y+1}=\:\frac{2y\left(4y+1)-1(4y+1\right)+2}{4y+1}$

$=\:\frac{\left(4y+1)(2y-1\right)+2}{4y+1}$ (Tomando factor común (4y+1))

$=(2y-1)+\:\frac{2}{4y+1}$

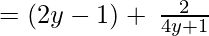
Como el resto es 2, el primer polinomio no es factor del segundo polinomio.

Publicación traducida automáticamente

Artículo escrito por apoorv__maheshwari y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1: Divide el primer polinomio por el segundo polinomio en cada uno de los siguientes. Además, escribe el cociente y el resto:

(i) 3x 2 + 4x + 5, x – 2

(ii) 10x 2 – 7x + 8, 5x – 3

(iii) 5y 3 – 6y 2 + 6y – 1, 5y – 1

(iv) x 4 – x 3 + 5x, x – 1

(v) y 4 + y 2 , y 2 – 2

Pregunta 2: Encuentra si el primer polinomio es o no un factor del segundo:

(yo) x + 1, 2x 2 + 5x + 4

(ii) y – 2, 3y 3 + 5y 2 + 5y + 2

(iii) 4x 2 – 5, 4x 4 + 7x 2 + 15

(iv) 4 – z, 3z 2 – 13z + 4

(v) 2a – 3, 10a 2 – 9a – 5

(vi) 4y + 1, 8y 2 – 2y + 1

Deja una respuesta Cancelar la respuesta

(i) 3x ² + 4x + 5, x – 2

(ii) 10x ² – 7x + 8, 5x – 3

(iii) 5y ³ – 6y ² + 6y – 1, 5y – 1

(iv) x ⁴ – x ³ + 5x, x – 1

(v) y ⁴ + y ² , y ² – 2

(yo) x + 1, 2x ² + 5x + 4

(ii) y – 2, 3y ³ + 5y ² + 5y + 2

(iii) 4x ² – 5, 4x ⁴ + 7x ² + 15

(iv) 4 – z, 3z ² – 13z + 4

(v) 2a – 3, 10a ² – 9a – 5

(vi) 4y + 1, 8y ² – 2y + 1