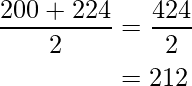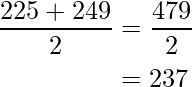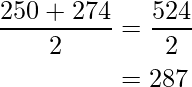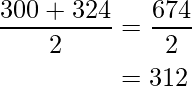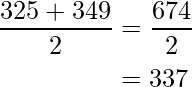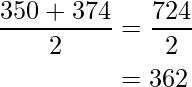Clase 9 RD Sharma- Capítulo 22 Representación tabular de datos estadísticos – Ejercicio 22.1 | conjunto 2

Pregunta 11. El número de carreras anotadas por un jugador de críquet en 25 entradas es el siguiente:

26, 35, 94, 48, 82, 105, 53, 0, 39, 42, 71, 0, 64, 15, 34, 15, 34, 6, 71, 0, 64, 15, 34, 15, 34, 67, 0, 42, 124, 84, 54, 48, 139, 64, 47

(i) Reorganice estas carreras en orden ascendente.

(ii) Determinar el jugador, es el puntaje más alto.

(iii) ¿Cuántas veces el jugador no anotó una carrera?

(iv) ¿Cuántos siglos anotó?

(v) ¿Cuántas veces anotó más de 50 carreras?

Solución:

(i) Organizar las carreras en orden ascendente como:

0, 0, 0, 0, 6, 15, 15, 15, 15, 26, 34, 34, 34, 34, 35, 39, 42, 42, 47, 48, 48, 53, 54, 64, 64, 64, 67, 71, 71, 82, 84, 90, 94, 124, 139.

(ii) De la disposición anterior, se observa que,

La puntuación más alta de todas las carreras es 139.

(iii) 3 veces, el jugador no logró anotar ninguna carrera.

(iv) Anotó 3 siglos en total.

(v) 12 veces, anotó más de 50 carreras.

Pregunta 12. El tamaño de la clase de distribución es 25 y el primer intervalo de clase es 200-224. Hay siete intervalos de clase.

(i) Escriba los intervalos de clase.

(ii) Escriba las marcas de clase de cada intervalo.

Solución:

Dado que,

El tamaño de la clase es igual a 25,

El primer intervalo de clase es 200-224

Hay siete intervalos de clase en total. 

(i) Estos intervalos de siete clases son los siguientes:

200-224, 225-249, 250-274, 275-299, 300-324, 325-349, 350-374.

(ii) Las marcas de clase de los siguientes intervalos de clase son:

• Para intervalo de clase, 200-224:

 

• Para intervalo de clase, 225-249:

• Para intervalo de clase, 250-274:

• Para intervalo de clase, 300-324:

• Para intervalo de clase, 325-349:

• Para intervalo de clase, 350-374:

Pregunta 13. Escriba el tamaño de la clase y los límites de la clase en cada uno de los siguientes:

(i) 104, 114, 124, 134, 144, 154 y 164

(ii) 47, 52, 57, 62, 67, 72, 78, 82, 87, 92, 97, 102

(iii) 12,5, 17,5, 22,5, 27,5, 32,5, 37,5, 42,5, 47,5

Solución:

(i) 104, 114, 124, 134, 144, 154 y 164

El tamaño de la clase para los datos dados es:

114 – 104 = 10

Los límites de clase se obtienen como: 

marca de clase	Límite de clase inferior	límite de clase superior	límite de clase
104	104 – 10/2 = 99	104 + 10/2 = 109	99 – 109
114	114 – 10/2 = 109	114 + 10/2 = 119	109 – 119
124	119	129	119 – 129
134	129	139	129 – 139
114	139	149	139 – 149
154	149	159	149 – 159
164	159	169	159 – 169

(ii) 47, 52, 57, 62, 67, 72, 78, 82, 87, 92, 97, 102

El tamaño de la clase para los datos dados es:

52 – 47 = 5

Los límites de clase se obtienen como:  

marca de clase	Límite de clase inferior	límite de clase superior	límite de clase
47	47 – 5/2 = 44,5	47 + 5/2 = 49,5	44,5 + 49,5
52	49.5	54.5	49,5 + 54,5
57	54.5	59.5	54,5 – 59,5
62	59.5	64.5	59,5 – 64,5
67	64.5	69.5	64,5 – 69,5
72	69.5	74.5	69,5 – 74,5
77	74.5	79.5	74,5 – 79,5
82	79.5	84.5	79,5 – 84,5
87	84.5	89.5	84,5 – 89,5
92	89.5	94.5	89,5 – 94,5
97	94.5	99.5	94,5 – 99,5
102	99.5	104.5	99,5 – 104,5

(iii) 12,5, 17,5, 22,5, 27,5, 32,5, 37,5, 42,5, 47,5

El tamaño de la clase para los datos dados es:

17,5 – 12,5 = 5

Los límites de clase se obtienen como: 

marca de clase	Límite de clase inferior	Límite de clase superior	límite de clase
12.5	12,5 – 2,5 = 10	12,5 + 2,5 = 15	10 – 15
17.5	17,5 – 2,5 = 15	17,5 + 2,5 = 20	15 – 20
22.5	22,5 – 2,5 = 20	22,5 + 2,5 = 25	20 – 25
27.5	27,5 – 2,5 = 25	27,5 + 2,5 = 30	25 – 30
32.5	32,5 – 2,5 = 30	32,5 + 2,5 = 35	30 – 35
37.5	37,5 – 2,5 = 35	37,5 + 2,5 = 40	35 – 40
42.5	42,5 – 2,5 = 40	42,5 + 2,5 = 45	40 – 45
47.5	47,5 – 2,5 = 45	47,5 + 2,5 = 50	45 – 50

Pregunta 14. Los siguientes datos dan el número de niños en 40 familias:

1, 2, 6, 5, 1, 5, 1, 3, 2, 6, 2, 3, 4, 2, 0, 0, 4, 4, 3, 2, 2, 0, 0, 1, 2, 2, 4, 3, 2, 1, 0, 5, 1, 2, 4, 3, 4, 1, 6, 2, 2.

Representarlo en forma de una distribución de frecuencias.

Solución:

La distribución de frecuencia de la siguiente secuencia de datos: 

Numero de niños	Marcas de conteo	Número de familias
0		5
1		7
2		12
3		5
4		6
5	|||	3
6	|||	3

Pregunta 15. Las calificaciones obtenidas por 40 estudiantes de la clase IX en matemáticas se dan a continuación:

81, 55, 68, 79, 85, 43, 29, 68, 54, 73, 47, 35, 72, 64, 95, 44, 50, 77, 64, 35, 79, 52, 45, 54, 70, 83, 62, 64, 72, 92, 84, 76, 63, 43, 54, 38, 73, 68, 52, 54.

Solución:

La obtención de la distribución de frecuencias de las notas obtenidas por 40 alumnos de la clase IX es la siguiente: 

Marcas	Marcas de conteo	Frecuencia
20 – 30	|	1
30 – 40	|||	3
40 – 50		5
50 – 60		8
60 – 70		8
70 – 80		9
80 – 90	||||	4
90 – 100	||	2
totales = 40

Pregunta 16. Las alturas (en cm) de 30 estudiantes de la clase IX se dan a continuación:

155, 158, 154, 158, 160, 148, 149, 150, 153, 159, 161, 148, 157, 153, 157, 153, 157, 162, 159, 151, 154, 156, 152, 156, 160, 152, 147, 155, 163, 155, 157, 153.

Prepare una tabla de distribución de frecuencias con 160 – 164 como uno de los intervalos de clase.

Solución:

La tabla de distribución de frecuencias con 160 – 164 como uno de los intervalos de clase es la siguiente: 

Altura (en cm)	Marcas de conteo	Frecuencia
145 – 149	||||	4
150 – 154		9
155 – 159		12
160 – 164		6
totales = 30

Pregunta 17. Los salarios mensuales de 30 trabajadores en una fábrica se dan a continuación:

830, 835, 890, 810, 835, 836, 869, 845, 898, 890, 820, 860, 832, 833, 855, 845, 804, 808, 812, 840, 885, 835, 836, 878, 840, 868, 890, 806, 840, 890.

Solución:

La obtención de la distribución de frecuencias para el salario mensual de 30 trabajadores en una fábrica es la siguiente: 

Altura (en cm)	Marcas de conteo	Frecuencia
800 – 810	|||	3
810 – 820	||	2
820 – 830	|	1
830 – 840		8
840 – 850		5
850 – 860	|	1
860 – 870	|||	3
870 – 880	|	1
880 – 890	|	1
890 – 900		5
totales = 30

Pregunta 18. Las temperaturas máximas diarias (en grados Celsius) registradas en cierta ciudad durante el mes de noviembre son las siguientes:

25.8, 24.5, 25.6, 20.7, 21.8, 20.5, 20.6, 20.9, 22.3, 22.7, 23.1, 22.8, 22.9, 21.7, 21.3, 20.5, 20.9, 23.1, 22.4, 21.5, 22.7, 22.8, 22.0, 23.9, 24.7, 24.7, 24.7. 22.8, 23.8, 24.6, 23.9, 21.1.

Solución:

La obtención de la distribución de frecuencias para las temperaturas máximas diarias (en grados centígrados) registradas en una determinada ciudad durante el mes de noviembre son las siguientes: 

Temperatura máxima (en grados Celsius)	Marcas de conteo	Frecuencia
20,0 – 21,0		6
21,0 – 22,0		5
22,0 – 23,0		9
23,0 – 24,0		5
24,0 – 25,0	|||	3
25,0 – 26,0	||	2
totales = 30

Pregunta 19. Construya una tabla de frecuencia con intervalos de clase iguales a partir de los siguientes datos sobre los salarios mensuales (en rupias) de 28 trabajadores que trabajan en una fábrica, tomando uno de los intervalos de clase como 210 – 230 (230 no incluido)

220, 268, 258, 242, 210, 268, 272, 242, 311, 290, 300, 320, 319, 304, 302, 218, 306, 292, 254, 278, 210, 240, 280, 316, 306, 215, 256, 236.

Solución:

La siguiente tabla muestra la distribución de frecuencias de los salarios mensuales (en rupias) de 28 trabajadores que trabajan en una fábrica: 

Salarios mensuales (en rupias)	Marcas de conteo	Frecuencia
210 – 230	||||	4
230 – 250	||||	4
250 – 270		5
270 – 290	|||	3
290 – 310		7
310 – 330		5
totales = 28

Pregunta 20. Las temperaturas mínimas diarias en grados Celsius registradas en cierta región ártica son las siguientes:

-12,5, -10,8, -18,6, -8,4, -10,8, -4,2, -4,8, -6,7, -13,2, -11,8, -2,3, -1,2, -2,6, 0, 2,4, 0, 3,2, 2,7, 3,4 , 0, -2,4, 0, 3,2, 2,7, 3,4, 0, -2,4, -5,8, -8,9, -14,6, -12,3, -11,5, -7,8, -2,9.

Represéntelos como una tabla de distribución de frecuencias tomando -19.9 a -15 como el intervalo de primera clase.

Solución:

La distribución de frecuencias con el límite inferior incluido y el límite superior excluido se representa tomando el primer intervalo de clase como -19,9 a -15:

La temperatura	Marcas de conteo	Frecuencia
-19,9 a -15	||	2
-15 a -10,1		7
-10,1 a -5,2		5
-5,2 a -0,3	||||	4
-0,3 a -4,6		17
totales = 35

Pregunta 21. Los grupos sanguíneos de 30 estudiantes de la clase VIII se registran de la siguiente manera:

A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O, A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O

Representa estos datos en forma de una tabla de distribución de frecuencias. Descubra cuál es el grupo sanguíneo más común y cuál es el más raro entre estos estudiantes.

Solución:

Dado que,

9 estudiantes de los grupos sanguíneos dados tienen el grupo sanguíneo A, 6 como B, 3 como AB y 12 como O

La tabla de frecuencia que representa los datos junto con la frecuencia correspondiente es la siguiente:

Grupo sanguíneo	Numero de estudiantes
A	9
B	6
AB	3
O	12
Total	30

Ya que, 12 estudiantes tienen su grupo sanguíneo como O, que es el máximo, por lo tanto el grupo sanguíneo más común es O. Además, 3 estudiantes tienen su grupo sanguíneo como AB, lo que implica que el grupo sanguíneo más raro es AB.

Pregunta 22. Se lanzaron tres monedas 30 veces. Cada vez que se produjo el número de caras se anotó de la siguiente manera:

0, 1, 2, 2, 1, 2, 3, 1, 3, 0

1, 3, 1, 1, 2, 2, 0, 1, 2, 1

3, 0, 1, 1, 2, 3, 2, 2, 0

Prepare una tabla de distribución de frecuencias para los datos dados anteriormente.

Solución:

La tabla de distribución de frecuencias para los datos de las tres monedas que se lanzan 30 veces se puede calcular de la siguiente manera:

Número de cabezas	Frecuencia
0	6
1	10
2	9
3	5
Total=30

Pregunta 23. Se preguntó a treinta niños sobre la cantidad de horas que vieron programas de televisión en la semana anterior. Los resultados se encontraron de la siguiente manera:

 1, 6, 2, 3, 5, 12, 5, 8, 4, 8

10, 3, 4, 12, 2, 8, 15, 1, 17, 6

3, 2, 8, 5, 9, 6, 8, 7, 14, 2.

(i) Haga una tabla de distribución de frecuencias para estos datos, tomando el ancho de clase 5 y uno de los intervalos de clase como 5 – 10.

(ii) ¿Cuántos niños veían la televisión durante 15 horas o más a la semana?

Solución:

(i) Los siguientes intervalos de clase son 0 – 5, 5 – 10, 10 – 15 construidos.

La tabla de distribución de frecuencias agrupadas teniendo en cuenta estos intervalos de clase es la siguiente:

Horas	Numero de niños
0 – 5	10
5 – 10	13
10 – 15	5
15 – 20	2
Total=30

(ii) El número de niños que vieron televisión durante al menos 15 horas a la semana es 2, lo que implica que el número de niños en el intervalo de clase 15 – 20 es equivalente a 2.