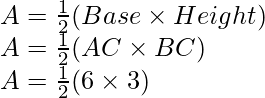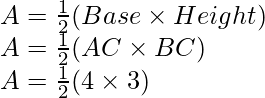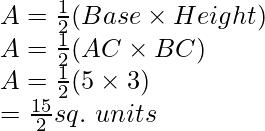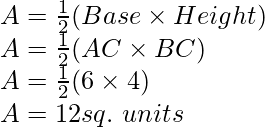Clase 9 Soluciones RD Sharma – Capítulo 13 Ecuación lineal en dos variables – Ejercicio 13.3

Pregunta 11: Dibuja la gráfica de la ecuación 2x + 3y = 12. A partir de la gráfica, encuentra las coordenadas del punto:

(i) cuyas coordenadas y son 3.

(ii) cuya coordenada x es −3.

Solución:

Dado:

2x + 3y = 12

Obtenemos,

$y=\frac{12-2x}{3}$

Sustituyendo x = 0 en y = $\frac{12-2x}{3}$ obtenemos,

$y=\frac{12-2\times0}{3}$

y = 4

Sustituyendo x = 6 en $y= \frac{12-2x}{3}$ , obtenemos

$y=\frac{12-2\times6}{3}$

y = 4

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 6

y 4 0

Trazando la ecuación dada en el gráfico, obtenemos el punto B (0, 4) y C (6,0).

(i) Las coordenadas del punto cuyo eje y es 3 son A $\left(\frac{3}{2},3\right)$

(ii) Las coordenadas del punto cuya coordenada x es –3 son D (-3, 6)

Pregunta 12: Dibuja la gráfica de cada una de las ecuaciones dadas a continuación. Además, encuentra las coordenadas de los puntos donde la gráfica corta los ejes de coordenadas:

(yo) 6x − 3y = 12

(ii) −x + 4y = 8

(iii) 2x + y = 6

(iv) 3x + 2y + 6 = 0

Solución:

(i) Dado:

6x – 3y = 12

Obtenemos,

$y=\frac{6x-12}{3}$

Ahora, reemplazando x = 0 en $y=\frac{6x-12}{3}$ , obtenemos

y = -4

Sustituyendo x = 2 en $y=\frac{6x-12}{3}$ , obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 2

y -4 0

Las coordenadas de los puntos donde el gráfico corta los ejes de coordenadas están en el eje y = -4 y x = 2

en el eje x.

(ii) Dado:

-x + 4y = 8

Obtenemos,

$y=\frac{8+x}{4}$

Ahora, reemplazando x = 0 en $y=\frac{8+x}{4}$ , obtenemos

y = 2

Sustituyendo x = -8 en $y=\frac{8+x}{4}$ , obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 -8

y 2 0

Las coordenadas de los puntos donde el gráfico corta los ejes de coordenadas están en el eje y = 2 y x = -8

en el eje x.

(iii) Dado:

2x + y = 6

Obtenemos,

y = 6 – 2x

Ahora, sustituyendo x= 0 en y = 6 – 2x obtenemos

y = 6

Sustituyendo x = 3 en y = 6 – 2x, obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 3

y 6 0

Las coordenadas de los puntos donde el gráfico corta los ejes de coordenadas son y = 6 en el eje y y x = 3

en el eje x.

(iv) Dado:

3x + 2y + 6 = 0

Obtenemos,

$y = \frac{-(6+3x)}{2}$

Ahora, reemplazando x = -2 en $y = \frac{-(6+3x)}{2}$ , obtenemos

y = -3

Sustituyendo x = -2 en $y = \frac{-(6+3x)}{2}$ , obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 -2

y -3 0

Las coordenadas de los puntos donde el gráfico corta los ejes de coordenadas son y = -3 en el eje y y x = -2

en el eje x.

Pregunta 13: Dibuja la gráfica de la ecuación 2x + y = 6. Sombrea la región delimitada por la gráfica y los ejes de coordenadas. Además, encuentre el área de la región sombreada.

Solución:

Dado:

2x + y = 6

Obtenemos,

y = 6 – 2 x

Ahora, reemplazando x = 0 en y = 6 – 2x, obtenemos

y = 6

Sustituyendo x = 3 en y = 6 – 2x, obtenemos

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 3

y 6 0

La región delimitada por el gráfico es ABC, que forma un triángulo.

AC en el eje y es la base del triángulo que tiene AC = 6 unidades en el eje y.

BC en el eje x es la altura del triángulo que tiene BC = 3 unidades en el eje x.

Por lo tanto,

Área del triángulo ABC, digamos que A está dada por

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(6\times3)$

A = 9 unidades cuadradas

Pregunta 14: Dibujar la gráfica de la ecuación 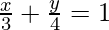$\frac{x}{3}+\frac{y}{4}=1$ . Además, encuentra el área del triángulo formado por la línea y los ejes de coordenadas.

Solución:

Dado:

$\frac{x}{3}+\frac{y}{4}=1$

4x + 3y = 12

Obtenemos,

$y=\frac{12-4x}{3}$

Ahora, reemplazando x = 0 en $y=\frac{12-4x}{3}$ , obtenemos

y = 4

Sustituyendo x = 3 en $y=\frac{12-4x}{3}$ , obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 3

y 4 0

La región delimitada por el gráfico es ABC, que forma un triángulo.

AC en el eje y es la base del triángulo que tiene AC = 4 unidades en el eje y.

BC en el eje x es la altura del triángulo que tiene BC = 3 unidades en el eje x.

Por lo tanto,

Área del triángulo ABC, digamos que A está dada por

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(4\times3)$

A = 6 unidades cuadradas

Pregunta 15: Dibuja la gráfica de y = | x |.

Solución:

Se nos da,

y = |x|

Sustituyendo, x = 1 obtenemos

y = 1

Sustituyendo, x = -1 obtenemos

y = 1

Sustituyendo x = 2 obtenemos

y = 2

Sustituyendo, x = -2 obtenemos

y = 2

Para cada valor de x, ya sea positivo o negativo, obtenemos y como un número positivo.

Pregunta 16: Dibuja la gráfica de y = | x | + 2.

Solución:

Dado:

y = |x| + 2

Sustituyendo, x = 0 obtenemos

y = 2

Sustituyendo, x = 1 obtenemos

y = 3

Sustituyendo, x = -1 obtenemos

y = 3

Sustituyendo, x = 2 obtenemos

y = 4

Sustituyendo, x = -2 obtenemos

y = 4

Para cada valor de x, ya sea positivo o negativo, obtenemos y como un número positivo y el valor mínimo de y es igual a 2 unidades.

Pregunta 17: Dibuja las gráficas de las siguientes ecuaciones lineales en el mismo papel cuadriculado:

2x + 3y = 12, x − y = 1

Encuentra las coordenadas de los vértices del triángulo formado por las dos líneas rectas y el área delimitada por estas líneas y el eje x.

Solución:

Dado:

2x + 3y = 12

Obtenemos,

$y=\frac{12-2x}{3}$

Ahora, reemplazando x = 0 en $y=\frac{12-2x}{3}$ , obtenemos

y = 4

Sustituyendo x = 6 en $y=\frac{12-2x}{3}$ , obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 6

y 4 0

Trazando A(0,4) y E(6,0) en la gráfica y uniendo los puntos , obtenemos la gráfica de la ecuación .

Dado:

x – y = 1

Obtenemos,

y = x − 1

Ahora, reemplazando x = 0 en y = x − 1, obtenemos

y = −1

Sustituyendo x = -1 en y = x − 1, obtenemos

y = −2

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 -1

y -1 -2

Trazando D(0,1) y E(-1,0) en la gráfica y uniendo los puntos , obtenemos la gráfica de la ecuación .

Por la intersección de las líneas formadas por 2x + 3y = 12 y x – y = 1 en el gráfico, se forma el triángulo ABC en el eje y.

Por lo tanto,

AC en el eje y es la base del triángulo ABC que tiene AC = 5 unidades en el eje y.

Dibuje FE perpendicular desde F en el eje y.

FE paralela al eje x es la altura del triángulo ABC que tiene FE = 3 unidades en el eje x.

Por lo tanto,

Área del triángulo ABC, digamos que A está dada por

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(5\times3)\\ =\frac{15}{2}sq.\ units$

Pregunta 18: Dibuja las gráficas de las ecuaciones lineales 4x − 3y + 4 = 0 y 4x + 3y −20 = 0. Encuentra el área delimitada por estas líneas y el eje x.

Solución:

Dado:

4x – 3y + 4 = 0

Obtenemos,

$y=\frac{4x+4}{3}$

Ahora, reemplazando x = 0 en $y=\frac{4x+4}{3}$ , obtenemos

$y=\frac{4}{3}$

Sustituyendo x = -1 en $y=\frac{4x+4}{3}$ , obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 -1

y $\frac{4}{3}$ 0

Trazando E(0, $\frac{4}{3}$ ) y A(-1,0) en la gráfica y uniendo los puntos, obtenemos la gráfica de la ecuación.

Se nos da,

4x + 3y – 20 = 0

Obtenemos,

$y=\frac{20-4x}{3}$

Ahora, reemplazando x = 0 en $y=\frac{20-4x}{3}$ , obtenemos

$y=\frac{20}{3}$

Sustituyendo x = 5 en $y=\frac{20-4x}{3}$ , obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 5

y $\frac{20}{3}$ 0

Trazando D(0, $\frac{20}{3}$ ) y B(5,0) en la gráfica y uniendo los puntos, obtenemos la gráfica de la ecuación.

Por la intersección de las líneas formadas por 4x – 3y + 4 = 0 y 4x + 3y – 20 = 0 en el gráfico, se forma el triángulo ABC en el eje x.

Por lo tanto,

AB en el eje x es la base del triángulo ABC que tiene AB = 6 unidades en el eje x.

Dibuje CF perpendicular desde C en el eje x.

CF paralelo al eje y es la altura del triángulo ABC que tiene CF = 4 unidades en el eje y.

Por lo tanto,

Área del triángulo ABC, digamos que A está dada por

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(6\times4)\\ A=12sq.\ units$

Pregunta 19: La trayectoria de un tren A viene dada por la ecuación 3x + 4y − 12 = 0 y la trayectoria de otro tren B viene dada por la ecuación 6x + 8y − 48 = 0. Representa gráficamente esta situación.

Solución:

Dado: Trayectoria del tren A,

3x + 4y – 12 = 0

Obtenemos,

$y=\frac{12-3x}{4}$

Ahora, reemplazando x = 0 en $y=\frac{12-3x}{4}$ , obtenemos

y = 3

Sustituyendo x = 4 en $y=\frac{12-3x}{4}$ , obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 4

y 3 0

Trazando A(4,0) y E(0,3) en la gráfica y uniendo los puntos , obtenemos la gráfica de la ecuación .

Nos dan la ruta del tren B,

6x + 8y – 48 = 0

Obtenemos,

$y=\frac{48-6x}{8}$

Ahora, reemplazando x = 0 en $y=\frac{48-6x}{8}$ , obtenemos

y = 6

Sustituyendo x = 8 en $y=\frac{48-6x}{8}$ , obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 8

y 6 0

Trazando C(0,6) y D(8,0) en la gráfica y uniendo los puntos , obtenemos la gráfica de la ecuación.

Pregunta 20: Ravish le dice a su hija Aarushi: “Hace siete años, yo tenía siete veces la edad que tenías tú entonces. Además, dentro de tres años tendré el triple de la edad que tú tendrás”. Si las edades actuales de Aarushi y Ravish son x e y años respectivamente, represente esta situación tanto algebraica como gráficamente.

Solución:

Se nos da la edad actual de Ravish como y años y Aarushi como x años.

Era de Ravish hace siete años = y – 7

Edad de Aarushi hace siete años = x – 7

Ravish ya ha dicho que hace siete años tenía siete veces la edad de Aarushi.

Asi que,

y-7 = 7(x-7)

y-7 = 7x-49

7x – y = -7 + 49

7x-y-42 = 0

Edad de Ravish dentro de tres años = y + 3

Edad de Aarushi dentro de tres años = x + 3

Ravish ya ha dicho que dentro de tres años él tendrá tres veces la edad de Aarushi.

Asi que,

y + 3 = 3(x + 3)

y + 3 = 3x + 9

3x + 9 – y – 3 = 0

3x – y + 6 = 0

(1) y (2) son la representación algebraica del enunciado dado.

Dado:

7x-y-42 = 0

Obtenemos,

y = 7x – 42

Ahora, sustituyendo x = 0 en y = 7x – 42, obtenemos

y = -42

Sustituyendo x = 6 en y = 7x – 42, obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 6

y -42 0

Dado:

3x – y + 6 = 0

Obtenemos,

y = 3x + 6

Ahora, reemplazando x = 0 en y = 3x + 6, obtenemos

y = 6

Sustituyendo x = -2 en y = 3x + 6, obtenemos

y = 0

Por lo tanto, tenemos la siguiente tabla que muestra las abscisas y ordenadas de los puntos en la línea representada por la ecuación dada

X 0 -2

y 6 0

La línea roja representa la ecuación. 7x-y-42 = 0

La línea azul representa la ecuación. 3x – y + 6 = 0

Pregunta 21: Aarushi conducía un automóvil con una velocidad uniforme de 60 km/h. Dibujar gráfica distancia-tiempo. A partir de la gráfica, encuentre la distancia recorrida por Aarushi en

(i) $2\frac{1}{2}$ Horas

(ii) $\frac{1}{2}$ Hora

Solución:

Aarushi conduce el automóvil con una velocidad uniforme de 60 km/h.

Representamos el tiempo en el eje X y la distancia en el eje Y

Ahora, gráficamente

Se sabe que el automóvil viaja con una velocidad uniforme de 60 km/h. Esto significa que el automóvil recorre una distancia de 60 km cada hora. Por lo tanto, el gráfico que obtenemos es de una línea recta.

Además, sabemos cuando el automóvil está en reposo, la distancia recorrida es 0 km, la velocidad es 0 km/h y el tiempo también es 0 h.

Por tanto, la recta dada pasará por O(0,0) y M(1,60).

Une los puntos O y M y extiende la línea en ambas direcciones.

Ahora, dibujamos una línea punteada paralela al eje y desde x = $\frac{1}{2}$ que se encuentra con el gráfico de línea recta en L desde la cual dibujamos una línea paralela al eje x que cruza el eje y en 30. Por lo tanto, en $\frac{1}{2}$ hr, la distancia recorrida por el coche tiene 30 km.

Ahora, dibujamos una línea punteada paralela al eje y desde x = $2\frac{1}{2}$ que se encuentra con el gráfico de línea recta en N desde la cual dibujamos una línea paralela al eje x que cruza el eje y en 150. Por lo tanto, en $2\frac{1}{2}$ hr, la distancia recorrida por el coche tiene 150 km.

(i) Distancia = Velocidad × Tiempo

La distancia recorrida en $2\frac{1}{2}$ horas está dada por

Distancia = $60\times2\frac{1}{2}$

Distancia = $60\times\frac{5}{2}$

Distancia = 150 kilómetros

(ii) Distancia = Velocidad × Tiempo

La distancia recorrida en $\frac{1}{2}$ horas está dada por

Distancia = $60\times\frac{1}{2}$

Distancia = 30 kilómetros

Publicación traducida automáticamente

Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 9 Soluciones RD Sharma – Capítulo 13 Ecuación lineal en dos variables – Ejercicio 13.3 | conjunto 2

Pregunta 11: Dibuja la gráfica de la ecuación 2x + 3y = 12. A partir de la gráfica, encuentra las coordenadas del punto:

Pregunta 12: Dibuja la gráfica de cada una de las ecuaciones dadas a continuación. Además, encuentra las coordenadas de los puntos donde la gráfica corta los ejes de coordenadas:

Pregunta 13: Dibuja la gráfica de la ecuación 2x + y = 6. Sombrea la región delimitada por la gráfica y los ejes de coordenadas. Además, encuentre el área de la región sombreada.

Pregunta 14: Dibujar la gráfica de la ecuación $\frac{x}{3}+\frac{y}{4}=1$ . Además, encuentra el área del triángulo formado por la línea y los ejes de coordenadas.

Pregunta 15: Dibuja la gráfica de y = | x |.

Pregunta 16: Dibuja la gráfica de y = | x | + 2.

Pregunta 17: Dibuja las gráficas de las siguientes ecuaciones lineales en el mismo papel cuadriculado:

Encuentra las coordenadas de los vértices del triángulo formado por las dos líneas rectas y el área delimitada por estas líneas y el eje x.

Pregunta 18: Dibuja las gráficas de las ecuaciones lineales 4x − 3y + 4 = 0 y 4x + 3y −20 = 0. Encuentra el área delimitada por estas líneas y el eje x.

Pregunta 19: La trayectoria de un tren A viene dada por la ecuación 3x + 4y − 12 = 0 y la trayectoria de otro tren B viene dada por la ecuación 6x + 8y − 48 = 0. Representa gráficamente esta situación.

Pregunta 21: Aarushi conducía un automóvil con una velocidad uniforme de 60 km/h. Dibujar gráfica distancia-tiempo. A partir de la gráfica, encuentre la distancia recorrida por Aarushi en

Deja una respuesta Cancelar la respuesta

Pregunta 11: Dibuja la gráfica de la ecuación 2x ​​+ 3y = 12. A partir de la gráfica, encuentra las coordenadas del punto:

Pregunta 12: Dibuja la gráfica de cada una de las ecuaciones dadas a continuación. Además, encuentra las coordenadas de los puntos donde la gráfica corta los ejes de coordenadas:

Pregunta 13: Dibuja la gráfica de la ecuación 2x ​​+ y = 6. Sombrea la región delimitada por la gráfica y los ejes de coordenadas. Además, encuentre el área de la región sombreada.

Pregunta 14: Dibujar la gráfica de la ecuación . Además, encuentra el área del triángulo formado por la línea y los ejes de coordenadas.

Pregunta 15: Dibuja la gráfica de y = | x |.

Pregunta 16: Dibuja la gráfica de y = | x | + 2.

Pregunta 17: Dibuja las gráficas de las siguientes ecuaciones lineales en el mismo papel cuadriculado:

Encuentra las coordenadas de los vértices del triángulo formado por las dos líneas rectas y el área delimitada por estas líneas y el eje x.

Pregunta 18: Dibuja las gráficas de las ecuaciones lineales 4x − 3y + 4 = 0 y 4x + 3y −20 = 0. Encuentra el área delimitada por estas líneas y el eje x.

Pregunta 19: La trayectoria de un tren A viene dada por la ecuación 3x + 4y − 12 = 0 y la trayectoria de otro tren B viene dada por la ecuación 6x + 8y − 48 = 0. Representa gráficamente esta situación.

Pregunta 21: Aarushi conducía un automóvil con una velocidad uniforme de 60 km/h. Dibujar gráfica distancia-tiempo. A partir de la gráfica, encuentre la distancia recorrida por Aarushi en

Deja una respuesta Cancelar la respuesta

Pregunta 11: Dibuja la gráfica de la ecuación 2x + 3y = 12. A partir de la gráfica, encuentra las coordenadas del punto:

Pregunta 13: Dibuja la gráfica de la ecuación 2x + y = 6. Sombrea la región delimitada por la gráfica y los ejes de coordenadas. Además, encuentre el área de la región sombreada.

Pregunta 14: Dibujar la gráfica de la ecuación $\frac{x}{3}+\frac{y}{4}=1$ . Además, encuentra el área del triángulo formado por la línea y los ejes de coordenadas.