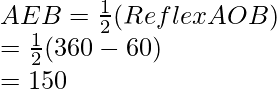Clase 9 Soluciones RD Sharma – Capítulo 16 Círculos – Ejercicio 16.4

Pregunta 1. En la Fig., O es el centro del círculo. Si ∠APB∠APB= 50°, encuentre ∠AOB y ∠OAB.

Solución:

∠APB=50°

Por teorema de medida de grado

∠AOB=2APB

∠APB=2*50°=100°

desde OA=OB [Radio del círculo]

Entonces ∠OAB=∠OBA [Ángulos opuestos a lados iguales]

Sea ∠OAB=x

En △OAb, por propiedad de suma de ángulos  

∠OAB+∠OBA+∠AOB=180°

x+x+100°=180°

2x=180°-100°

2x=80°

x=40°

∠OAB=∠OBA=40°

Pregunta 2. En la Fig., se da que O es el centro del círculo y ∠AOC = 150°. Encuentra ∠ABC.

Solución:

∠AOC = 150°

∠AOC+reflejo ∠AOC = 360° [ángulo complejo]

150°+reflejo ∠AOC = 360°

reflejo ∠AOC=210°

2∠ABC=210° [Teorema de la medida en grados]

∠ABC=210°/2=105°

Pregunta 3. En la Fig., O es el centro del círculo. Encuentre ∠BAC.

Solución:

Tenemos ∠AOB=80°

Y ∠AOC=110°

Por lo tanto, ∠AOB+∠AOC+∠BOC=360° [ángulo completo]

80+100+∠BOC=360°

∠BOC=360°-80°-110°

∠BOC=70°

Por teorema de medida de grado

∠BOC=2∠BAC

170=2∠BAC

∠BAC=170°/2=85°

Pregunta 4. Si O es el centro del círculo, encuentra el valor de x en cada una de las siguientes figuras.

Solución:

i)

∠AOC=135°

∠AOC+BOC=185° [Par de ángulos lineales]

135°+∠BOC=180°

∠BOC=180°-135°=45°

Por teorema de medida de grado

∠BOC=2∠COB

45 = 2x

x=45°/2=22\frac{1}{2}    

ii)

Tenemos  

∠ABC=40°

∠ACB=90° [Ángulo en semicírculo]

En △ABC, por propiedad de suma de ángulos  

∠CAB+∠ACB+∠ABC=180°

∠CAB+90°+40°=180°

∠CAB=180°-90°-40°

∠CAB=50°

Ahora,

∠CDB=∠CAB [El ángulo es el mismo en el segmento]

x=50°

iii)

Tenemos,

∠AOC=120°

Por teorema de medida de grado

∠AOC=2∠APC

120°=2∠APC

∠APC=120°/2=60

∠APC+∠ABC=180° [Ángulos opuestos de cuadriláteros cíclicos]

60°+∠ABC=180°

∠ABC=180°-60°

∠ABC=120°

∠ABC+∠DBC=180° [Par de ángulos lineales]

120°+x=180°

x=180°-120°=60°

iv)

Tenemos  

∠CDB=65°

∠ABC+∠CBD=180° [Par de ángulos lineales]

∠ABC=65°=180°

∠ABC=180°-65°=115°

reflejo ∠AOC=2∠ABC [Por el teorema de la medida en grados]

x=2*115°

x=230°

v)

Tenemos,

∠OAB=35°

Entonces, ∠OBA=∠OAB=35° [Ángulos opuestos a radios iguales]

En △AOB, por propiedad de suma de ángulos

∠AOB+∠OAB+∠OBA=180°

∠AOB+35°+35°=180°

∠AOB=180°-35°=110°

∠AOB+reflejo ∠AOB=360° [ángulo complejo]

110+reflejo∠AOB=360°

reflejo∠AOB=360°-110°=250°

Por grado medir teorema reflejo∠AOB=2∠ACB

250°=2x

x=250°/2=125°

vi)

Tenemos,

∠AOB=60

Por grado medir teorema reflejo

∠AOB=2∠ACB

60=2∠ACB

∠ACB=60°/2=30° [Ángulo opuesto a radios iguales]

x=30°

viii)

Tenemos,

∠BAC=50° y ∠DBC=70°

∠BDC=∠BAC=50° [Ángulo en el mismo segmento]

En △BDC, por propiedad de suma de ángulos  

∠BDC+∠BCD+∠DBC=180°

50°+x+70°=180°

x=180°-50°-70°=60°

viii)

Tenemos,

∠DBO=40° y ∠DBC=90° ——-[Ángulo en un semicírculo]

∠DBO+∠OBC=90°

40°+∠OBC=90°

∠OBC=90°-40°=50°

Por teorema de medida de grado

∠AOC=∠OBC

x=2*50°=100°

ix)

En ∆DAB, por propiedad de suma de ángulos  

∠ADB+∠DAB+∠ABD=180°

32°+∠DAB+50°=180°

∠DAB=180°-32°-50°

∠DAB=98°

Ahora,  

∠OAB+∠DCB=180° [ángulo opuesto del cuadrilátero cíclico]

98°+x=180°

x=180°-98°=82°

X)

Tenemos,

∠BAC=35°

∠BDC=∠BAC=35° [Ángulo en el mismo segmento]

En ∆BCD, por propiedad de la suma de ángulos

∠BDC+∠BCD+∠DBC=180°

35°+x+65°=180°

x=180°-35°-65°=80°

xi)

Tenemos,

∠ABD=40°

∠ACD=∠ABD=40° [Ángulo en el mismo segmento]

En ∆PCD, por propiedad de suma de ángulos

∠PCD+∠CPO+∠PDC=180°

40°+110°+x=180°

x=180°-150°

x=30°

xi)

Dado que,

∠BAC=52°

Entonces ∠BDC=∠BAC=52° [Ángulo en el mismo segmento]

Dado que OD=OC

Entonces ∠ODC=∠OCD [Ángulo opuesto a radios iguales]

x=52°

Pregunta 5. O es el circuncentro del triángulo ABC y OD es perpendicular a BC. Demuestra que ∠BOD = ∠A.

Solución:

Tenemos que probar que ∠BOD=∠A

ya que, circun centro es la intersección de la bisectriz perpendicular de cada lado del triángulo. Ahora según la figura A,B,C son los vértices de ∆ABC

En ∆BOC, OD es la bisectriz perpendicular de BC.

Entonces, BD = CD

OB=OC ——–(Radio del mismo círculo)

Y,

OD=OD —–[común]

Por lo tanto,

∆BDO≅∆CDO (criterio de concurrencia SSS)

∠BOD=∠COD (por cpct)

Sabemos que el ángulo formado por cualquier cuerda del círculo en el centro es el doble del ángulo formado en la circunferencia por la misma cuerda

Por lo tanto,

∠BAC=\frac{1}{2} ∠BOC

∠BAC=\frac{1}{2}*2∠DBO

∠BAC=∠DBO

Por lo tanto,

∠DBO=∠A

Pregunta 6. En la Fig., O es el centro del círculo, BO es la bisectriz de ∠ABC. Demuestre que AB = AC.

Solución:

Dado, BO es la bisectriz de ∠ABC

Para probar: AB=BC

Prueba: Dado que BO es la bisectriz de ∠ABC.

Entonces, ∠ABO=∠CBO —-(i)

Ya que, OB=OA [Radio del círculo]

Entonces, ∠ABO=∠DAB ——–(ii) [ángulos opuestos a lados iguales]

Dado que OB=OC [Radio del círculo]

Entonces, ∠OAB=∠OCB ——–(iii) [ángulos opuestos a lados iguales]

comparar las ecuaciones (i), (ii) y (iii)

∠OAB=∠OCB ——-(iv)  

En ∆OAB y ∆OCB

∠OAB=∠OCB [De(iv)]

∠OBA=∠OBC [Dado]

OB=OB [común]

Después

∆OAB≅∆OCB [Por condición AAS]

Por lo tanto, AB=BC [CPCT]

Pregunta 7. En la Fig., O es el centro del círculo, prueba que ∠x = ∠y + ∠z.

Solución:

Tenemos,

∠3=∠4 [Ángulos en el mismo segmento]

∠x=2∠3 [Por el teorema de la medida en grados]

∠x=∠3+∠3⇒∠x=∠3+∠4 ——–(i) [∠3=ángulo 4]

Pero ∠y=∠3+∠1 [Por la propiedad del ángulo exterior]

⇒∠3=∠y-∠1 —-(ii)

de (i) y (ii)

∠x=∠y-∠1+∠4

∠x=∠y+∠4-∠1

∠x=∠y+∠z+∠1-∠1 [Por propiedad del ángulo exterior]

∠x=∠y+∠z

Pregunta 8. En la figura, O y O’ son centros de dos círculos que se cortan en B y C. ACD es una línea recta, encuentra x.

Solución:

Por teorema de medida de grado

∠AOB=2∠ACB

130°=2∠ACB⇒∠ACB=130°/2=65

∠ACB+∠BCD=180° [Par de ángulos lineales]

65°+∠BCD=180°

∠BCD=180-65=115

Por teorema de medida de grado

reflejo∠BOD=2∠BCD

reflejo∠DBO=2*115°=230°

Ahora, reflex∠BOD+∠BOD=360° [ángulo complejo]

230°+x=360°

x=360°-230°

x=130°

Pregunta 9. En la Fig., O es el centro de un círculo y PQ es un diámetro. Si ∠ROS = 40°, encuentre ∠RTS.

Solución:

Como PQ es el diámetro

Después,

∠PRQ=90° [Ángulo en semicírculo]

∠PRQ+∠TRQ=180° [Par de ángulos lineales]

90+∠TRQ=180

∠TRQ=180°-90°=90°

Por teorema de medida de grado

∠ROS=2∠RQS

40=2∠RQS

∠RQS=40°/2=20°

En ∆RQT, por propiedad de suma de ángulos

∠RQT+∠QRT+∠RTS=180°

20°+90°+∠RTS=180°

Pregunta 10. En la figura, si ∠ACB = 40°, ∠DPB = 120°, encuentre ∠CBD.

Solución:

Tenemos,

∠ACB=40°; ∠DPB=120°

∠APB=∠DCB=40° [Ángulo en el mismo segmento]

En ∆POB, por propiedad de suma de ángulos

∠PDB+∠PBD+∠BPD=180°

40+∠PBD+120°=180°

∠PBD=180°-40°-120°

∠PBD=20°

∠CDB=20°

Pregunta 11. Una cuerda de un círculo es igual al radio del círculo. Encuentre el ángulo subtendido por la cuerda en un punto del arco menor y también en un punto del arco mayor.

Solución:

Construcción: O es el centro y r es el radio y dado que la cuerda es igual al radio del círculo.

Ahora en ∆AOB tenemos

AO=OB=BA (Se da que la cuerda es igual al radio de la circunferencia)

entonces, ∆AOB es un triángulo equilátero

∠AOB=60°

Entonces, ∠AOB=2∠ADB (El ángulo subtendido por un arco de círculo en el centro es el doble del ángulo subtendido por él en cualquier punto del resto del círculo)

Entonces ∠ADB=30°

Asi que,

Por lo tanto,

∠ADB=30° y ∠AEB=150°