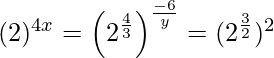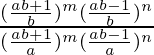Pregunta 12. Determinar (8x) x , si 9 x+2 = 240 + 9 x .
Solución:
Tenemos,
=> 9x+2 = 240 + 9x
=> 9x+2 − 9x = 240
=> 9 x (9 2 − 1) = 240
=> 9 x = 240/80
=> 3 2x = 3
=> 2x = 1
=> x = 1/2
Por lo tanto, (8x) x = [8 × (1/2)] 1/2
= 4 1/2
= 2
Pregunta 13. Si 3 x+1 = 9 x−2 , encuentra el valor de 2 1+x .
Solución:
Tenemos,
=> 3x+1 = 9x−2
=> 3 x+1 = (3 2 ) x−2
=> 3x+1 = 3 2x−4
=> x + 1 = 2x − 4
=> x = 5
Por lo tanto, 2 1+x = 2 1+5
= 2 6
= 64
Pregunta 14. Si 3 4x = (81) −1 y (10) 1/y = 0.0001, encuentre el valor de 2 −x+4y .
Solución:
Se nos da,
=> 3 4x = (81) −1
=> 3 4x = (3 4 ) −1
=> 3 4x = (3) −4
=> 4x = −4
=> x = −1
Y también, (10) 1/y = 0.0001
=> (10) 1/año = (10) −4
=> 1/año = −4
=> y = −1/4
Por lo tanto, 2 −x+4y = 2 1+4(−1/4)
= 2 1−1
= 1
Pregunta 15. Si 5 3x = 125 y 10 y = 0.001. Encuentre x e y.
Solución:
Se nos da,
=> 5 3x = 125
=> 5 3x = 5 3
=> 3x = 3
=>x=1
Además, (10) y = 0.001
=> 10 y = 10 −3
=> y = −3
Por lo tanto, el valor de x es 1 y el valor de y es -3.
Pregunta 16. Resuelve las siguientes ecuaciones:
(yo) 3x+1 = 27 × 3 4
Solución:
Tenemos,
=> 3x+1 = 27 × 3 4
=> 3x+1 = 3 3 × 3 4
=> 3x+1 = 3 7
=> x + 1 = 7
=> x = 6
(ii) ![Rendered by QuickLaTeX.com 4^{2x}=\left(\sqrt[3]{16}\right)^{\frac{-6}{y}}=(\sqrt{8})^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e4db93522d462459f93ca4538e51de9b_l3.png)
Solución:
Tenemos,
=>
=>
=>
=>
=> 4x = −8/y = 3
=> x = 3/4 y y = −8/3
(iii) 3 x−1 × 5 2y−3 = 225
Solución:
Tenemos,
=> 3 x−1 × 5 2y−3 = 225
=> 3 x−1 × 5 2y−3 = 3 2 × 5 2
=> x − 1 = 2 y 2y − 3 = 2
=> x = 3 y 2y = 5
=> x = 3 y y = 5/2
(iv) 8 x+1 = 16 y+2 y (1/2) 3+x = (1/4) 3y
Solución:
Tenemos,
=> 8x+1 = 16y+2
=> (2 3 ) x+1 = (2 4 ) y+2
=> 2 3x+3 = 2 4y+8
=> 3x + 3 = 4y + 8 . . . . (1)
Además, (1/2) 3+x = (1/4) 3y
=> (1/2) 3+x = [(1/2) 2 ] 3y
=> (1/2) 3+x = (1/2) 6y
=> 3 + x = 6y
=> x = 6y – 3 . . . . (2)
Poniendo (2) en (1), obtenemos,
=> 3(6y − 3) + 3 = 4y + 8
=> 18y − 9 + 3 = 4y + 8
=> 14 años = 14
=> y = 1
Poniendo y = 1 en (2), obtenemos,
x = 6(1) − 3 = 6 − 3 = 3
Por lo tanto, el valor de x es 1 y el valor de y es -3.
(v) 4 x−1 × (0,5) 3−2x = (1/8) x
Solución:
Tenemos,
=> 4x −1 × (0.5) 3−2x = (1/8) x
=> (2 2 ) x−1 × (1/2) 3−2x = [(1/2) 3 ] x
=> 2 2x−2 × 2 2x−3 = 2 −3x
=> 2 2x−2+2x−3 = 2 −3x
=> 2 4x−5 = 2 −3x
=> 4x − 5 = −3x
=> 7x = 5
=> x = 5/7
(vi) 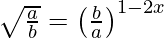
Solución:
Tenemos,
=>
=>
=> 1/2 = 2x − 1
=> 2x = 3/2
=> x = 3/4
Pregunta: 17. Si ayb son primos positivos distintos tales que, ![Rendered by QuickLaTeX.com \sqrt[3]{a^6b^{-4}}=a^xb^{2y}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cbe7ef4d0a788a4bf5d750098215cd64_l3.png) encuentre x e y.
encuentre x e y.
Solución:
Tenemos,
=>
=> (un 6 segundo −4 ) 1/3 = un x segundo 2y
=> un 6/3 segundo −4/3 = un x segundo 2y
=> un 2 segundo −4/3 = un x segundo 2y
=> x = 2 y 2y = −4/3
=> x = 2 y y = −2/3
Pregunta 18. Si a y b son primos positivos diferentes tales que,
(i) 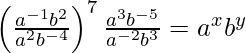 , encuentre x e y.
, encuentre x e y.
Solución:
Tenemos,
=>
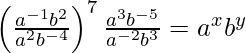
=> (a −1−2 b 2+4 ) 7 ÷ (a 3+2 b −5−3 ) = a x b y
=> (un −3 segundo 6 ) 7 ÷ (un 5 segundo −8 ) = un X segundo y
=> (un −21 segundo 42 ) ÷ (un 5 segundo −8 ) = un X segundo y
=> (un −21−5 segundo 42 +8 ) = un x segundo y
=> (un −26 segundo 50 ) = un x segundo y
=> x = −26, y = 50
(ii) (a + b) −1 (a −1 + b −1 ) = a x b y , encuentre x+y+2.
Solución:
Tenemos,
=> (a + b) −1 (a −1 + b −1 ) = a x b y
=>
= un x segundo y
=>
= un x segundo y
=> 1/ab = a x b y
=> un −1 segundo −1 = un X segundo y
=> x = −1 y y = −1
Entonces, x+y+2 = −1−1+2 = 0.
Pregunta 19. Si 2 x × 3 y × 5 z = 2160, encuentra x, y y z. Por lo tanto, calcule el valor de 3 x × 2 −y × 5 −z .
Solución:
Se nos da,
=> 2 x × 3 y × 5 z = 2160
=> 2 x × 3 y × 5 z = 2 4 × 3 3 × 5 1
=> x = 4, y = 3, z = 1
Por lo tanto, 3 x × 2 −y × 5 −z = 3 4 × 2 −3 × 5 −1
= (81) (1/8) (1/5)
= 81/40
Pregunta 20. Si 1176 = 2 a × 3 b × 7 c , encuentra los valores de a, b y c. Por lo tanto, calcule el valor de 2 a × 3 b × 7 -c como una fracción.
Solución:
Se nos da,
=> 1176 = 2 un × 3 segundo × 7 c
=> 2 3 × 3 1 × 7 2 = 2a × 3b × 7c
=> a = 3, b = 1, c = 2
Por lo tanto, 2 a × 3 b × 7 −c = 2 3 × 3 1 × 7 −2
= (8) (3) (1/49)
= 24/49
Pregunta 21. Simplifica
(i) 
Solución:
Tenemos,
=
= (x a+b−c ) a−b (x b+c−a ) b−c (x c+a−b ) c−a
=
=
= x 0
= 1
(ii) ![Rendered by QuickLaTeX.com \sqrt[lm]{\frac{x^l}{x^m}}×\sqrt[mn]{\frac{x^m}{x^n}}×\sqrt[nl]{\frac{x^n}{x^l}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5999c7417ca8e24471478ce989cfe1a3_l3.png)
Solución:
Tenemos,
=>
![Rendered by QuickLaTeX.com \sqrt[lm]{\frac{x^l}{x^m}}×\sqrt[mn]{\frac{x^m}{x^n}}×\sqrt[nl]{\frac{x^n}{x^l}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d33ca8f7d224eec85584481f585c8c8_l3.png)
=>
=>
=>
=>
=>
=> x0
= 1
Pregunta 22. Demuestre que 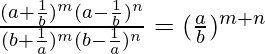 .
.
Solución:
Tenemos,
IZQ =
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 23. (i) Si a = x m+n y l , b = x n+l y m y c = x l+m y n , demuestre que a m−n b n−l c l−m = 1 .
Solución:
Dado, a = x m+n y l , b = x n+l y m y c = x l+m y n .
Tenemos,
LHS = a m−n b n−l c l−m
= (x metro+n y l ) metro−n (x norte+l y metro ) norte−l (x l+m y norte ) l−m
=
=
= x 0 y 0
= 1
= lado derecho
Por lo tanto probado.
(ii) Si x = a m+n , y = a n+l y z = a l+m , demuestre que x m y n z l = x n y l z m .
Solución:
Dado, x = a m+n , y = a n+l y z = a l+m .
Tenemos,
LHS = x metro y norte z l
= (un metro+n ) metro (un norte+l ) norte (un l+m ) l
=
=
= (un metro+n ) norte ( un norte+l ) l (un l+m ) metro
= x norte y l z metro
= lado derecho
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
![Rendered by QuickLaTeX.com (2^2)^{2x}=\left(\sqrt[3]{2^4}\right)^{\frac{-6}{y}}=(\sqrt{2^3})^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2cab1ad8c40b06925ea7a539c7f8024c_l3.png)