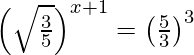Pregunta 1. Suponiendo que x, y, z son números reales positivos, simplifica cada uno de los siguientes:
(i) 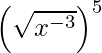
Solución:
Tenemos,
=
=
=
=
(ii) 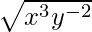
Solución:
Tenemos,
=
=
=
(iii) 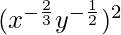
Solución:
Tenemos,
=
=
=
(iv) 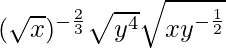
Solución:
Tenemos,
=
=
=
=
=
(v) ![Rendered by QuickLaTeX.com \sqrt[5]{243x^{10}y^5z^{10}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a93a1c135db47a548f476a25c7a9bd34_l3.png)
Solución:
Tenemos,
=
=
=
= 3 x 2 yz 2
(vi) 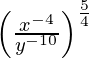
Solución:
Tenemos,
=
=
=
=
(vii) 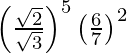
Solución:
Tenemos,
=
=
=
=
Pregunta 2. Simplifica
(i) 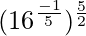
Solución:
Tenemos,
=
=
=
=
(ii) ![Rendered by QuickLaTeX.com \sqrt[5]{(32)^{-3}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-44358da979b65226f5e3f2b680d053b6_l3.png)
Solución:
Tenemos,
=
=
= 2 −3
=
(iii) ![Rendered by QuickLaTeX.com \sqrt[3]{(343)^{-2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3f7df08e4ea13ce4b7403747a00ca0d8_l3.png)
Solución:
Tenemos,
=
=
= 7 −2
=
(iv) 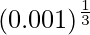
Solución:
Tenemos,
=
=
=
= 0,1
(v) 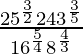
Solución:
Tenemos,
=
=
=
=
=
(vi) 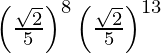
Solución:
Tenemos,
=
=
=
=
=
(vii) 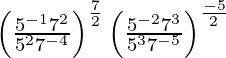
Solución:
Tenemos,
=
=
=
= 5 2 × 7
= 175
Pregunta 3. Demuestra que
(i) ![Rendered by QuickLaTeX.com (\sqrt{3×5^{-3}}÷\sqrt[3]{3^{-1}}\sqrt{5})×\sqrt[6]{3×5^6}=\frac{3}{5}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bb68981e6aa90601906cfa71ecffbed7_l3.png)
Solución:
Tenemos,
IZQ =
=
=
=
=
=
=
= lado derecho
Por lo tanto probado.
(ii) 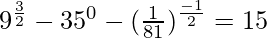
Solución:
Tenemos,
IZQ =
=
=
= 27 − 3 − 9
= 15
= lado derecho
Por lo tanto probado.
(iii) 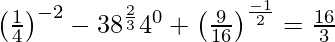
Solución:
Tenemos,
IZQ =
=
=
=
=
= lado derecho
Por lo tanto probado.
(iv) 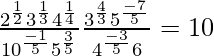
Solución:
Tenemos,
IZQ =
=
=
=
=
= 2 × 1 × 5
= 10
= lado derecho
Por lo tanto probado.
(v) 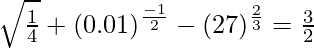
Solución:
Tenemos,
IZQ =
=
=
=
= lado derecho
Por lo tanto probado.
(vi) 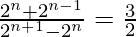
Solución:
Tenemos,
IZQ =
=
= 1 +
=
= lado derecho
Por lo tanto probado.
(vii) ![Rendered by QuickLaTeX.com \left(\frac{64}{125}\right)^{\frac{-2}{3}}+\frac{1}{(\frac{256}{625})^{\frac{1}{4}}}+\left(\frac{\sqrt{25}}{\sqrt[3]{64}}\right)^0=\frac{61}{16}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f359259b7bc3551a127fc7a5f84593ec_l3.png)
Solución:
Tenemos,
IZQ =
=
=
=
= lado derecho
Por lo tanto probado.
(viii) ![Rendered by QuickLaTeX.com \frac{3^{-3}×6^2×\sqrt{98}}{5^2×\sqrt[3]{\frac{1}{25}}×(15)^{\frac{-4}{3}}×3^{\frac{1}{3}}}=28\sqrt{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a35c7a2806ef269a818d13a8345c6ce9_l3.png)
Solución:
Tenemos,
IZQ =
=
=
=
=
= 28√2
= lado derecho
Por lo tanto probado.
(ix) 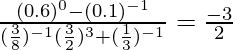
Solución:
Tenemos,
IZQ =
=
=
=
=
= lado derecho
Por lo tanto probado.
Pregunta 4. Demuestra que
(i) 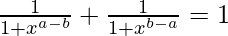
Solución:
Tenemos,
IZQ =
=
=
=
= 1
= lado derecho
Por lo tanto probado.
(ii) ![Rendered by QuickLaTeX.com \left[\left(\frac{x^{a(a-b)}}{x^{a(a+b)}}\right)÷\left(\frac{x^{b(b-a)}}{x^{b(b+a)}}\right)\right]^{a+b}=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3822dfe3c4fb018c9f455d315ed67219_l3.png)
Solución:
Tenemos,
IZQ =
=
=
= [x -2ab-(-2ab) ] a+b
= [x 0 ] a+b
= x 0
= 1
= lado derecho
Por lo tanto probado.
(iii) 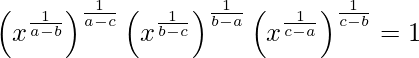
Solución:
Tenemos,
IZQ =
=
=
=
= x 0
= 1
= lado derecho
Por lo tanto probado.
(iv) 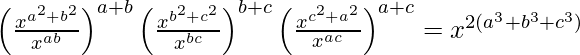
Solución:
Tenemos,
IZQ =
=
=
=
= lado derecho
Por lo tanto probado.
(v) (x a-b ) a+b (x b-c ) b+c (x c-a ) c+a = 1
Solución:
Tenemos,
IZQ = (x a-b ) a+b (x b-c ) b+c (x c-a)c+a
=
=
= x 0
= 1
= lado derecho
Por lo tanto probado.
(vi) ![Rendered by QuickLaTeX.com \left[(x^{a-a^{-1}})^{\frac{1}{a-1}}\right]^{\frac{a}{a+1}}=x](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a22fff441eaff54b0f93c5e824bc1f24_l3.png)
Solución:
Tenemos,
IZQ =
=
=
= x
= lado derecho
Por lo tanto probado.
(vii) ![Rendered by QuickLaTeX.com \left[\frac{a^{x+1}}{a^{y+1}}\right]^{x+y}\left[\frac{a^{y+2}}{a^{z+2}}\right]^{y+z}\left[\frac{a^{z+3}}{a^{z+3}}\right]^{x+z}=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c697294879397f74f8c4746990709769_l3.png)
Solución:
Tenemos,
IZQ =
= (a x-y ) x+y (a y-z ) y+z (a x-z ) x+z
=
=
= un 0
= 1
= lado derecho
Por lo tanto probado.
(viii) ![Rendered by QuickLaTeX.com \left[\frac{3^a}{3^b}\right]^{a+b}\left[\frac{3^b}{3^c}\right]^{b+c}\left[\frac{3^c}{3^a}\right]^{c+a}=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9e7429ec05818b8faf9dc1ea9a99c0de_l3.png)
Solución:
Tenemos,
IZQ =
= (3 a-b ) a+b (3 b-c ) b+c (3 c-a ) c+a
=
=
= 3 0
= 1
= lado derecho
Por lo tanto probado.
Pregunta 5. Si 2 x = 3 y = 12 z , demuestre que 1/z = 1/y + 2/x.
Solución:
Se nos da,
=> 2 x = 3 y = 12 z = k (digamos)
Entonces, obtenemos,
=> 12 = k 1/z
=> 2 × 3 × 2 = k 1/z
=> 2 2 × 3 = k 1/z
=> (k 1/x ) 2 × (k) 1/y = k 1/z
=> (k) 2/x × (k) 1/y = k 1/z
=>
= k 1/z
=> 2/x + 1/y = 1/z
Por lo tanto probado.
Pregunta 6. Si 2 x = 3 y = 6 −z , demuestra que 1/x + 1/y + 1/z = 0.
Solución:
Se nos da,
=> 2 x = 3 y = 6 −z = k (digamos)
Entonces, obtenemos,
=> 6 = k -1/z
=> (2 × 3) = k -1/z
=> k 1/x × k 1/y = k -1/z
=>
= k -1/z
=> 1/x + 1/y = −1/z
=> 1/x + 1/y + 1/z = 0
Por lo tanto probado.
Pregunta 7. Si a x = b y = c z y b 2 = ac, entonces demuestre que y = 2zx/(z+x).
Solución:
Se nos da,
=> a x = b y = c z = k (digamos)
=> un = k 1/x , segundo = k 1/y , c = k 1/z
Nos dan, b 2 = ac
=> (k 1/y ) 2 = k 1/x × k 1/z
=> k 2/año =
=> 2/y = 1/x + 1/z
=> 2/y = (x+z)/xz
=> y = 2zx/(z+x)
Por lo tanto probado.
Pregunta 8. Si 3 x = 5 y = (75) z , demuestre que z = xy/(2x+y).
Solución:
Se nos da,
=> 3 x = 5 y = (75) z = k (digamos)
Entonces, obtenemos,
=> 75 = k 1/z
=> 3 × 5 2 = k 1/z
=> (k) 1/x × (k 1/y ) 2 = k 1/z
=> (k) 1/x × (k) 2/y = k 1/z
=>
= k 1/z
=> 1/x + 2/y = 1/z
=> (2x+y)/xy = 1/z
=> z = xy/(2x+y)
Por lo tanto probado.
Pregunta 9. Si (27) x = 9/3 x , encuentra x.
Solución:
Se nos da,
=> (27) x = 9/3 x
=> (3 3 ) x = 3 2 /3 x
=> 3 3x = 3 2−x
=> 3x = 2 − x
=> 4x = 2
=> x = 2/4
=> x = 1/2
Pregunta 10. Encuentra los valores de x en cada uno de los siguientes:
(i) 2 5x ÷ 2x = ![Rendered by QuickLaTeX.com \sqrt[5]{2^{20}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f68b12dd6f1ec5654a08bb1e94601d1a_l3.png)
Solución:
Tenemos,
=> 2 5x ÷ 2x =
=> 2 5x−x =
=> 2 4x = 2 4
=> 4x = 4
=> x = 1
(ii) (2 3 ) 4 = (2 2 ) x
Solución:
Tenemos,
=> (2 3 ) 4 = (2 2 ) x
=> 2 12 = 2 2x
=> 2x = 12
=> x = 6
(iii) 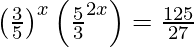
Solución:
Tenemos,
=>
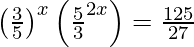
=>
=>
=>
=>
=> x = 3
(iv) 5 x−2 × 3 2x−3 = 135
Solución:
Tenemos,
=> 5 x−2 × 3 2x−3 = 135
=> 5 x−2 × 3 2x−3 = 5 × 27
=> 5 x−2 × 3 2x−3 = 5 1 × 3 3
=> x − 2 = 1 y 2x − 3 = 3
=> x = 3
(v) 2x−7 × 5x−4 = 1250
Solución:
Se nos da,
=> 2 x−7 × 5 x−4 = 1250
=> 2 x−7 × 5 x−4 = 2 × 625
=> 2 x−7 × 5 x−4 = 2 × 5 4
=> x − 7 = 1 y x − 4 = 4
=> x = 8
(vi) ![Rendered by QuickLaTeX.com (\sqrt[3]{4})^{2x+\frac{1}{2}}=\frac{1}{32}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1b8dbb385737e9b866b63645faba643_l3.png)
Solución:
Tenemos,
=>
=>
=>
=> 4x/3 + 1/3 = −5
=> 4x +1 = −15
=> 4x = −16
=> x = −4
(vii) 5 2x+3 = 1
Solución:
Tenemos,
=> 5 2x+3 = 1
=> 5 2x+3 = 5 0
=> 2x + 3 = 0
=> 2x = −3
=> x = −3/2
(viii) 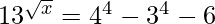
Solución:
Tenemos,
=>
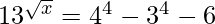
=>
= 256 − 81 − 6
=>
= 169
=>
=> √x = 2
=> x = 4
(ix) 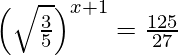
Solución:
Tenemos,
=>
=>
=>
=> (x+1)/2 = −3
=> x + 1 = −6
=> x = −7
Pregunta 11. Si x = 2 1/3 + 2 2/3 , demuestra que x 3 − 6x = 6.
Solución:
Dado, x = 2 1/3 + 2 2/3
Por lo tanto, x 3 = (2 1/3 ) 3 + (2 2/3 ) 3 + 3(2 1/3 )(2 2/3 )(2 1/3 + 2 2/3 )
=> x 3 = (2 1/3 )3 + (2 2/3 ) 3 + 3(2 1/3 )(2 2/3 )(x)
=> x3 = 2 + 4 + 3(2)(x)
=> x3 = 6 + 6x
=> x3 − 6x = 6
Por lo tanto probado.
Publicación traducida automáticamente
Artículo escrito por gurjotloveparmar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
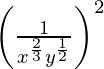
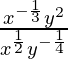
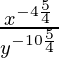
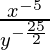
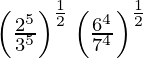
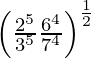
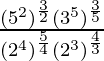
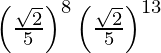
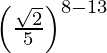
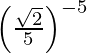
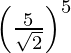
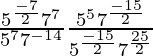
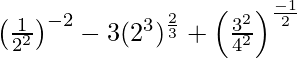
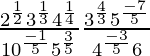
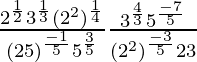
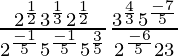
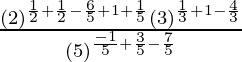
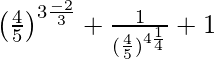
![Rendered by QuickLaTeX.com \frac{3^{-3}×6^2×\sqrt{98}}{5^2×\sqrt[3]{\frac{1}{25}}×(15)^{\frac{-4}{3}}×3^{\frac{1}{3}}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e637addc0eed93605cfbe6a77029e3e0_l3.png)
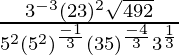
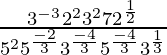
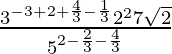
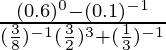
![Rendered by QuickLaTeX.com \left[\left(\frac{x^{a(a-b)}}{x^{a(a+b)}}\right)÷\left(\frac{x^{b(b-a)}}{x^{b(b+a)}}\right)\right]^{a+b}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c250bfac90c1fafbf8d0286a2f486f7c_l3.png)
![Rendered by QuickLaTeX.com \left[\left(\frac{x^{a^2-ab}}{x^{a^2+ab}}\right)÷\left(\frac{x^{b^2-ab}}{x^{b^2+ab}}\right)\right]^{a+b}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6105072b555f60736fdbde38e0cff6c2_l3.png)
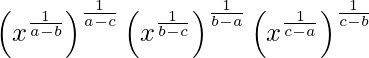
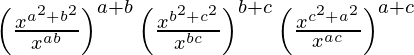
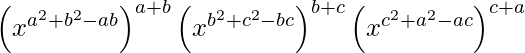
![Rendered by QuickLaTeX.com \left[(x^{a-a^{-1}})^{\frac{1}{a-1}}\right]^{\frac{a}{a+1}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d4b6c7ff42b26c121328b5842f1ccab1_l3.png)
![Rendered by QuickLaTeX.com \left[x^{\frac{a(a-a^{-1})}{a^2-1}}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-36940ea397cfcf6ace7d6bbd080b1c3d_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{a^{x+1}}{a^{y+1}}\right]^{x+y}\left[\frac{a^{y+2}}{a^{z+2}}\right]^{y+z}\left[\frac{a^{z+3}}{a^{z+3}}\right]^{x+z}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a679ca701be081d04ebabdecdbb0aaf5_l3.png)
![Rendered by QuickLaTeX.com \left[\frac{3^a}{3^b}\right]^{a+b}\left[\frac{3^b}{3^c}\right]^{b+c}\left[\frac{3^c}{3^a}\right]^{c+a}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0fd107ec16141db04d55462b4f1676f9_l3.png)