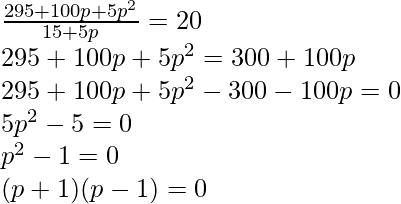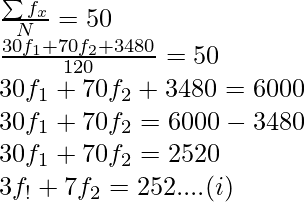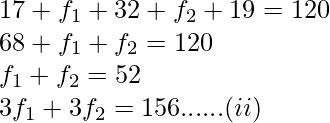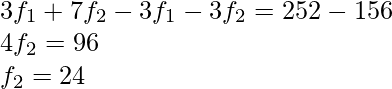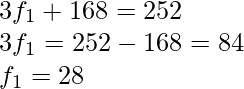Clase 9 RD Sharma Solutions – Capítulo 24 Medidas de Tendencia Central – Ejercicio 24.2

Pregunta 1. Calcula la media de la siguiente distribución:

X:	5	6	7	8	9
F:	4	8	11	14	3

Solución:

X F efectos especiales

5 4 20

6 8 48

7 14 98

8 11 88

9 3 27

norte = 40 $\sum f_x = 281$

Ahora, media = $\overline{x} = \frac{\sum f_x}{N}$

= 281/40

= 7.025

Pregunta 2. Calcula la media de la siguiente distribución:

X:	19	21	23	25	27	29	31
F:	13	15	dieciséis	18	dieciséis	15	13

Solución:

X F efectos especiales

19 13 247

21 15 315

23 dieciséis 368

25 18 450

27 dieciséis 432

29 15 435

31 13 403

norte = 106 $\sum f_x = 2650$

Ahora, media = $\overline{x} = \frac{\sum f_x}{N}$

= 2650/106

= 25

Pregunta 3. La media de los siguientes datos es 20,6. Encuentre el valor de p.

X:	10	15	pags	25	35
F:	3	10	25	7	5

Solución:

X F efectos especiales

10 3 30

15 10 150

pags 25 25p

25 7 175

35 5 175

norte = 50 $\sum f_x = 25p + 530$

Ahora, media = $\overline{x} = \frac{\sum f_x}{N}$

= (25p + 530)/50

Dado,

Media = 20,6

Resolviendo, obtenemos,

20,6 = (25p + 530)/50

25p + 530 = 1030

25p = 1030 − 530 = 500

es decir, p = 20

Pregunta 4. Si la media de los siguientes datos es 15, encuentra p.

X:	5	10	15	20	25
F:	6	pags	6	10	5

Solución:

X F efectos especiales

5 6 30

10 pags 10p

15 6 90

20 10 200

25 5 125

N = p+27 $\sum f_x=10p+445$

Media = $\overline{x} = \frac{\sum f_x}{N}$

= (10p + 445)/(p + 27)

Dar,

Media = 15

Resolviendo, (10p + 445)/(p + 27) = 15

10p + 445 = 15(p + 27)

10p – 15p = 405 – 445 = -40

-5p = -40

es decir, p = 8

Pregunta 5. Halla el valor de p para la siguiente distribución cuya media es 16,6.

X:	8	12	15	pags	20	25	30
F:	12	dieciséis	20	24	dieciséis	8	4

Solución:

X F efectos especiales

8 12 96

12 dieciséis 192

15 20 300

pags 24 24p

20 dieciséis 320

25 8 200

30 4 120

norte = 100 $\sum f_x = 24p + 1228$

Ahora, media = $\overline{x} = \frac{\sum f_x}{N}$

= (24p + 1228)/100

Dado,

Media = 16,6

Resolviendo, (24p + 1228)/100 = 16.6

24p + 1228 = 1660

24p = 1660 – 1228 = 432

p = 432/24

= 18

Pregunta 6. Encuentra el valor faltante de p para la siguiente distribución cuya media es 12.58.

X:	5	8	10	12	pags	20	25
F:	2	5	8	22	7	4	2

Solución:

X F efectos especiales

5 2 10

8 5 40

10 8 80

12 22 264

pags 7 7p

20 4 80

25 2 50

norte = 50 $\sum f_x = 7p + 524$

Media = $\overline{x} = \frac{\sum f_x}{N}$

= (7p + 524)/50

Dado,

Media = 12,58

Resolviendo, (7p + 524)/50 = 12.58

7p + 524 = 12,58 x 50

7p + 524 = 629

7p = 629 – 524 = 105

p = 105/7

= 15

Pregunta 7. Encuentra la frecuencia faltante (p) para la siguiente distribución cuya media es 7.68.

X:	3	5	7	9	11	13
F:	6	8	15	pags	8	4

Solución:

X F efectos especiales

3 6 18

5 8 40

7 15 105

9 pags 9p

11 8 88

13 4 52

norte = pag +41 $\sum f_x = 9p+303$

Media = $\overline{x} = \frac{\sum f_x}{N}$

= (9p + 303)/(p+41)

Dado,

Media = 7,68

Resolviendo obtenemos, (9p + 303)/(p+41) = 7.68

9p + 303 = 7,68 (p + 41)

9p + 303 = 7,68p + 314,88

9p − 7,68p = 314,88 − 303

1,32p = 11,88

es decir, p = (11,881)/(1,32) = 9

Pregunta 8. Encuentra el valor faltante de p para la siguiente distribución cuya media es 12.58.

X:	5	8	10	12	pags	20	25
F:	2	5	8	22	7	4	2

Solución:

X F efectos especiales

5 2 10

8 5 40

10 8 80

12 22 264

pags 7 7p

20 4 80

25 2 50

norte = 50 $\sum f_x =7p + 524$

Dado,

Media = 12,58

=> 7p + 524/50 = 12,58

=> 7p + 524 = 629

=> 7p = 629 – 524

Resolviendo para p, obtenemos,

=> 7p = 105

es decir, p = 105/7 = 15

Pregunta 9. Encuentra la frecuencia faltante (p) para la siguiente distribución cuya media es 7.68.

X:	3	5	7	9	11	13
F:	6	8	15	pags	8	4

Solución:

X F efectos especiales

3 6 18

5 8 40

7 15 105

9 pags 9p

11 8 88

13 4 52

norte = pag + 41 $\sum f_x =9p + 303$

Media = $\overline{x} = \frac{\sum f_x}{N}$

Dado,

Media = 7,68

Ahora,

9p + 303/ (p +41) = 7,68

Resolviendo, obtenemos,

9p + 303 = 7,68 + 314,88

9p-7.68p = 314.88 – 303

1,32p = 11,88

p = 9

Pregunta 10. Encuentra el valor de p, si la media de la siguiente distribución es 20.

X:	15	17	19	20+p	23
F:	2	3	4	5p	6

Solución:

X F efectos especiales

15 2 30

17 3 51

19 4 76

20+p 5p 100p+5p ²

23 6 138

N = 15+5p $\sum f_x = 295+100p+5p^2$

Dado,

Media = 20

Media = $\overline{x} = \frac{\sum f_x}{N}$

$\frac{295+100p+5p^2}{15+5p}=20 \\ 295 + 100p + 5p^2 = 300+100p \\ 295 + 100p + 5p^2 - 300 - 100p = 0 \\ 5p^2 - 5 =0 \\ p^2 -1 =0 \\(p+1)(p-1) = 0$

Si p+1 = 0 o p-1 =0

p=-1

Pregunta 11. Candidatos de cuatro escuelas aparecen en una prueba de matemáticas. Los datos fueron los siguientes:

Escuelas	Nº de Candidatos	Puntuación media
yo	60	75
II	48	80
tercero	No disponible	55
IV	40	50

Si el puntaje promedio de los candidatos de las cuatro escuelas es 66, encuentre el número de candidatos que aparecieron en la escuela III.

Solución:

Supongamos que el número de candidatos en la escuela III es p.

Por lo tanto,

Número total de candidatos en las cuatro escuelas = 60 + 48 + p + 40 = 148 + p

Puntaje promedio de cuatro escuelas = 66

∴Cálculo de la puntuación total de los candidatos = (148 + p) x 66

Ahora,

La nota media de 60 en la escuela I equivale a 75 .

Total en la escuela I = 60 x 75 = 4500

La nota media de 48 en la escuela II equivale a 80 .

Total en la escuela II = 48 x 80 = 3840

En la escuela III, media de p = 55

Total en la escuela III= 55 xp = 55p

y en la escuela IV, media de 40 = 50

Total en la escuela IV = 40 x 50 = 2000

Dado que, el total de los candidatos es 148+p.

También,

Puntuación total = 4500 + 3840 + 55p + 2000 = 10340 + 55p

∴10340 + 55p = (148 + p) x 66 = 9768 + 66p

=> 10340 – 9768 = 66p – 55p

=> 572 = 11p

∴ p = 572/11

Por lo tanto,

El número de candidatos en la escuela III = 52

Pregunta 12. Encuentra las frecuencias que faltan en la siguiente distribución de frecuencias si se sabe que la media de la distribución es 50.

X:	10	30	50	70	90
F:	17	F ₁	32	F ₂	19	totales = 120

Solución:

X F efectos especiales

10 17 170

30 F ₁ 30f ₁

50 32 1600

70 F ₂ 70f ₂

90 19 1710

norte = 120 $\sum f_x = 3480+30f_1 + 70f_2$

Dado,

Media = 50

$\frac{\sum f_x}{N} = 50 \\ \frac{30f_1 + 70f_2 + 3480}{120} = 50 \\ 30f_1 + 70f_2 + 3480 = 6000 \\ 30f_1 + 70f_2 = 6000- 3480 \\ 30f_1 + 70f_2 = 2520 \\ 3f_! + 7f_2 = 252 ....(i)$

Y dado el valor de N = 120

$17 + f_1 + 32+ f_2 + 19 = 120 \\ 68 + f_1 + f_2 = 120 \\ f_1 + f_2 = 52 \\ 3f_1+3f_2 = 156 ......(ii)$

Restando (ii) de (i),

$3f_1+7f_2-3f_1-3f_2 = 252-156 \\ 4f_2 = 96 \\ f_2 = 24$

Sustituyendo f ₂ en (i)

$3f_1 + 168 = 252 \\ 3f_1 = 252-168 = 84 \\ f_1 = 28$

Publicación traducida automáticamente

Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Pregunta 1. Calcula la media de la siguiente distribución:

Pregunta 2. Calcula la media de la siguiente distribución:

Pregunta 3. La media de los siguientes datos es 20,6. Encuentre el valor de p.

Pregunta 4. Si la media de los siguientes datos es 15, encuentra p.

Pregunta 5. Halla el valor de p para la siguiente distribución cuya media es 16,6.

Pregunta 6. Encuentra el valor faltante de p para la siguiente distribución cuya media es 12.58.

Pregunta 7. Encuentra la frecuencia faltante (p) para la siguiente distribución cuya media es 7.68.

Pregunta 9. Encuentra la frecuencia faltante (p) para la siguiente distribución cuya media es 7.68.

Pregunta 10. Encuentra el valor de p, si la media de la siguiente distribución es 20.

Pregunta 11. Candidatos de cuatro escuelas aparecen en una prueba de matemáticas. Los datos fueron los siguientes:

Si el puntaje promedio de los candidatos de las cuatro escuelas es 66, encuentre el número de candidatos que aparecieron en la escuela III.

Pregunta 12. Encuentra las frecuencias que faltan en la siguiente distribución de frecuencias si se sabe que la media de la distribución es 50.

Deja una respuesta Cancelar la respuesta