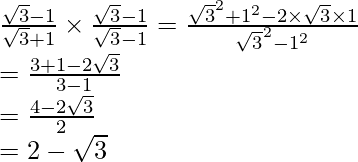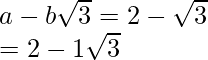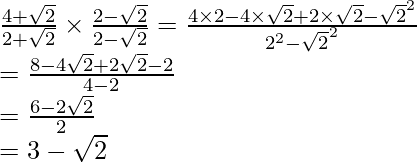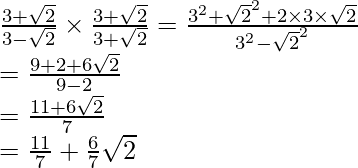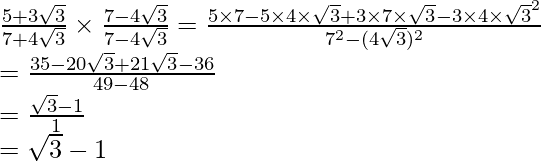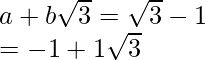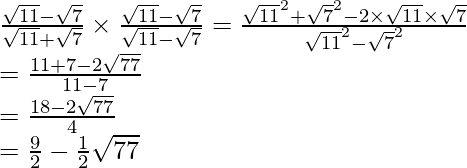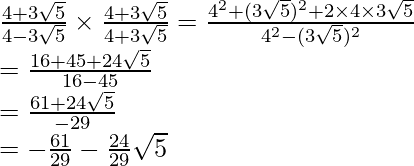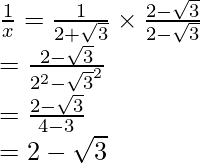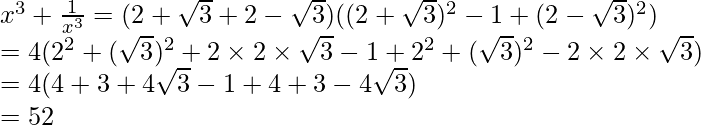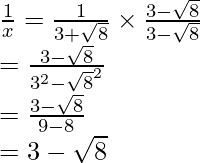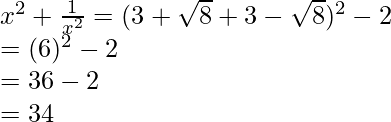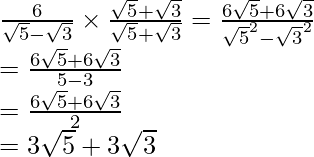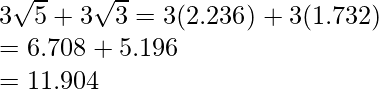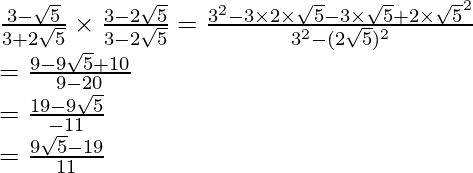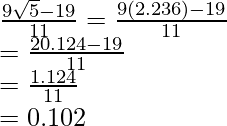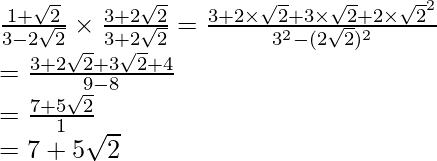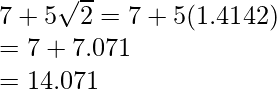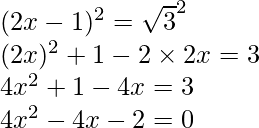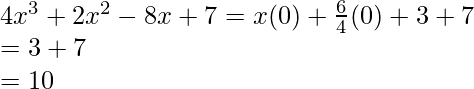Clase 9 RD Sharma Solutions – Capítulo 3 Racionalización – Ejercicio 3.2

Pregunta 6. En cada uno de los siguientes determine los números racionales a y b:

(i) $\frac{\sqrt3-1}{\sqrt3+1}=a-b\sqrt3$

(ii) $\frac{4+\sqrt2}{2+\sqrt2}=n-\sqrt{b}$

(iii) $\frac{3+\sqrt2}{3-\sqrt2}=a+b\sqrt2$

(iv) $\frac{5+3\sqrt3}{7+4\sqrt3}=a+b\sqrt3$

(v) $\frac{\sqrt{11}-\sqrt7}{\sqrt{11}+\sqrt7}=a-b\sqrt{77}$

(vi) $\frac{4+3\sqrt5}{4-3\sqrt5}=a+b\sqrt5$

Solución:

(i) Sabemos que el factor de racionalización para $\sqrt3+1\ is\ \sqrt3-1$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{\sqrt3-1}{\sqrt3+1}\ by\ \sqrt3-1$ , para obtener

$\frac{\sqrt3-1}{\sqrt3+1}\times\frac{\sqrt3-1}{\sqrt3-1}=\frac{\sqrt3^2+1^2-2\times\sqrt3\times1}{\sqrt3^2-1^2}\\ =\frac{3+1-2\sqrt3}{3-1}\\ =\frac{4-2\sqrt3}{2}\\ =2-\sqrt3$

Al igualar términos racionales e irracionales, obtenemos

$a-b\sqrt3=2-\sqrt3\\ =2-1\sqrt3$

Por lo tanto, obtenemos a = 2, b = 1

(ii) Sabemos que el factor de racionalización para $2+\sqrt2\ is\ 2-\sqrt2$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{4+\sqrt2}{2+\sqrt2}\ by\ 2-\sqrt2$ , para obtener

$\frac{4+\sqrt2}{2+\sqrt2}\times\frac{2-\sqrt2}{2-\sqrt2}=\frac{4\times2-4\times\sqrt2+2\times\sqrt2-\sqrt2^2}{2^2-\sqrt2^2}\\ =\frac{8-4\sqrt2+2\sqrt2-2}{4-2}\\ =\frac{6-2\sqrt2}{2}\\ =3-\sqrt2$

Al igualar términos racionales e irracionales, obtenemos

$a-\sqrt{b}=3-\sqrt2$

Por lo tanto, obtenemos a = 3, b = 2

(iii) Sabemos que el factor de racionalización para $3-\sqrt2\ is\ 3+\sqrt2$ . Multiplicaremos numerador y denominador de la expresión dada, para obtener

$\frac{3+\sqrt2}{3-\sqrt2}\times\frac{3+\sqrt2}{3+\sqrt2}=\frac{3^2+\sqrt2^2+2\times3\times\sqrt2}{3^2-\sqrt2^2}\\ =\frac{9+2+6\sqrt2}{9-2}\\ =\frac{11+6\sqrt2}{7}\\ =\frac{11}{7}+\frac{6}{7}\sqrt2$

Al igualar términos racionales e irracionales, obtenemos

$a+b\sqrt2=\frac{11}{7}+\frac{6}{7}\sqrt2$

Por lo tanto, obtenemos a = $\frac{11}7{}$ , b = $\frac{6}{7}$

(iv) Sabemos que el factor de racionalización para $7+4\sqrt3\ is\ 7-4\sqrt3$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{5+3\sqrt3}{7+4\sqrt3}\ by\ 7-4\sqrt3$ , para obtener

$\frac{5+3\sqrt3}{7+4\sqrt3}\times\frac{7-4\sqrt3}{7-4\sqrt3}=\frac{5\times7-5\times4\times\sqrt3+3\times7\times\sqrt3-3\times4\times\sqrt3^2}{7^2-(4\sqrt3)^2}\\ =\frac{35-20\sqrt3+21\sqrt3-36}{49-48}\\ =\frac{\sqrt3-1}{1}\\ =\sqrt3-1$

Al igualar términos racionales e irracionales, obtenemos

$a+b\sqrt3=\sqrt3-1\\ =-1+1\sqrt3$

Por lo tanto, obtenemos a = -1, b = 1

(v) Sabemos que el factor de racionalización para $\sqrt{11}+\sqrt7\ is\ \sqrt{11}-\sqrt7$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{\sqrt{11}-\sqrt7}{\sqrt{11}+\sqrt7}\ by\ \sqrt{11}-\sqrt7$ , para obtener

$\frac{\sqrt{11}-\sqrt7}{\sqrt{11}+\sqrt7}\times\frac{\sqrt{11}-\sqrt7}{\sqrt{11}-\sqrt7}=\frac{\sqrt{11}^2+\sqrt7^2-2\times\sqrt{11}\times\sqrt7}{\sqrt{11}^2-\sqrt7^2}\\ =\frac{11+7-2\sqrt{77}}{11-7}\\ =\frac{18-2\sqrt{77}}{4}\\ =\frac{9}{2}-\frac{1}{2}\sqrt{77}$

Al igualar términos racionales e irracionales, obtenemos

$a-b\sqrt{77}=\frac{9}{2}-\frac{1}{2}\sqrt{77}$

Por lo tanto, obtenemos a = $\frac{9}{2}$ , b = $\frac{1}{2}$

(vi) Sabemos que el factor de racionalización para $4-3\sqrt5\ in\ 4+3\sqrt5$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{4+3\sqrt5}{4-3\sqrt5}\ by\ 4+3\sqrt5$ , para obtener

$\frac{4+3\sqrt5}{4-3\sqrt5}\times\frac{4+3\sqrt5}{4+3\sqrt5}=\frac{4^2+(3\sqrt5)^2+2\times4\times3\sqrt5}{4^2-(3\sqrt5)^2}\\ =\frac{16+45+24\sqrt5}{16-45}\\ =\frac{61+24\sqrt5}{-29}\\ =-\frac{61}{29}-\frac{24}{29}\sqrt5$

Al igualar términos racionales e irracionales, obtenemos

$a+b\sqrt5=-\frac{61}{29}-\frac{24}{29}\sqrt5$

Por lo tanto, obtenemos a = $-\frac{61}{29}$ , b = $-\frac{24}{29}$

Pregunta 7. Si 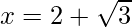$x=2+\sqrt3$ , encuentra el valor de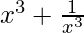 $x^3+\frac{1}{x^3}$

Solución:

$x^3+\frac{1}{x^3}=\left(x+\frac{1}{x}\right)\left(x^2-1+\frac{1}{x^2}\right)$ eso lo sabemos Tenemos que encontrar el valor de $x^3+\frac{1}{x^3}$

Como $x=2+\sqrt3$

Por lo tanto,

$\frac{1}{x}=\frac{1}{2+\sqrt3}$

Sabemos que el factor de racionalización para $2+\sqrt3\ is\ 2-\sqrt3$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{1}{2+\sqrt3}\ by\ 2-\sqrt3$

Llegar,

$\frac{1}{x}=\frac{1}{2+\sqrt3}\times\frac{2-\sqrt3}{2-\sqrt3}\\ =\frac{2-\sqrt3}{2^2-\sqrt3^2}\\ =\frac{2-\sqrt3}{4-3}\\ =2-\sqrt3$

Poniendo el valor de $x\ and\ \frac{1}{x}$ , obtenemos

$x^3+\frac{1}{x^3}=(2+\sqrt3+2-\sqrt3)((2+\sqrt3)^2-1+(2-\sqrt3)^2)\\ =4(2^2+(\sqrt3)^2+2\times2\times\sqrt3-1+2^2+(\sqrt3)^2-2\times2\times\sqrt3)\\ =4(4+3+4\sqrt3-1+4+3-4\sqrt3)\\ =52$

Por lo tanto, el valor de la expresión dada es 52.

Pregunta 8. Si 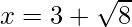$x=3+\sqrt8$ . Encuentre el valor de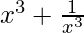 $x^3+\frac{1}{x^3}$

Solución:

$x^2+\frac{1}{x^2}=\left(x+\frac{1}{x}\right)^2-2$ eso lo sabemos Tenemos que encontrar el valor de $x^2+\frac{1}{x^2}\ as\ x=3+\sqrt8$

Por lo tanto,

$\frac{1}{x}=\frac{1}{3+\sqrt8}$

Sabemos que el factor de racionalización para $3+\sqrt8\ is\ 3-\sqrt8$ .

Multiplicaremos numerador y denominador de la expresión dada $\frac{1}{3+\sqrt8}\ by\ 3-\sqrt8$

Llegar,

$\frac{1}{x}=\frac{1}{3+\sqrt8}\times\frac{3-\sqrt8}{3-\sqrt8}\\ =\frac{3-\sqrt8}{3^2-\sqrt8^2}\\ =\frac{3-\sqrt8}{9-8}\\ =3-\sqrt8$

Poner el valor de $x\ and\ \frac{1}{x}$

Obtenemos,

$x^2+\frac{1}{x^2}=(3+\sqrt8+3-\sqrt8)^2-2\\ =(6)^2-2\\ =36-2\\ =34$

Por lo tanto, la expresión dada se simplifica a 34.

Pregunta 9. Halla el valor de 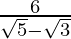$\frac{6}{\sqrt5-\sqrt3}$ , dado que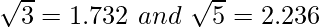 $\sqrt3=1.732\ and\ \sqrt5=2.236$

Solución:

Sabemos que para el factor de racionalización multiplicaremos el denominador y el numerador de la expresión dada $\frac{6}{\sqrt5-\sqrt3}\ by\ \sqrt5+\sqrt3$

Llegar,

$\frac{6}{\sqrt5-\sqrt3}\times\frac{\sqrt5+\sqrt3}{\sqrt5+\sqrt3}=\frac{6\sqrt5+6\sqrt3}{\sqrt5^2-\sqrt3^2}\\ =\frac{6\sqrt5+6\sqrt3}{5-3}\\ =\frac{6\sqrt5+6\sqrt3}{2}\\ =3\sqrt5+3\sqrt3$

Poner los valores de $\sqrt5\ and\ \sqrt3$

obtenemos,

$3\sqrt5+3\sqrt3=3(2.236)+3(1.732)\\ =6.708+5.196\\ =11.904$

Por lo tanto, el valor de la expresión dada es 11.904.

Pregunta 10. Encuentre el valor de cada uno de los siguientes con tres decimales, dado que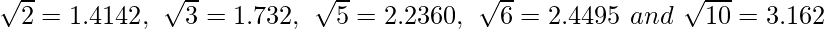 $\sqrt2=1.4142,\ \sqrt3=1.732,\ \sqrt5=2.2360,\ \sqrt6=2.4495\ and\ \sqrt{10}=3.162$

(i) $\frac{3-\sqrt5}{3+2\sqrt5}$

(ii) $\frac{1+\sqrt2}{3-2\sqrt2}$

Solución:

(i) Sabemos que el factor de racionalización para $3+2\sqrt5\ is\ 3-2\sqrt5$

Multiplicaremos numerador y denominador de la expresión dada $\frac{3-\sqrt5}{3+2\sqrt5}\ by\ 3-2\sqrt5$

Llegar

$\frac{3-\sqrt5}{3+2\sqrt5}\times\frac{3-2\sqrt5}{3-2\sqrt5}=\frac{3^2-3\times2\times\sqrt5-3\times\sqrt5+2\times\sqrt5^2}{3^2-(2\sqrt5)^2}\\ =\frac{9-9\sqrt5+10}{9-20}\\ =\frac{19-9\sqrt5}{-11}\\ =\frac{9\sqrt5-19}{11}$

Poner los valores de $\sqrt5$

Obtenemos

$\frac{9\sqrt5-19}{11}=\frac{9(2.236)-19}{11}\\ =\frac{20.124-19}{11}\\ =\frac{1.124}{11}\\ =0.102$

Por lo tanto, la expresión dada se simplifica a 0,102.

(ii) Sabemos que el factor de racionalización para $3-2\sqrt2\ is\ 3+2\sqrt2$

Multiplicaremos numerador y denominador de la expresión dada $\frac{1+\sqrt2}{3-2\sqrt2}\ by\ 3+2\sqrt2$

Llegar

$\frac{1+\sqrt2}{3-2\sqrt2}\times\frac{3+2\sqrt2}{3+2\sqrt2}=\frac{3+2\times\sqrt2+3\times\sqrt2+2\times\sqrt2^2}{3^2-(2\sqrt2)^2}\\ =\frac{3+2\sqrt2+3\sqrt2+4}{9-8}\\ =\frac{7+5\sqrt2}{1}\\ =7+5\sqrt2$

Poner los valores de $\sqrt2$

Obtenemos

$7+5\sqrt2=7+5(1.4142)\\ =7+7.071\\ =14.071$

Por lo tanto, la expresión dada se simplifica a 14.071.

Pregunta 11. Si 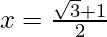$x=\frac{\sqrt3+1}{2}$ , encuentra el valor de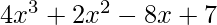 $4x^3+2x^2-8x+7$

Solución:

Tenemos, $x=\frac{\sqrt3+1}{2}$

Se puede simplificar como

$2x-1=\sqrt3$

Al elevar al cuadrado ambos lados, obtenemos

$(2x-1)^2=\sqrt3^2\\ (2x)^2+1-2\times2x=3\\ 4x^2+1-4x=3\\ 4x^2-4x-2=0$

La ecuación dada se puede reescribir como $4x^2+2x^2-8x+7=x(4x^2-4x-2)+\frac{6}{4}(4x^2-4x-2)+3+7$

Por lo tanto, tenemos

$4x^3+2x^2-8x+7=x(0)+\frac{6}{4}(0)+3+7\\ =3+7\\ =10$

Por lo tanto, el valor de la expresión dada es 10.

Publicación traducida automáticamente

Artículo escrito por yashkumar0457 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Clase 9 RD Sharma Solutions – Capítulo 3 Racionalización – Ejercicio 3.2 | conjunto 2

Pregunta 6. En cada uno de los siguientes determine los números racionales a y b:

Pregunta 7. Si $x=2+\sqrt3$ , encuentra el valor de $x^3+\frac{1}{x^3}$

Pregunta 8. Si $x=3+\sqrt8$ . Encuentre el valor de $x^3+\frac{1}{x^3}$

Pregunta 9. Halla el valor de $\frac{6}{\sqrt5-\sqrt3}$ , dado que $\sqrt3=1.732\ and\ \sqrt5=2.236$

Pregunta 10. Encuentre el valor de cada uno de los siguientes con tres decimales, dado que $\sqrt2=1.4142,\ \sqrt3=1.732,\ \sqrt5=2.2360,\ \sqrt6=2.4495\ and\ \sqrt{10}=3.162$

Pregunta 11. Si $x=\frac{\sqrt3+1}{2}$ , encuentra el valor de $4x^3+2x^2-8x+7$

Deja una respuesta Cancelar la respuesta

Pregunta 6. En cada uno de los siguientes determine los números racionales a y b:

Pregunta 7. Si , encuentra el valor de

Pregunta 8. Si . Encuentre el valor de

Pregunta 9. Halla el valor de , dado que

Pregunta 10. Encuentre el valor de cada uno de los siguientes con tres decimales, dado que

Pregunta 11. Si , encuentra el valor de

Deja una respuesta Cancelar la respuesta

Pregunta 7. Si $x=2+\sqrt3$ , encuentra el valor de $x^3+\frac{1}{x^3}$

Pregunta 8. Si $x=3+\sqrt8$ . Encuentre el valor de $x^3+\frac{1}{x^3}$

Pregunta 9. Halla el valor de $\frac{6}{\sqrt5-\sqrt3}$ , dado que $\sqrt3=1.732\ and\ \sqrt5=2.236$

Pregunta 10. Encuentre el valor de cada uno de los siguientes con tres decimales, dado que $\sqrt2=1.4142,\ \sqrt3=1.732,\ \sqrt5=2.2360,\ \sqrt6=2.4495\ and\ \sqrt{10}=3.162$

Pregunta 11. Si $x=\frac{\sqrt3+1}{2}$ , encuentra el valor de $4x^3+2x^2-8x+7$