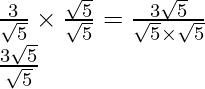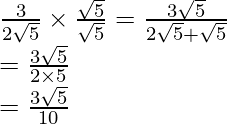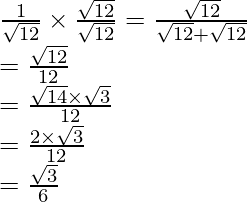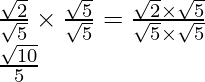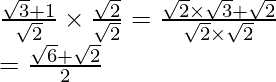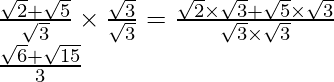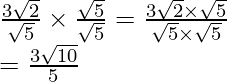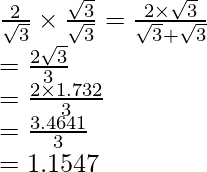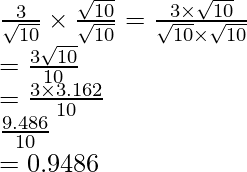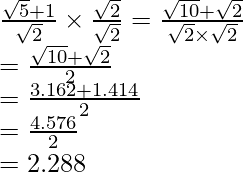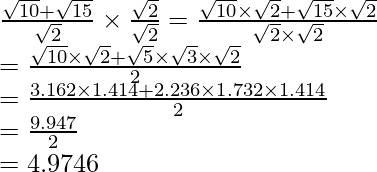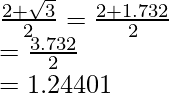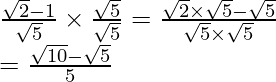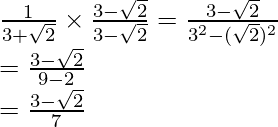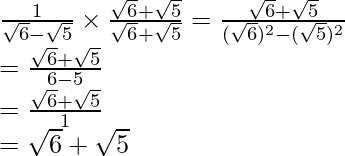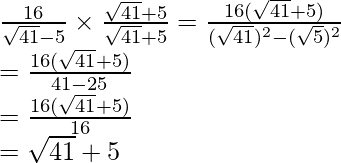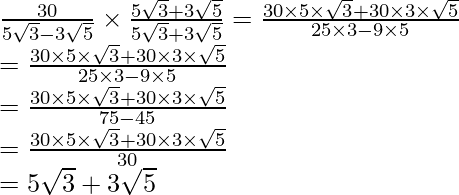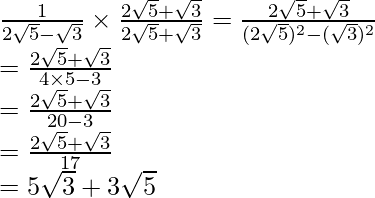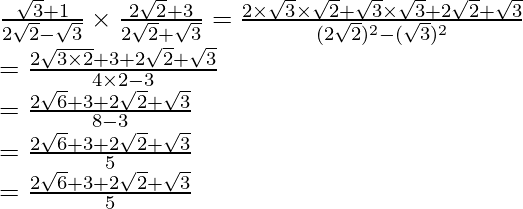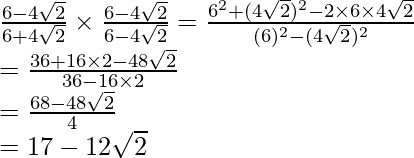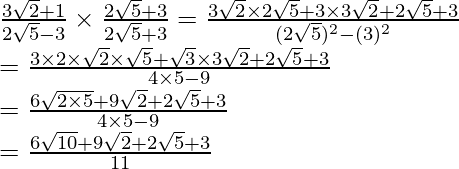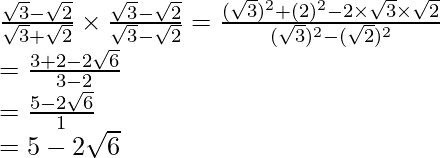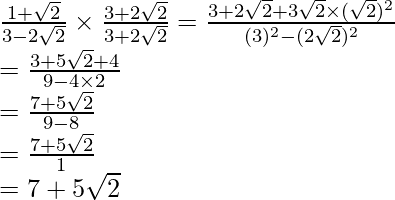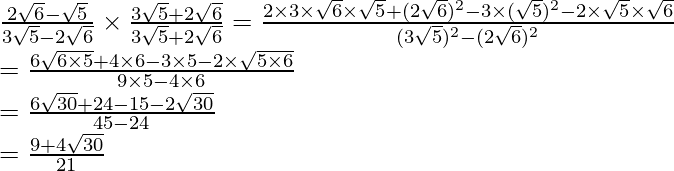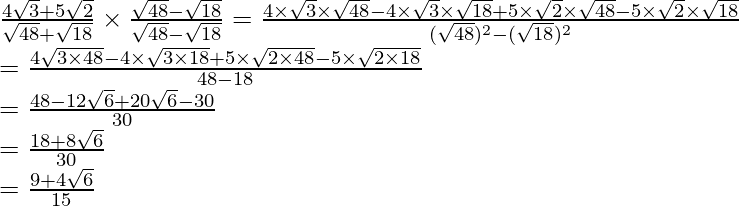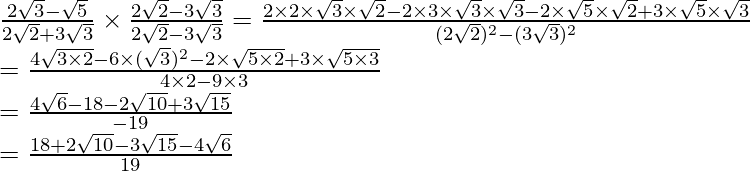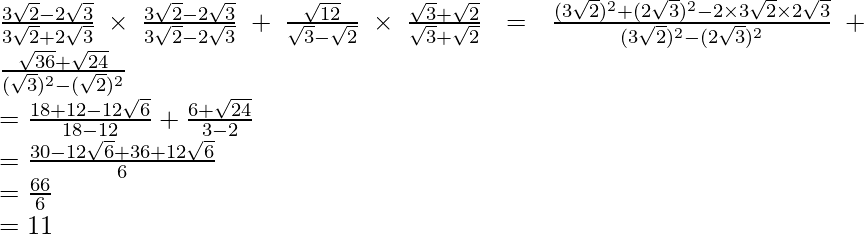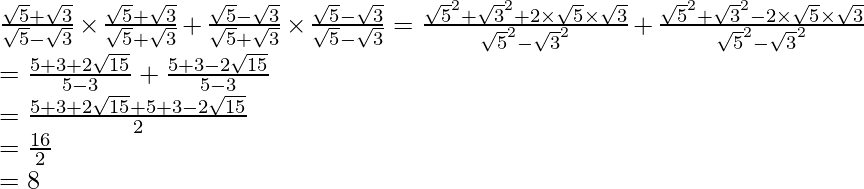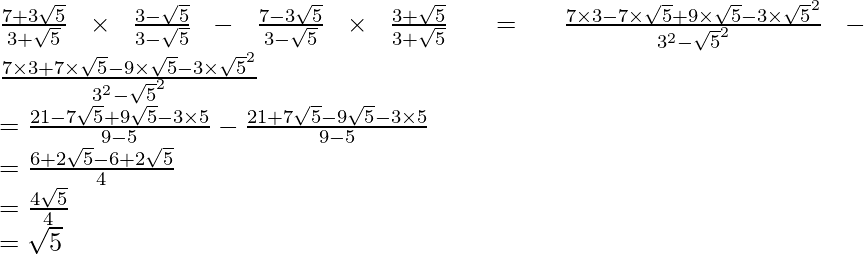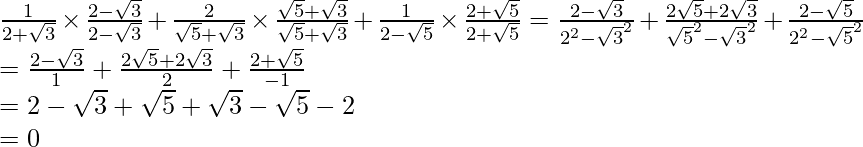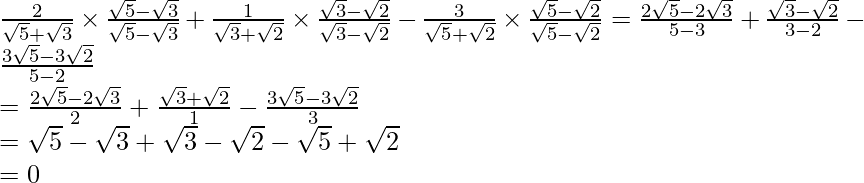Clase 9 RD Sharma Solutions – Capítulo 3 Racionalización – Ejercicio 3.2

Pregunta 1. Racionalizar el denominador de cada uno de los siguientes (i-vii):

(i) $\frac{3}{\sqrt5}$

(ii) $\frac{3}{2\sqrt5}$

(iii) $\frac{1}{\sqrt{12}}$

(iv) $\frac{\sqrt3}{\sqrt5}$

(v) $\frac{\sqrt3+1}{\sqrt2}$

(vi) $\frac{\sqrt2+\sqrt5}{3}$

(vii) $\frac{3\sqrt{2}}{\sqrt5}$

Solución:

(i) Sabemos que el factor de racionalización para $\frac{1}{\sqrt{a}}$ es $\sqrt{a}$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{3}{\sqrt5}$ por $\sqrt5$ . a

obtener $\frac{3}{\sqrt5}\times\frac{\sqrt5}{\sqrt5}=\frac{3\sqrt5}{\sqrt5\times\sqrt5}\\ \frac{3\sqrt5}{\sqrt5}$

Por lo tanto, la expresión dada se simplifica a $\frac{3\sqrt5}{5}$ .

(ii) Sabemos que el factor de racionalización para $\frac{1}{\sqrt{a}}$ es $\sqrt{a}$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{3}{2\sqrt5}$ por $\sqrt5$ . a

obtener $\frac{3}{2\sqrt5}\times\frac{\sqrt5}{\sqrt5}=\frac{3\sqrt5}{2\sqrt5+\sqrt5}\\ =\frac{3\sqrt5}{2\times5}\\ =\frac{3\sqrt5}{10}$

Por lo tanto, la expresión dada se simplifica a $\frac{3\sqrt5}{10}$

(iii) Sabemos que el factor de racionalización para $\frac{1}{\sqrt{a}}$ es $\sqrt{a}$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{1}{\sqrt{12}}$ por $\sqrt{12}$ .

Llegar $\frac{1}{\sqrt{12}}\times\frac{\sqrt{12}}{\sqrt{12}}=\frac{\sqrt{12}}{\sqrt{12}+\sqrt{12}}\\ =\frac{\sqrt{12}}{12}\\ =\frac{\sqrt{14}\times\sqrt3}{12}\\ =\frac{2\times\sqrt3}{12}\\ =\frac{\sqrt3}{6}$

Por lo tanto, la expresión dada se simplifica a $\frac{\sqrt3}{6}$

(iv) Sabemos que el factor de racionalización para $\frac{1}{\sqrt{a}}$ es $\sqrt{a}$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{\sqrt2}{\sqrt5}$ es $\sqrt5$ .

Llegar $\frac{\sqrt2}{\sqrt5}\times\frac{\sqrt5}{\sqrt5}=\frac{\sqrt2\times\sqrt5}{\sqrt5\times\sqrt5}\\ \frac{\sqrt{10}}{5}$

Por lo tanto, la expresión dada se simplifica a $\frac{\sqrt{10}}{5}$

(v) Sabemos que el factor de racionalización para $\frac{1}{\sqrt{a}}$ es $\sqrt{a}$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{\sqrt3+1}{\sqrt2}$ por $\sqrt2$ para obtener $\frac{\sqrt3+1}{\sqrt2}\times\frac{\sqrt2}{\sqrt2}=\frac{\sqrt2\times\sqrt3+\sqrt2}{\sqrt2\times\sqrt2}\\ =\frac{\sqrt6+\sqrt2}{2}$

Por lo tanto, la expresión dada se simplifica a $\frac{\sqrt6+\sqrt2}{2}$

(vi) Sabemos que el factor de racionalización para $\frac{1}{\sqrt{a}}$ es $\sqrt{a}$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{\sqrt2+\sqrt5}{\sqrt3}$ por $\sqrt3$ para obtener $\frac{\sqrt2+\sqrt5}{\sqrt3}\times\frac{\sqrt3}{\sqrt3}=\frac{\sqrt2\times\sqrt3+\sqrt5\times\sqrt3}{\sqrt3\times\sqrt3}\\ \frac{\sqrt6+\sqrt{15}}{3}$

Por lo tanto, la expresión dada se simplifica a $\frac{\sqrt6+\sqrt{15}}{3}$ .

(vii) Sabemos que el factor de racionalización para $\frac{1}{\sqrt{a}}$ es $\sqrt{a}$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{3\sqrt2}{\sqrt5}$ por $\sqrt5$ para obtener $\frac{3\sqrt2}{\sqrt5}\times\frac{\sqrt5}{\sqrt5}=\frac{3\sqrt2\times\sqrt5}{\sqrt5\times\sqrt5}\\ =\frac{3\sqrt{10}}{5}$

Por lo tanto, la expresión dada se simplifica a $\frac{3\sqrt{10}}{5}$

Pregunta 2. Encuentra el valor con tres decimales de cada uno de los siguientes. se da que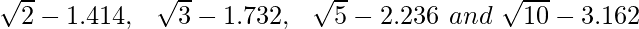 $\sqrt2-1.414,\ \ \sqrt3-1.732,\ \ \sqrt5-2.236\ and\ \sqrt{10}-3.162$

(i) $\frac{2}{\sqrt3}$

(ii) $\frac{3}{\sqrt{10}}$

(iii) $\frac{\sqrt5+1}{\sqrt2}$

(iv) $\frac{\sqrt{10}+\sqrt{15}}{\sqrt2}$

(v) $\frac{2+\sqrt3}{3}$

(vi) $\frac{\sqrt2-1}{\sqrt5}$

Solución:

(i) Sabemos que el factor de racionalización del denominador es $\sqrt3$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{2}{\sqrt3}$ por $\sqrt3$ para obtener

$\frac{2}{\sqrt3}\times\frac{\sqrt3}{\sqrt3}=\frac{2\times\sqrt3}{\sqrt3+\sqrt3}\\ =\frac{2\sqrt3}{3}\\ =\frac{2\times1.732}{3}\\ =\frac{3.4641}{3}\\ =1.1547$

El valor de la expresión 1,1547 se puede redondear a lugares decimales como 1,155.

Por lo tanto, la expresión dada se simplifica a 1.155.

(ii) Sabemos que el factor de racionalización del denominador es $\sqrt{10}$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{3}{\sqrt{10}}by\sqrt{10}$

Llegar

$\frac{3}{\sqrt{10}}\times\frac{\sqrt{10}}{\sqrt{10}}=\frac{3\times\sqrt{10}}{\sqrt{10}\times\sqrt{10}}\\ =\frac{3\sqrt{10}}{10}\\ =\frac{3\times3.162}{10}\\ \frac{9.486}{10}\\ =0.9486$

El valor de la expresión 0,9486 se puede redondear a decimales como 0,949.

Por lo tanto, la expresión dada se simplifica a 0,949.

(iii) Sabemos que el factor de racionalización del denominador es $\sqrt2$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{\sqrt5+1}{\sqrt2}$ por $\sqrt2$

Llegar

$\frac{\sqrt5+1}{\sqrt2}\times\frac{\sqrt2}{\sqrt2}=\frac{\sqrt{10}+\sqrt2}{\sqrt2\times\sqrt2}\\ =\frac{\sqrt{10}+\sqrt2}{2}\\ =\frac{3.162+1.414}{2}\\ =\frac{4.576}{2}\\ =2.288$

El valor de la expresión 2,288 se puede redondear a lugares decimales como 2,288.

Por lo tanto, la expresión dada se simplifica a 2.288.

(iv) Sabemos que el factor de racionalización del denominador es $\sqrt2$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{\sqrt{10}+\sqrt{15}}{\sqrt2}$

por $\sqrt2$ conseguir

$\frac{\sqrt{10}+\sqrt{15}}{\sqrt2}\times\frac{\sqrt2}{\sqrt2}=\frac{\sqrt{10}\times\sqrt2+\sqrt{15}\times\sqrt2}{\sqrt2\times\sqrt2}\\ =\frac{\sqrt{10}\times\sqrt2+\sqrt5\times\sqrt3\times\sqrt2}{2}\\ =\frac{3.162\times1.414+2.236\times1.732\times1.414}{2}\\ =\frac{9.947}{2}\\ =4.9746$

El valor de la expresión 4,9746 se puede redondear a decimales como 4,975.

Por lo tanto, la expresión dada se simplifica a 4,975.

(v) Sabemos que el factor de racionalización del denominador es $\sqrt3$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{2+\sqrt3}{2}by\sqrt3$ para obtener

$\frac{2+\sqrt3}{2}=\frac{2+1.732}{2}\\ =\frac{3.732}{2}\\ =1.24401$

El valor de la expresión 1,24401 se puede redondear a decimales como 1,244.

Por lo tanto, la expresión dada se simplifica a 1,244.

(vi) Sabemos que el factor de racionalización del denominador es $\sqrt5$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{\sqrt2-1}{\sqrt5}by \sqrt5$

Llegar

$\frac{\sqrt2-1}{\sqrt5}\times\frac{\sqrt5}{\sqrt5}=\frac{\sqrt2\times\sqrt5-\sqrt5}{\sqrt5\times\sqrt5}\\ =\frac{\sqrt{10}-\sqrt5}{5}$

Poniendo el valor de $\sqrt{10}$ y $\sqrt5$ , obtenemos

El valor de la expresión 0,1852 se puede redondear a decimales como 0,185.

Por lo tanto, la expresión dada se simplifica a 0.185

Pregunta 3. Exprese cada uno de los siguientes con denominador racional:

(i) $\frac{1}{3+\sqrt2}$

(ii) $\frac{1}{\sqrt6-\sqrt5}$

(iii) $\frac{16}{\sqrt{41}-5}$

(iv) $\frac{30}{5\sqrt3-3\sqrt5}$

(v) $\frac{1}{2\sqrt5-\sqrt3}$

(vi) $\frac{\sqrt3+1}{2\sqrt2-\sqrt3}$

(vii) $\frac{6-4\sqrt2}{6+4\sqrt2}$

(viii) $\frac{3\sqrt2+1}{2\sqrt5-3}$

(ix) $\frac{b^2}{\sqrt{a^2+b^2}+a^2}$

Solución:

(i) Sabemos que el factor de racionalización para $3+\sqrt2$ es $3-\sqrt2$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{1}{3+\sqrt2}by3-\sqrt2$ para obtener

$\frac{1}{3+\sqrt2}\times\frac{3-\sqrt2}{3-\sqrt2}=\frac{3-\sqrt2}{3^2-(\sqrt2)^2}\\ =\frac{3-\sqrt2}{9-2}\\ =\frac{3-\sqrt2}{7}$

Por lo tanto, la expresión dada se simplifica con denominador racional a $\frac{3-\sqrt2}{7}$

(ii) Sabemos que el factor de racionalización para $\sqrt6-\sqrt5$ es $\sqrt6+\sqrt5$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{1}{\sqrt6-\sqrt5}$ por $\sqrt6+\sqrt5$

Llegar

$\frac{1}{\sqrt6-\sqrt5}\times\frac{\sqrt6+\sqrt5}{\sqrt6+\sqrt5}=\frac{\sqrt6+\sqrt5}{(\sqrt6)^2-(\sqrt5)^2}\\ =\frac{\sqrt6+\sqrt5}{6-5}\\ =\frac{\sqrt6+\sqrt5}{1}\\ =\sqrt6+\sqrt5$

Por lo tanto, la expresión dada se simplifica con denominador racional a $\sqrt6+\sqrt5$

(iii) Sabemos que el factor de racionalización para $\sqrt{41}-5$ es $\sqrt{41}+5$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{16}{\sqrt{41}-5}$ por $\sqrt{41}+5$

Llegar

$\frac{16}{\sqrt{41}-5}\times\frac{\sqrt{41}+5}{\sqrt{41}+5}=\frac{16(\sqrt{41}+5)}{(\sqrt{41})^2-(\sqrt{5})^2}\\ =\frac{16(\sqrt{41}+5)}{41-25}\\ =\frac{16(\sqrt{41}+5)}{16}\\ =\sqrt{41}+5$

Por lo tanto, la expresión dada se simplifica con denominador racional a $\sqrt{41}+5$

(iv) Sabemos que el factor de racionalización para $5\sqrt3-3\sqrt5$ es $5\sqrt3+3\sqrt5$ . Multiplicaremos numerador y denominador de la expresión dada $\frac{30}{5\sqrt3-3\sqrt5}$ por $5\sqrt3+3\sqrt5$

Llegar

$\frac{30}{5\sqrt3-3\sqrt5}\times\frac{5\sqrt3+3\sqrt5}{5\sqrt3+3\sqrt5}=\frac{30\times5\times\sqrt3+30\times3\times\sqrt5}{25\times3-9\times5}\\ =\frac{30\times5\times\sqrt3+30\times3\times\sqrt5}{25\times3-9\times5}\\ =\frac{30\times5\times\sqrt3+30\times3\times\sqrt5}{75-45}\\ =\frac{30\times5\times\sqrt3+30\times3\times\sqrt5}{30}\\ =5\sqrt3+3\sqrt5$

Por lo tanto, la expresión dada se simplifica con denominador racional a $5\sqrt3+3\sqrt5$

(v) Sabemos que el factor de racionalización para es . Multiplicaremos el numerador y el denominador de la expresión dada por para obtener

$\frac{1}{2\sqrt5-\sqrt3}\times\frac{2\sqrt5+\sqrt3}{2\sqrt5+\sqrt3}=\frac{2\sqrt5+\sqrt3}{(2\sqrt5)^2-(\sqrt3)^2}\\ =\frac{2\sqrt5+\sqrt3}{4\times5-3}\\ =\frac{2\sqrt5+\sqrt3}{20-3}\\ =\frac{2\sqrt5+\sqrt3}{17}\\ =5\sqrt3+3\sqrt5$

Por lo tanto, la expresión dada se simplifica con denominador racional a $\frac{2\sqrt5+\sqrt3}{17}$

(vi) Sabemos que el factor de racionalización para $2\sqrt2-\sqrt3is2\sqrt2+\sqrt3$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{\sqrt3+1}{2\sqrt2-\sqrt3}$ por $2\sqrt2+\sqrt3$ para obtener

$\frac{\sqrt3+1}{2\sqrt2-\sqrt3}\times\frac{2\sqrt2+3}{2\sqrt2+\sqrt3}=\frac{2\times\sqrt3\times\sqrt2+\sqrt3\times\sqrt3+2\sqrt2+\sqrt3}{(2\sqrt2)^2-(\sqrt3)^2}\\ =\frac{2\sqrt{3\times2}+3+2\sqrt2+\sqrt3}{4\times2-3}\\ =\frac{2\sqrt6+3+2\sqrt2+\sqrt3}{8-3}\\ =\frac{2\sqrt6+3+2\sqrt2+\sqrt3}{5}\\ =\frac{2\sqrt6+3+2\sqrt2+\sqrt3}{5}$

Por lo tanto, la expresión dada se simplifica con denominador racional a = $\frac{2\sqrt6+3+2\sqrt2+\sqrt3}{5}$

(vii) Sabemos que el factor de racionalización para $6+4\sqrt2is6-4\sqrt2$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{6-4\sqrt2}{6+4\sqrt2}$ por $6-4\sqrt2$ para obtener

$\frac{6-4\sqrt2}{6+4\sqrt2}\times\frac{6-4\sqrt2}{6-4\sqrt2}=\frac{6^2+(4\sqrt2)^2-2\times6\times4\sqrt2}{(6)^2-(4\sqrt2)^2}\\ =\frac{36+16\times2-48\sqrt2}{36-16\times2}\\ =\frac{68-48\sqrt2}{4}\\ =17-12\sqrt2$

Por lo tanto, la expresión dada se simplifica con denominador racional a $17-12\sqrt2$

(viii) Sabemos que el factor de racionalización para $2\sqrt5-3$ es $2\sqrt5+3$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{3\sqrt2+1}{2\sqrt5-3}by2\sqrt5+3$ para obtener

$\frac{3\sqrt2+1}{2\sqrt5-3}\times\frac{2\sqrt5+3}{2\sqrt5+3}=\frac{3\sqrt2\times2\sqrt5+3\times3\sqrt2+2\sqrt5+3}{(2\sqrt5)^2-(3)^2}\\ =\frac{3\times2\times\sqrt2\times\sqrt5+\sqrt3\times3\sqrt2+2\sqrt5+3}{4\times5-9}\\ =\frac{6\sqrt{2\times5}+9\sqrt2+2\sqrt5+3}{4\times5-9}\\ =\frac{6\sqrt{10}+9\sqrt2+2\sqrt5+3}{11}$

Por lo tanto, la expresión dada se simplifica con denominador racional a $\frac{6\sqrt{10}+9\sqrt2+2\sqrt5+3}{11}$

(ix) Sabemos que el factor de racionalización para $\sqrt{a^2+b^2}+a$ es $\sqrt{a^2+b^2}-a$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{b^2}{\sqrt{a^2+b^2}+a}$ por $\sqrt{a^2+b^2}-a$ para obtener

$\frac{b^2}{\sqrt{a^2+b^2}+a}\times\frac{\sqrt{a^2+b^2}-a}{\sqrt{a^2+b^2}-a}=\frac{b^2(\sqrt{a^2+b^2-a)}}{(\sqrt{a^2+b^2})^2-a^2}\\ =\frac{b^2(\sqrt{a^2+b^2}-a)}{a^2+b^2-a}\\ =\frac{b^2(\sqrt{a^2+b^2}-a)}{b^2}\\ =\sqrt{a^2+b^2}-a$

Por lo tanto, la expresión dada se simplifica con denominador racional a $\sqrt{a^2+b^2}-a$

Pregunta 4. Justifica el denominador y simplifica:

(i) $\frac{3-\sqrt2}{3+\sqrt2}$

(ii) $\frac{5+2\sqrt3}{7+4\sqrt3}$

(iii) $\frac{1+\sqrt2}{3-2\sqrt2}$

(iv) $\frac{2\sqrt6-\sqrt5}{3\sqrt5-2\sqrt6}$

(v) $\frac{4\sqrt3+5\sqrt2}{\sqrt{48}+\sqrt{18}}$

(vi) $\frac{2\sqrt3-\sqrt5}{2\sqrt2+3\sqrt3}$

Solución:

(i) Sabemos que el factor de racionalización para $\sqrt3+\sqrt2$ es $\sqrt3-\sqrt2$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{\sqrt3-\sqrt2}{\sqrt3+\sqrt2}$ por $\sqrt3-\sqrt2$ para obtener

$\frac{\sqrt3-\sqrt2}{\sqrt3+\sqrt2}\times\frac{\sqrt3-\sqrt2}{\sqrt3-\sqrt2}=\frac{(\sqrt3)^2+(2)^2-2\times\sqrt3\times\sqrt2}{(\sqrt3)^2-(\sqrt2)^2}\\ =\frac{3+2-2\sqrt6}{3-2}\\ =\frac{5-2\sqrt6}{1}\\ =5-2\sqrt6$

Por lo tanto, la expresión dada se simplifica a $5-2\sqrt6$ .

(ii) Sabemos que el factor de racionalización para $7+4\sqrt3$ es $7-4\sqrt3$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{5+2\sqrt3}{7+4\sqrt3}$ por $7-4\sqrt3$ para obtener

$\frac{5+2\sqrt3}{7+4\sqrt3}\times\frac{7-4\sqrt3}{7-4\sqrt3}=\frac{5\times7-5\times4\sqrt3+2\times7\times\sqrt3-2\times4\times(\sqrt3)^2}{(7)^2-(4\sqrt3)^2}\\ =\frac{35-20\sqrt3+14\sqrt3-8\times3}{49-48}\\ =\frac{11-6\sqrt3}{1}\\ =11-6\sqrt3$

Por lo tanto, la expresión dada se simplifica a $11-6\sqrt3$ .

(iii) Sabemos que el factor de racionalización para $3-2\sqrt2$ es $3+2\sqrt2$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{1+\sqrt2}{3-2\sqrt2}$ por $3+2\sqrt2$ para obtener

$\frac{1+\sqrt2}{3-2\sqrt2}\times\frac{3+2\sqrt2}{3+2\sqrt2}=\frac{3+2\sqrt2+3\sqrt2\times(\sqrt2)^2}{(3)^2-(2\sqrt2)^2}\\ =\frac{3+5\sqrt2+4}{9-4\times2}\\ =\frac{7+5\sqrt2}{9-8}\\ =\frac{7+5\sqrt2}{1}\\ =7+5\sqrt2$

Por lo tanto, la expresión dada se simplifica a $7+5\sqrt2$ .

(iv) Sabemos que el factor de racionalización para $3\sqrt5-2\sqrt6$ es $3\sqrt5+2\sqrt6$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{2\sqrt6-\sqrt5}{3\sqrt5-2\sqrt6}$ por $3\sqrt5+2\sqrt6$ para obtener

$\frac{2\sqrt6-\sqrt5}{3\sqrt5-2\sqrt6}\times\frac{3\sqrt5+2\sqrt6}{3\sqrt5+2\sqrt6}=\frac{2\times3\times\sqrt6\times\sqrt5+(2\sqrt6)^2-3\times(\sqrt5)^2-2\times\sqrt5\times\sqrt6}{(3\sqrt5)^2-(2\sqrt6)^2}\\ =\frac{6\sqrt{6\times5}+4\times6-3\times5-2\times\sqrt{5\times6}}{9\times5-4\times6}\\ =\frac{6\sqrt{30}+24-15-2\sqrt{30}}{45-24}\\ =\frac{9+4\sqrt{30}}{21}$

Por lo tanto, la expresión dada se simplifica a $\frac{9+4\sqrt{30}}{21}$ .

(v) Sabemos que el factor de racionalización para $\sqrt{48}+\sqrt{18}is\sqrt{48}-\sqrt{18}$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{4\sqrt3+5\sqrt2}{\sqrt{48}+\sqrt{18}}$ por $\sqrt{48}-\sqrt{18}$ para obtener

$\frac{4\sqrt3+5\sqrt2}{\sqrt{48}+\sqrt{18}}\times\frac{\sqrt{48}-\sqrt{18}}{\sqrt{48}-\sqrt{18}}=\frac{4\times\sqrt3\times\sqrt{48}-4\times\sqrt3\times\sqrt{18}+5\times\sqrt2\times\sqrt{48}-5\times\sqrt2\times\sqrt{18}}{(\sqrt{48})^2-(\sqrt{18})^2}\\ =\frac{4\sqrt{3\times48}-4\times\sqrt{3\times18}+5\times\sqrt{2\times48}-5\times\sqrt{2\times18}}{48-18}\\ =\frac{48-12\sqrt6+20\sqrt6-30}{30}\\ =\frac{18+8\sqrt6}{30}\\ =\frac{9+4\sqrt6}{15}$

Por lo tanto, la expresión dada se simplifica a $\frac{9+4\sqrt6}{15}$ .

(vi) Sabemos que el factor de racionalización para $2\sqrt2+3\sqrt3$ es $2\sqrt2-3\sqrt3$ . Multiplicaremos el numerador y el denominador de la expresión dada $\frac{2\sqrt3-\sqrt5}{2\sqrt2+3\sqrt3}by2\sqrt2-3\sqrt3$ para obtener

$\frac{2\sqrt3-\sqrt5}{2\sqrt2+3\sqrt3}\times\frac{2\sqrt2-3\sqrt3}{2\sqrt2-3\sqrt3}=\frac{2\times2\times\sqrt3\times\sqrt2-2\times3\times\sqrt3\times\sqrt3-2\times\sqrt5\times\sqrt2+3\times\sqrt5\times\sqrt3}{(2\sqrt2)^2-(3\sqrt3)^2}\\ =\frac{4\sqrt{3\times2}-6\times(\sqrt3)^2-2\times\sqrt{5\times2}+3\times\sqrt{5\times3}}{4\times2-9\times3}\\ =\frac{4\sqrt6-18-2\sqrt{10}+3\sqrt{15}}{-19}\\ =\frac{18+2\sqrt{10}-3\sqrt{15}-4\sqrt6}{19}$

Por lo tanto, la expresión dada se simplifica a $\frac{18+2\sqrt{10}-3\sqrt{15}-4\sqrt6}{19}$ .

Pregunta 5. Simplifica:

(i) $\frac{3\sqrt2-2\sqrt3}{3\sqrt2+2\sqrt3}+\frac{\sqrt{12}}{\sqrt3-\sqrt2}\\$

(ii) $\frac{5+\sqrt3}{5-\sqrt3}+\frac{5-\sqrt3}{5+\sqrt3}$

(iii) $\frac{7+3\sqrt5}{3+\sqrt5}+\frac{7-3\sqrt5}{3-\sqrt5}$

(iv) $\frac{1}{2+\sqrt3}+\frac{2}{\sqrt5-\sqrt3}+\frac{1}{2-\sqrt5}$

(v) $\frac{2}{\sqrt5+\sqrt3}+\frac{1}{\sqrt3+\sqrt2}+\frac{3}{\sqrt5+\sqrt2}$

Solución:

(i) Sabemos que el factor de racionalización para $3\sqrt2+2\sqrt3$ y $\sqrt3-\sqrt2$ son $3\sqrt2-2\sqrt3$ y $\sqrt3+\sqrt2$ respectivamente.

Multiplicaremos numerador y denominador de la expresión dada $\frac{3\sqrt2-2\sqrt3}{3\sqrt2+2\sqrt3}\ and\ \frac{\sqrt{12}}{\sqrt3-\sqrt2}\ by\ 3\sqrt2-2\sqrt3\ and\ \sqrt3+\sqrt2$ respectivamente, para obtener

$\frac{3\sqrt2-2\sqrt3}{3\sqrt2+2\sqrt3}\times\frac{3\sqrt2-2\sqrt3}{3\sqrt2-2\sqrt3}+\frac{\sqrt{12}}{\sqrt3-\sqrt2}\times\frac{\sqrt3+\sqrt2}{\sqrt3+\sqrt2}=\frac{(3\sqrt2)^2+(2\sqrt3)^2-2\times3\sqrt2\times2\sqrt3}{(3\sqrt2)^2-(2\sqrt3)^2}+\frac{\sqrt{36}+\sqrt{24}}{(\sqrt3)^2-(\sqrt2)^2}\\ =\frac{18+12-12\sqrt6}{18-12}+\frac{6+\sqrt{24}}{3-2}\\ =\frac{30-12\sqrt6+36+12\sqrt6}{6}\\ =\frac{66}{6}\\ =11$

Por lo tanto, la expresión dada se simplifica a 11.

(ii) Sabemos que el factor de racionalización para $\sqrt5-\sqrt3\ and\ \sqrt5+\sqrt3\ are\ \sqrt5+\sqrt3\ and\ \sqrt5-\sqrt3$ respectivamente.

Multiplicaremos numerador y denominador de la expresión dada $\frac{\sqrt5+\sqrt3}{\sqrt5-\sqrt3}\ and\ \frac{\sqrt5-\sqrt3}{\sqrt5+\sqrt3}\ by\ \sqrt5+\sqrt3\ and\ \sqrt5+\sqrt3$ respectivamente, para obtener

$\frac{\sqrt5+\sqrt3}{\sqrt5-\sqrt3}\times\frac{\sqrt5+\sqrt3}{\sqrt5+\sqrt3}+\frac{\sqrt5-\sqrt3}{\sqrt5+\sqrt3}\times\frac{\sqrt5-\sqrt3}{\sqrt5-\sqrt3}=\frac{\sqrt5^2+\sqrt3^2+2\times\sqrt5\times\sqrt3}{\sqrt5^2-\sqrt3^2}+\frac{\sqrt5^2+\sqrt3^2-2\times\sqrt5\times\sqrt3}{\sqrt5^2-\sqrt3^2}\\ =\frac{5+3+2\sqrt{15}}{5-3}+\frac{5+3-2\sqrt{15}}{5-3}\\ =\frac{5+3+2\sqrt{15}+5+3-2\sqrt{15}}{2}\\ =\frac{16}{2}\\ =8$

Por lo tanto, la expresión dada se simplifica a 8.

(iii) Sabemos que el factor de racionalización para $3+\sqrt5\ and\ 3-\sqrt5\ are\ 3-\sqrt5\ and\ 3+\sqrt5$ respectivamente.

Multiplicaremos numerador y denominador de la expresión dada $\frac{7+3\sqrt5}{3+\sqrt5}\ and\ \frac{7-3\sqrt5}{3-\sqrt5}\ by\ 3-\sqrt5\ and\ 3+\sqrt5$ respectivamente, para obtener

$\frac{7+3\sqrt5}{3+\sqrt5}\times\frac{3-\sqrt5}{3-\sqrt5}-\frac{7-3\sqrt5}{3-\sqrt5}\times\frac{3+\sqrt5}{3+\sqrt5}=\frac{7\times3-7\times\sqrt5+9\times\sqrt5-3\times\sqrt5^2}{3^2-\sqrt5^2}-\frac{7\times3+7\times\sqrt5-9\times\sqrt5-3\times\sqrt5^2}{3^2-\sqrt5^2}\\ =\frac{21-7\sqrt5+9\sqrt5-3\times5}{9-5}-\frac{21+7\sqrt5-9\sqrt5-3\times5}{9-5}\\ =\frac{6+2\sqrt5-6+2\sqrt5}{4}\\ =\frac{4\sqrt5}{4}\\ =\sqrt5$

Por lo tanto, la expresión dada se simplifica a $\sqrt5$ .

(iv) Sabemos que el factor de racionalización para $2+\sqrt3,\ \sqrt5-\sqrt3\ and\ 2-\sqrt5\ are\ 2-\sqrt3,\ \sqrt5+\sqrt3\ and\ 2+\sqrt5$ respectivamente.

Multiplicaremos numerador y denominador de la expresión dada $\frac{1}{2+\sqrt3},\ \frac{2}{\sqrt5-\sqrt3}\ and\ \frac{1}{2-\sqrt5}\ by\ 2-\sqrt3,\ \sqrt5+\sqrt3\ and\ 2+\sqrt5$ respectivamente, para obtener

$\frac{1}{2+\sqrt3}\times\frac{2-\sqrt3}{2-\sqrt3}+\frac{2}{\sqrt5+\sqrt3}\times\frac{\sqrt5+\sqrt3}{\sqrt5+\sqrt3}+\frac{1}{2-\sqrt5}\times\frac{2+\sqrt5}{2+\sqrt5}=\frac{2-\sqrt3}{2^2-\sqrt3^2}+\frac{2\sqrt5+2\sqrt3}{\sqrt5^2-\sqrt3^2}+\frac{2-\sqrt5}{2^2-\sqrt5^2}\\ =\frac{2-\sqrt3}{1}+\frac{2\sqrt5+2\sqrt3}{2}+\frac{2+\sqrt5}{-1}\\ =2-\sqrt3+\sqrt5+\sqrt3-\sqrt5-2\\ =0$

Por lo tanto, la expresión dada se simplifica a 0.

(v) Sabemos que el factor de racionalización para $\sqrt5+\sqrt3,\ \sqrt3+\sqrt2\ and\ \sqrt5+\sqrt2\ are\ \sqrt5-\sqrt3,\ \sqrt3-\sqrt2\ and\ \sqrt5-\sqrt2$ respectivamente.

Multiplicaremos numerador y denominador de la expresión dada $\frac{2}{\sqrt5+\sqrt3},\ \frac{1}{\sqrt3+\sqrt2}\ and\ \frac{3}{\sqrt5+\sqrt2}\ by\ 2-\sqrt3,\ \sqrt5+\sqrt3\ and\ 2+\sqrt5$ respectivamente, para obtener

$\frac{2}{\sqrt5+\sqrt3}\times\frac{\sqrt5-\sqrt3}{\sqrt5-\sqrt3}+\frac{1}{\sqrt3+\sqrt2}\times\frac{\sqrt3-\sqrt2}{\sqrt3-\sqrt2}-\frac{3}{\sqrt5+\sqrt2}\times\frac{\sqrt5-\sqrt2}{\sqrt5-\sqrt2}=\frac{2\sqrt5-2\sqrt3}{5-3}+\frac{\sqrt3-\sqrt2}{3-2}-\frac{3\sqrt5-3\sqrt2}{5-2}\\ =\frac{2\sqrt5-2\sqrt3}{2}+\frac{\sqrt3+\sqrt2}{1}-\frac{3\sqrt5-3\sqrt2}{3}\\ =\sqrt5-\sqrt3+\sqrt3-\sqrt2-\sqrt5+\sqrt2\\ =0$

Por lo tanto, la expresión dada se simplifica a 0.