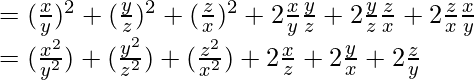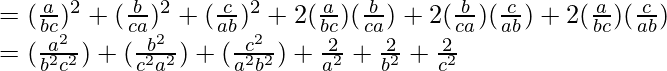Pregunta 1: Escribe lo siguiente en forma desarrollada:
(yo) (a + 2b + c) 2
(ii) (2a − 3b − c) 2
(iii) (−3x+y+z) 2
(iv) (m+2n−5p) 2
(v) (2+x−2y) 2
(vi) (a 2 +b 2 +c 2 ) 2
(vii) (ab+bc+ca) 2
(viii) (x/y+y/z+z/x) 2
(ix) (a/bc + b/ac + c/ab) 2
(x) (x+2y+4z) 2
(xi) (2x−y+z) 2
(xii) (−2x+3y+2z) 2
Solución:
Siguiendo la identidad,
(x + y + z) 2 = x 2 + y 2 + z 2 + 2xy + 2yz + 2xz
(yo) (a + 2b + c) 2
= a 2 + (2b) 2 + c 2 + 2a(2b) + 2ac + 2(2b)c
= a 2 + 4b 2 + c 2 + 4ab + 2ac + 4bc
(ii) (2a − 3b − c) 2
= [(2a) + (−3b) + (−c)] 2
= (2a) 2 + (−3b) 2 + (−c) 2 + 2(2a)(−3b) + 2(−3b)(−c) + 2(2a)(−c)
= 4a 2 + 9b 2 + c 2 − 12ab + 6bc − 4ca
(iii) (−3x+y+z) 2
= [(−3x) 2 + y 2 + z 2 + 2(−3x)y + 2yz + 2(−3x)z]
= 9x 2 + y 2 + z 2 − 6xy + 2yz − 6xz
(iv) (m+2n−5p) 2
= metro 2 + (2n) 2 + (−5p) 2 + 2m × 2n + (2×2n×−5p) + 2m × (−5p)
= metro 2 + 4n 2 + 25p 2 + 4mn − 20np − 22:00
(v) (2+x−2y) 2
= 2 2 + x 2 + (−2y) 2 + 2(2)(x) + 2(x)(−2y) + 2(2)(−2y)
= 4 + x 2 + 4y 2 + 4 x − 4xy − 8y
(vi) (a 2 +b 2 +c 2 ) 2
= (a 2 ) 2 + (b 2 ) 2 + (c 2 ) 2 + 2a 2 b 2 + 2b 2 c 2 + 2a 2 c 2
= un 4 + segundo 4 + do 4 + 2a 2 segundo 2 + 2b 2 do 2 + 2c 2 un 2
(vii) (ab+bc+ca) 2
= (ab) 2 + (bc) 2 + (ca) 2 + 2(ab)(bc) + 2(bc)(ca) + 2(ab)(ca)
= a 2 b 2 + b 2 c 2 + c 2 a 2 + 2(ac)b 2 + 2(ab)(c) 2 + 2(bc)(a) 2
(viii) (x/y+y/z+z/x) 2
(ix) (a/bc + b/ac + c/ab) 2
(x) (x+2y+4z) 2
= x 2 + (2y) 2 + (4z) 2 + (2x)(2y) + 2(2y)(4z) + 2x(4z)
= x2 + 4y2 + 16z2 + 4xy + 16yz + 8xz
(xi) (2x−y+z) 2
= (2x) 2 + (−y) 2 + (z) 2 + 2(2x)(−y) + 2(−y)(z) + 2(2x)(z)
= 4x 2 + y 2 + z 2 − 4xy − 2yz + 4xz
(xii) (−2x+3y+2z) 2
= (−2x) 2 + (3y) 2 + ( 2z) 2 + 2(−2x)(3y) + 2(3y)(2z) + 2(−2x)(2z)
= 4x 2 + 9y 2 + 4z 2 −12xy + 12yz −8xz
Pregunta 2: simplificar
(i) (a + b + c) 2 + (a – b + c) 2
(ii) (a + b + c) 2 − (a − b + c) 2
(iii) (a + b + c) 2 + (a – b + c) 2 + (a + b – c) 2
(iv) (2x + pag – c) 2 – (2x – pag + c) 2
(v) (x 2 + y 2 – z 2 ) 2 – (x 2 – y 2 + z 2 ) 2
Solución:
(i) (a + b + c) 2 + (a – b + c) 2
= (a 2 + b 2 + c 2 + 2ab+2bc+2ca) + (a 2 + (−b) 2 + c 2 −2ab−2bc+2ca)
= 2a 2 + 2b 2 + 2c 2 + 4ca
(ii) (a + b + c) 2 − (a − b + c) 2
= (a 2 + b 2 + c 2 + 2ab+2bc+2ca) − (a 2 + (−b) 2 + c 2 −2ab−2bc+2ca)
= a2 + b2 + c2 + 2ab + 2bc + 2ca − a2 − b2 − c2 + 2ab + 2bc − 2ca
= 4ab + 4bc
(iii) (a + b + c) 2 + (a – b + c) 2 + (a + b – c)
= a 2 + b 2 + c 2 + 2ab + 2bc + 2ca + (a 2 + b 2 + (c) 2 − 2ab − 2cb + 2ca) + (a 2 + b 2 + c 2 + 2ab − 2bc – 2ca )
= 3a 2 + 3b 2 + 3c 2 + 2ab − 2bc + 2ca
(iv) (2x + pag – c) 2 – (2x – pag + c) 2
= [4x 2 + p 2 + c 2 + 4xp − 2pc − 4xc] − [4x 2 + p 2 + c 2 − 4xp− 2pc + 4xc]
= 4x 2 + pag 2 + c 2 + 4xp − 2pc − 4cx − 4x 2 − pag 2 − c 2 + 4xp + 2pc− 4cx
= 8xp − 8xc
= 8(xp − xc)
(v) (x 2 + y 2 – z 2 ) 2 – (x 2 – y 2 + z 2 ) 2
= (x 2 + y 2 + (−z) 2 ) 2 − (x 2 − y 2 + z 2 ) 2
= [x 4 + y 4 + z 4 + 2x2y 2 – 2y2z 2 – 2x2z 2 − [x 4 + y 4 + z 4 − 2x2y 2 − 2y2z 2 + 2x2z 2 ]
= 4x 2 y 2 – 4z 2 x 2
Pregunta 3: Si a + b + c = 0 y a 2 + b 2 + c 2 = 16, encuentre el valor de ab + bc + ca.
Solución:
Dado,
a + b + c = 0 y a 2 + b 2 + c 2 = 16
Elija a + b + c = 0
Cuadrando ambos lados,
(a + b + c) 2 = 0
a 2 + b 2 + c 2 + 2 (ab + bc + ca) = 0
16 + 2(ab + bc + c) = 0
2(ab + bc + ca) = -16
ab + bc + ca = -16/2 = -8
o
ab + bc + ca = -8
Publicación traducida automáticamente
Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA